Sprache der Funktionen

Lernpfad

Funktion - eine eindeutige Zuordnung

1. Einführung von Funktionen
2. Funktion - eine eindeutige Zuordnung
3. Sprache der Funktionen

Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben.

• Die Funktionen-Sprache kennen und anwenden können.
• Die Funktionen-Sprache in Anwendungsbeispiele interpretieren können.
• Formeln im Hinblick auf funktionale Aspekte untersuchen können.
• Definitions- und Wertemenge einer Funktion bestimmen können.

• FA 1.4: Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im Kontext deuten können.
• FA 1.7: Funktionen als mathematische Modelle verstehen und damit verständig arbeiten können.

Um den "Gültigkeitsbereich" einer Funktion anzugeben, verwendet man folgende Begriffe:

Definitions- und Wertemenge

Alle Werte, die die unabhängige Variable (Argument) annimmt, bilden zusammen die Definitionsmenge D der Funktion. Alle Werte, die die abhängige Variable annimmt, bilden die Wertemenge W

Bezeichnungen bei Funktionen

• Die Elemente der Definitionsmenge D einer Funktion nennt man Argumente oder Stellen der Funktion.
• Die Elemente der Wertemenge W nennt man Funktionswerte der Funktion.
• f(x) ist der Funktionswert der Funktion f an der Stelle x.
• Der Graph der Funktion f besteht aus den Punkten (x / f(x)).

Funktionenschreibweise

• Funktion $f: \mathbb{N}\ \rightarrow \mathbb{Z}$ mit $f(x) = 2x - 3$ ist eine normalerweise verwendete Funktionsschreibweise.
• Auch $f: \mathbb{N} \rightarrow \mathbb{Z}$mit $y = 2x - 3$ ist üblich.
• "f" ist der Funktionsname. Für den Funktionsnamen verwendet man üblicherweise (nicht zwingend) Kleinbuchstaben.
• "2x - 3" ist der Funktionsterm der Funktion f.
• Die Schreibweise $\mathbb{N\rightarrow} \mathbb{Z}$ legt für die Funktion f als Grundmenge $\mathbb{N}$ und als Zielmenge $\mathbb{Z}$ fest. Die Zielmenge gibt an, in welcher Menge die Funktionswerte der Funktion f liegen können. Die Wertemenge ist immer eine Teilmenge der Zielmenge. Die Grundmenge gibt an, in welcher Menge die Argumente der Funktion f liegen können. Die Definitionsmenge ist immer Teilmenge der Grundmenge.
• Ist die Definitionsmenge und Wertemenge einer Funktion eine Teilmenge von $\mathbb{R}$ so spricht man von einer reellen Funktion. Wenn nicht anders angegeben, handelt es sich um reelle Funktionen.

Musterbeispiel

Bestimme die Definitions- und die Wertemenge der Funktion näherungsweise:

1. 

1. 

Lösung

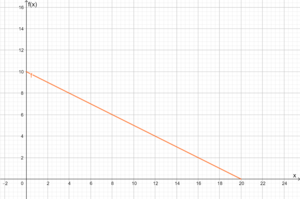
1. D = [0 ; 20] W = [0 ; 10]
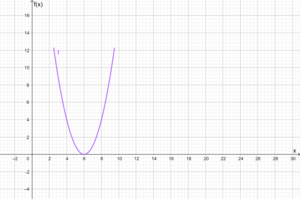
2. D = [2,5 ; 9,5] W = [0 ; 12,1]

Übung

Bestimme die Definitions- und die Wertemenge der Funktion näherungsweise: 

1. 

1. 

Lösung

1. $D =$ [-2 ; 6] $W =$ [4]
2. $D =$[-1,5;0,8] $W =$ [-0,2 ; 2,6]

Siehe auch

• Vorlage:Show-Hide (in englischer Sprache)

Zusammenfassung

Im folgenden Video wird der Inhalt dieses Lernpfades noch einmal zusammengefasst. Schau es dir aufmerksam an! Wenn dir einzelne Inhalte noch nicht ganz klar sind, dann gehe zurück in den betreffenden Teil des Lernpfades!

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

zurück