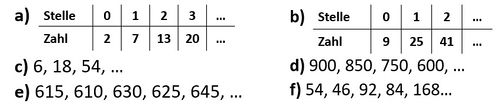Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Benutzer:Elena Jedtke/Tests: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=== Probleme mit der Mathe-Umgebung === | === Probleme mit der Mathe-Umgebung === | ||
{{Box| 1=Übung: Aufgabe 7 - Regelmäßigkeiten erkennen und fortsetzen| | |||
2=[[Datei:Zahlenfolgen.jpg|500px|zentriert]] | |||
'''Bearbeite diese Aufgabe in deinem Hefter!''' | |||
'''a)''' Beschreibe jeweils die Regelmäßigkeiten in den Zahlenfolgen mit einem Satz und setze die Zahlenfolgen um drei Zahlen fort. | |||
'''b)''' Schreibe einen Term mit "x" für die Zahlenfolge (2) auf. Erkläre, warum du für die anderen Zahlenfolgen keinen solchen Term aufstellen kannst. | |||
'''c)''' Schreibe eine Zahlenfolge für den Term <math> 16 + 8 \cdot x </math> auf. | |||
|Üben}} | |||
<math>x_1,2</math> | |||
<span style="color: blue">'''b)''' Gegeben sind die beiden Geraden <math>f(x)=4x-5</math> und <math>g(x)=-3x+9</math>.</span> | <span style="color: blue">'''b)''' Gegeben sind die beiden Geraden <math>f(x)=4x-5</math> und <math>g(x)=-3x+9</math>.</span> | ||
Aktuelle Version vom 17. Mai 2020, 09:11 Uhr
Probleme mit der Mathe-Umgebung
Üben
Bearbeite diese Aufgabe in deinem Hefter!
a) Beschreibe jeweils die Regelmäßigkeiten in den Zahlenfolgen mit einem Satz und setze die Zahlenfolgen um drei Zahlen fort.
b) Schreibe einen Term mit "x" für die Zahlenfolge (2) auf. Erkläre, warum du für die anderen Zahlenfolgen keinen solchen Term aufstellen kannst.
c) Schreibe eine Zahlenfolge für den Term auf.
b) Gegeben sind die beiden Geraden und .
Der Schnittpunkt liegt bei x= 2 und y = 3. Wie komme ich zu meiner Lösung? Ich setze die beiden Funktionen und gleich. Dann erhalte ich .Dann löse ich nach x auf. Ich erhalte den Wert x = 2. Jetzt kann ich den Wert x=2 in eine der beiden Gleichungen einsetzen und den y-Wert berechnen
c) Gegeben sind die beiden Geraden und .
Der Schnittpunkt liegt bei x= 20 und y = 27. Wie komme ich zu meiner Lösung? Ich setze die beiden Funktionen und gleich. Dann erhalte ich . Nun löse ich nach x auf. Ich erhalte den Wert x = 20. Jetzt kann ich den Wert x=20 in eine der beiden Gleichungen einsetzen und den y-Wert berechnen.