Einführung in die Automatentheorie/2. Stunde: Unterschied zwischen den Versionen
K (11 Versionen importiert) |
(formatiert) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 166: | Zeile 166: | ||
{{Fortsetzung|weiter=weiter mit der 3. Stunde|weiterlink=Einführung in die Automatentheorie/3. Stunde}} | |||
{{Einführung in die Automatentheorie}} | |||
Aktuelle Version vom 10. August 2019, 12:51 Uhr
Zustände und Übergänge
Automaten kann man sich als eine Art "Maschine" vorstellen, die stur einem festgelegtem Schema folgt, so wie zum Beispiel eine Kaffeemaschine. Eine Kaffeemaschine kann sich in verschiedenen Zuständen befinden (warten, Kaffe kochen, Kaffee warm halten). Das festgelegte Schema sagt ihr, dass sie, wenn sie angeschaltet wird, Kaffee kochen soll. Wenn sie damit fertig ist, soll sie den Kaffee warm halten, solange, bis sie ausgeschaltet wird.
Im Allgemeinen haben alle Automaten ein solches festes vorgegebenes Schema wie eine Kaffeemaschine.
Wie wir bereits gesehen haben, setzt sich ein Automat aus Zuständen und Übergängen zusammen. Ein festgelegtes Schema gibt vor, wann ein Automat von einem Zustand in einen anderen übergeht.
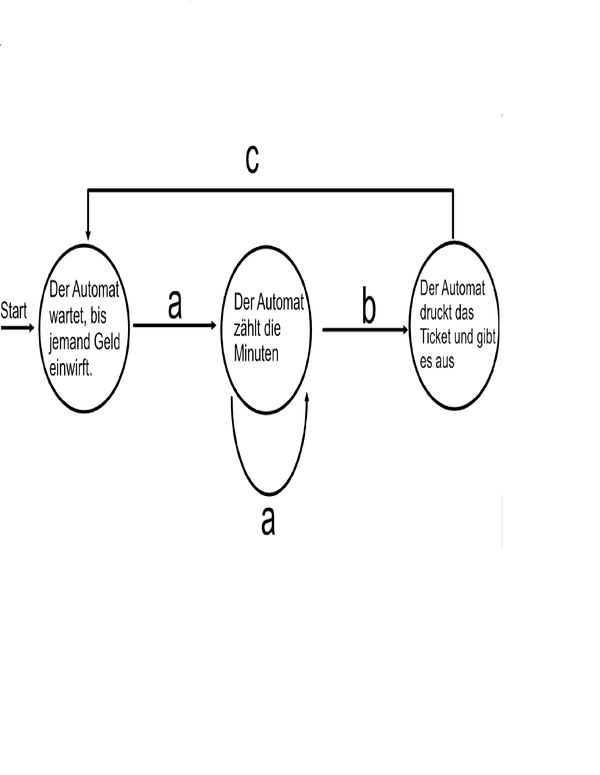
Schauen wir uns hierzu nochmal den Parkscheinautomat an.
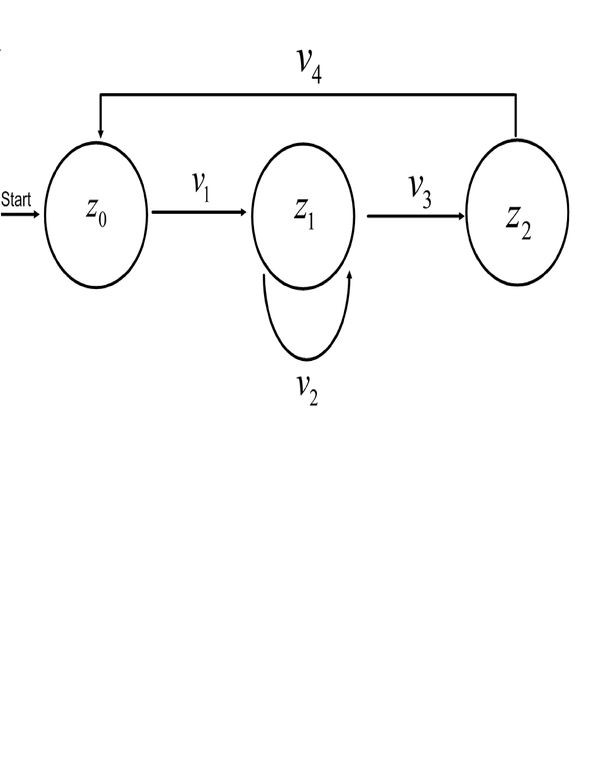
Beschriften wir die Zustände und Übergänge ein wenig anders, sieht das ganze so aus:
Dieser Automat hat folgende Zustände:
- z0: Der Automat wartet auf eine Eingabe. Wartezustnd
- z1: Der Automat merkt sich, wie viel Geld eingeworfen wurde.
- z2: Der Automat druckt das Parkticket und gibt es aus.
Außerdem hat der Automat folgende Übergänge:
- v1: Geld wird eingeworfen.
=> Der Automat wechselt von z0 nach z1.
- v2: Es wird mehr Geld eingeworfen.
=> Der Automat bleibt in z1 und zählt die Minuten.
- v3: Der Knopf "Parkschein ausgeben" wird gedrückt.
=> Der Automat wechselt in z2.
- v4: Der Parkschein wird entnommen.
=> Der Automat wechselt zurück in den Zustand z0.
Diese Abstraktion hat den Vorteil, dass nun eine gewisse Vergleichbarkeit mit anderen Automaten geschaffen wird und so generelle Aussagen und allgemeine Betrachtungen möglich sind.
Eine einfache Supermarktkasse funktioniert folgendermaßen:
- Wird ein Preis eingegeben, addiert die Kasse diesem zum Gesamtpreis.
- Drückt jemand auf die Taste "Kassieren", wird der Gesamtpreis angezeigt und die Geldlade geöffnet.
- Wird die Geldlade geschlossen, wartet die Kasse darauf, dass erneut ein Preis eingegeben wird.
| z0 | Die Kasse wartet auf die Eingabe eines Preises | |
| z1 | Ein Preis wurde eingegeben | und der Knopf "Kassieren" wurde allerdings noch nicht gedrückt |
| z2 | Der Gesamtpreis wird angezeigt | und die Geldlade ist geöffnet |
| v1 | Der erste Preis eines Artikels wird eingegeben | |
| v2 | Ein weiterer Preis wird eingeben | |
| v3 | Der Knopf "Kassieren" wird gedrückt | |
| v4 | Die Geldlade wird geschlossen |
Besondere Zustände
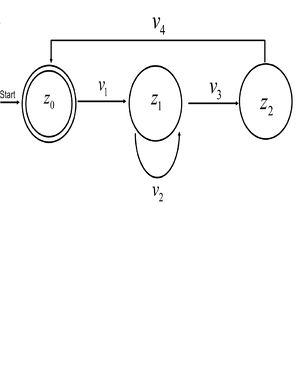
Auf den Zustand mit dem Startpfeil sind wir ja schon eingegangen, dieser Zustand heißt Startzustand.
Jeder andere Zustand hat noch einen anderen "besonderen" Zustand, einen Endzustand. der Endzustand wird im Allgemeinen durch einen doppelten Kreis gekennzeichnet. Ein Automat kann auch mehrere Endzustände haben. Dazu aber später mehr.
In unserem Beispiel ist der Startzustand gleich dem Endzustand.
Eingaben
Ein Automat reagiert auf Aktionen. So wechselt der Parkscheinautomat zum Beispiel beim Einwurf von einer Geldmünze den Zustand. Eine Folge von Aktionen wird Eingabe genannt. So ist z.B. [20 ct - 10ct - 10ct - 20ct - Tickettaste drücken - Ticket entnehmen] eine Eingabe.
Ein Automat verarbeitet eine Eingabe, indem er die einzelnen Aktionen der Reihe nach betrachtet und entsprechend reagiert.
Reagieren heißt hier:
Der Automat sucht einen Übergang, der vom aktuellen Zustand ausgeht und mit der Aktion, die an der Reihe ist, beschriftet ist.
Eingaben können unterschiedlich aussehen, es können sowohl Folgen von Zahlen, Wörtern, Zeichen oder Buchstaben sein. Bei realen Automaten sind dies Knöpfe, Münzen, Auswahltasten usw.
Um Automaten strukturiert und übersichtlich darstellen zu können, verwendet man oft Kürzel an den Übergängen. Diese Standardisierung ermöglicht uns außerdem die Analyse der Eigenschaften von Automaten.
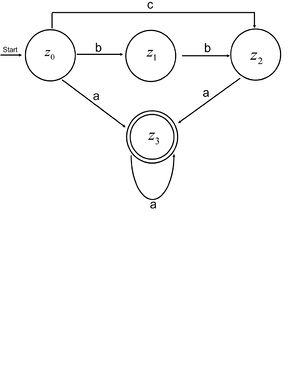
Betrachte folgenden Automaten.
Fülle den Lückentext aus.
Start bei z0.
Wechsel von z0 nach z2 mit c.
Wechsel von z2 nach z3 mit a.
Der Automat bleibt im Zustand z3 mit a.
Nach der Eingabe caa befindet sich der Automat also in Zustand z3.
Die Eingabe bbb hingegen kann der Automat nicht verarbeiten, da es vom Zustand z2 aus keinen Übergang gibt, der mit b markiert ist.
Betrachte den Automaten aus Aufgabe 2.2.
Gegeben sind verschiedene Eingaben. Setze in die entsprechenden Lücken die passenden Zustände ein (z.B. "z0-z1-z2" oder schreibe "kein Endzustand". Du must deine Antwort genau so eingeben wie hier im Beispiel, nur ohne die Anführungszeichen).
Wie bereits erwähnt, können Eingaben sehr unterschiedlich sein. Deswegen ist es nötig, zu jedem Automaten anzugeben, aus welchen "Buchstaben" die "Sprache" besteht, die er versteht.
Die Menge dieser "Buchstaben" wird Eingabealphabet genannt. So ist das Eingabealphabet des Automaten aus dem Beispiel oben {a,b,c}.
Das Eingabealphabet muss natürlich nicht aus wirklichen Buchstaben bestehen, es kann genauso aus den ganzen Wörtern, Sätzen oder Zahlen bestehen.
Übungsaufgaben