Benutzer:BirgitLachner/Vorrangregel entdecken: Unterschied zwischen den Versionen
Benutzer:BirgitLachner/Vorrangregel entdecken
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 1: | Zeile 1: | ||
Das Rechnen mit großen Zahlen sollte für dich hoffentlich kein Problem mehr darstellen. Und auch mehrere Rechnungen, die hintereinander ausgeführt werden müssen, solltest du schon ein wenig Erfahrung haben. Aber schau dir mal die folgenden Rechnungen an … das ist schon heftig, oder? | Das Rechnen mit großen Zahlen sollte für dich hoffentlich kein Problem mehr darstellen. Und auch mehrere Rechnungen, die hintereinander ausgeführt werden müssen, solltest du schon ein wenig Erfahrung haben. Aber schau dir mal die folgenden Rechnungen an … das ist schon heftig, oder? | ||
<center>[[Screenshot 20190302 180628.png]]</center> | <center>[[Datei:Screenshot 20190302 180628.png|400px]]</center> | ||
Da sind so viele Rechnungen mit Plus, Minus und auch Mal hintereinander, da weiß man gar nicht, so man anfangen soll? Oder fängt man einfach von vorne an? Oder gibt es eine Rechnung in der langen Rechnung, mit der man am besten anfängt, weil dann alles folgende einfacher wird? | Da sind so viele Rechnungen mit Plus, Minus und auch Mal hintereinander, da weiß man gar nicht, so man anfangen soll? Oder fängt man einfach von vorne an? Oder gibt es eine Rechnung in der langen Rechnung, mit der man am besten anfängt, weil dann alles folgende einfacher wird? | ||
Version vom 25. Juni 2019, 09:54 Uhr
Das Rechnen mit großen Zahlen sollte für dich hoffentlich kein Problem mehr darstellen. Und auch mehrere Rechnungen, die hintereinander ausgeführt werden müssen, solltest du schon ein wenig Erfahrung haben. Aber schau dir mal die folgenden Rechnungen an … das ist schon heftig, oder?
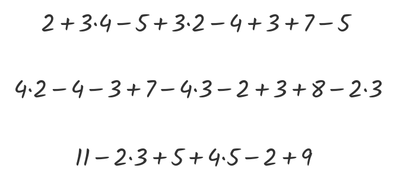
Da sind so viele Rechnungen mit Plus, Minus und auch Mal hintereinander, da weiß man gar nicht, so man anfangen soll? Oder fängt man einfach von vorne an? Oder gibt es eine Rechnung in der langen Rechnung, mit der man am besten anfängt, weil dann alles folgende einfacher wird?
Das zu erforschen, soll nun deine Aufgabe sein.
Als Forschungs-Hilfsmittel, soll dir das Programm GraspableMath dienen. Der Name kommt vom englischen Verb „to grasp“ = greifen. Dabei geht es unter anderem darum Mathematik begrifen zu können indem man es angreift. Was mit dem angreifen gemeint ist, wird im folgenden Abschnitt anhand von kurzen Filmsequenzen erklärt.
