Beschreibende Statistik/Einsatz des Taschenrechners/ausführliche Anleitung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
main>Nina Krämer
Keine Bearbeitungszusammenfassung
(f)
Markierung: 2017-Quelltext-Bearbeitung
 
(19 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
Zunächst müssen die Daten erfasst werden.
Zunächst müssen die Daten erfasst werden. Dann kann gerechnet werden.
== Datenerfassung ==


Dabei ist zwischen Beobachtungswerten und Merkmalsausprägungen mit zugehörigen Häufigkeiten zu unterscheiden.
Dabei ist zwischen Beobachtungswerten und Merkmalsausprägungen mit zugehörigen Häufigkeiten zu unterscheiden.


1. Schritt:
=== Auswahl zwischen Urliste und Häufigkeitsverteilung ===
2. Schritt:
3. Schritt:
4. Schritt:
5. Schritt:
6. Schritt:
7. Schritt:
8. Schritt:
Urliste
Häufigkeitsverteilung


Berechnungen
Diese Einstellung nimmt man über {{Vorlage:Taste|⇧ Shift}} {{Vorlage:Taste|MODE}} vor:


Über SHIFT und 1 gelangt man in das Statistik-Menü:
<!-- Tabelle SHIFT MODE -->
{|"class=wikitable"
|-
|1: Mth2D || || 2: Linear
|-
|3: Deg || || 4: ln X
|-
|5: Gra || || 6: Fix
|-
|7: Sci || || 8: Norm
|}
<!-- Ende Tabelle SHIFT MODE -->


== Stichprobenumfang <math>n</math> ==
Dann {{Vorlage:Taste|↓}} wählen und man gelangt zu:
Wählt man 4 erhält man


Wählt man 1 und = erhält man bei absoluter Häufigkeitsverteilung den Stichprobenumfang.
<!-- Tabelle SHIFT MODE nach unten -->
Mit AC beenden. Über SHIFT und 1 neue Größe berechnen.
{|"class=wikitable"
|-
|1: ab/c || || 2: v
|-
|3: CMPLX || || 4: STAT
|-
|5: PerD || || 6: AbAut
|-
|7: ←KNTR→ || ||
|}
<!-- Ende Tabelle SHIFT MODE nach unten-->


== Artihmetisches Mittel <math>\bar x</math> ==
Hier wählt man {{Vorlage:Taste|4}} für STAT und erhält:


Wählt man 4 erhält man
<!-- Tabelle Häufigkeit -->
{|"class=wikitable"
|-
| colspan="2"| Häufigkeit?
|-
|1: EIN || || 2: AUS
|}
<!-- Ende Häufigkeit -->


Man wählt
* {{Vorlage:Taste|1}} für die Eingabe absoluter oder relativer Häufigkeitsverteilungen oder
* {{Vorlage:Taste|2}} für die Eingabe von Beobachtungswerten aus einer Urliste.


=== Dateneingabe ===
Über {{Vorlage:Taste|MODE}} gelangt man ins das folgende Menü:


Wählt man 2 und = erhält man das arithmetische Mittel.
<!-- Tabelle MODE -->
Mit AC beenden. Über SHIFT und 1 neue Größe berechnen.
{|"class=wikitable"
|-
|1: COMP || || 2: STAT
|-
|3: TABLE || || 4: DIST
|-
|5: EQN || || 6: MATRIX
|-
|7: INEQ || || 8: VECTOR
|}
<!-- Ende Tabelle MODE -->


== Standardabweichung <math>\sigma</math> ==
Man wählt {{Vorlage:Taste|2}} für STAT:
Wählt man 4 erhält man


<!-- Tabelle MODE 2 -->
{|"class=wikitable"
|-
|1: 1-VAR || || 2: A+BX
|-
|3: _+cX<sup>2</sup> || || 4: ln X
|-
|5: e^X || || 6: A <math>\cdot</math> B^X
|-
|7: A <math>\cdot</math> X^B || || 8: 1/X
|}
<!-- Ende Tabelle MODE 2 -->


{{Vorlage:Taste|1}} für 1-VAR (Häufigkeit für eine Variable) eingeben, liefert:


Wählt man 3 und = erhält man die Standardabweichung.
<!-- Tabelle Urliste oder Häufigkeit -->
Mit AC beenden. Über SHIFT und 1 neue Größe berechnen.
{|"class=wikitable"
|-
|Eingabe einer Urliste || || Eingabe einer Häufigkeitsverteilung
|-
|(Häufigkeit? AUS) || || (Häufigkeit ? EIN)
|-
|[[Datei:TR Urliste.PNG|Urliste]] || || [[Datei:TR Häufigkeit.PNG|Häufigkeiten]]
|}
<!-- Ende Tabelle MODE 2 -->


== Summe der Beobachtungswerte ==
==== Eingabe einer Urliste ====
Wählt man 3 erhält man:


Jetzt werden nacheinander die Beobachtungswerte eingegeben, wobei jeder einzelne Wert mit {{Vorlage:Taste|&#61;}}  zu bestätigen ist.
Das Ende der Eingabe erfolgt über {{Vorlage:Taste|AC}}.
==== Eingabe einer Häufigkeitsverteilung ====
Jetzt werden nacheinander die Merkmalsausprägungen eingegeben, wobei jeder einzelne Wert mit {{Vorlage:Taste|&#61;}} zu bestätigen ist.
Dann {{Vorlage:Taste|↓}} und {{Vorlage:Taste|→}} zur Spalte FREQ wechseln und hier die zugehörige Häufigkeit (absolut oder relativ) erfassen.
Das Ende der Eingabe erfolgt über {{Vorlage:Taste|AC}} .
== Berechnungen ==
Über {{Vorlage:Taste|⇧&nbsp;Shift}} und {{Vorlage:Taste|1}} gelangt man in das Statistik-Menü:
{|class="wikitable
|-
| 1: Type || || 2: Data
|-
| 3: Sum || || 4: Var
|-
|5: Distr || || 6: MinMax
|}
=== Stichprobenumfang <math>n</math> ===
Wählt man {{Vorlage:Taste|4}} erhält man:
<!-- Tabelle Menü 4 -->
{|class="wikitable
|-
| 1: <math>n</math> || || 2: <math>\bar x</math>
|-
| 3: <math>\sigma x</math> || || 4: <math>sx</math>
|}
<!-- Ende Tabelle Menü 4 -->
Wählt man {{Vorlage:Taste|1}} und  {{Vorlage:Taste|&#61;}}  erhält man bei absoluter Häufigkeitsverteilung den Stichprobenumfang.
Mit {{Vorlage:Taste|AC}} beenden.
Über {{Vorlage:Taste|⇧&nbsp;Shift}} und  {{Vorlage:Taste|1}}  neue Größe berechnen.
=== Artihmetisches Mittel <math>\bar x</math> ===
Wählt man {{Vorlage:Taste|4}} erhält man
<!-- Tabelle Menü 4 -->
{|class="wikitable
|-
| 1: <math>n</math> || || 2: <math>\bar x</math>
|-
| 3: <math>\sigma x</math> || || 4: <math>sx</math>
|}
<!-- Ende Tabelle Menü 4 -->
Wählt man {{Vorlage:Taste|2}} und {{Vorlage:Taste|&#61;}}  erhält man das arithmetische Mittel.
Mit <span style="background:yellow">AC</span> beenden.
Über <span style="background:yellow">SHIFT</span> und <span style="background:yellow">1</span> neue Größe berechnen.
=== Standardabweichung <math>\sigma</math> ===
Wählt man <span style="background:yellow">4</span> erhält man
<!-- Tabelle Menü 4 -->
{|class="wikitable
|-
| 1: <math>n</math> || || 2: <math>\bar x</math>
|-
| 3: <math>\sigma x</math> || || 4: <math>sx</math>
|}
<!-- Ende Tabelle Menü 4 -->
Wählt man <span style="background:yellow">3</span> und <span style="background:yellow">=</span> erhält man die Standardabweichung.
Mit <span style="background:yellow">AC</span> beenden.
Über <span style="background:yellow">SHIFT</span> und <span style="background:yellow">1</span> neue Größe berechnen.
=== Summe der Beobachtungswerte ===
Wählt man <span style="background:yellow">3</span> erhält man:
<!-- Tabelle Menü 3 -->
{|class="wikitable
|-
| 1: <math>\Sigma x^2</math> || || 2: <math>\Sigma x</math>
|}
<!-- Ende Tabelle Menü 3 -->
Mit <span style="background:yellow">2</span> und <span style="background:yellow">=</span> erhält man das gewünschte Ergebnis.


Mit 2 und = erhält man das gewünschte Ergebnis.
Bei Beobachtungswerten erhält man:
Bei Beobachtungswerten erhält man:
<math>\sum{i=1}^n a_i</math>
 
<math>\sum_{i=1}^n a_i</math>


Bei einer Häufigkeitsverteilung erhält man:
Bei einer Häufigkeitsverteilung erhält man:
<math>\sum{i=1}^k x_i \cdot H(x_i)=\sum{i=1}^k x_i \cdot H_i</math>
 
<math>\sum_{i=1}^k x_i \cdot H(x_i)=\sum_{i=1}^k x_i \cdot H_i</math>


bzw.
bzw.
<math>\sum{i=1}^k x_i \cdot h(x_i)=\sum{i=1}^k x_i \cdot h_i</math>


== Kleinster Beobachtungswerte <math>x_{Min}</math> ==
<math>\sum_{i=1}^k x_i \cdot h(x_i)=\sum_{i=1}^k x_i \cdot h_i</math>
Wählt man 6 erhält man:
 
Mit <span style="background:yellow">AC</span> beenden.
 
Über <span style="background:yellow">SHIFT</span> und <span style="background:yellow">1</span> neue Größe berechnen.
 
=== Kleinster Beobachtungswerte <math>x_{Min}</math> ===
Wählt man <span style="background:yellow">6</span> erhält man:
 
<!-- Tabelle Menü 6 -->
{|class="wikitable
|-
| 1: min<math>X</math> || || 2: max<math>X</math>
|-
| 3: Q1 || || 4: med
|-
| 5: Q2
|}
<!-- Ende Tabelle Menü 6 -->
 
Mit <span style="background:yellow">1</span> und <span style="background:yellow">=</span> erhält man den kleinsten Beobachtungswert.
 
Mit <span style="background:yellow">AC</span> beenden.
 
Über <span style="background:yellow">SHIFT</span> und <span style="background:yellow">1</span> neue Größe berechnen.
 
=== Größter Beobachtungswerte <math>x_{Max}</math> ===
Wählt man <span style="background:yellow">6</span> erhält man:
 
<!-- Tabelle Menü 6 -->
{|class="wikitable
|-
| 1: min<math>X</math> || || 2: max<math>X</math>
|-
| 3: Q1 || || 4: med
|-
| 5: Q2
|}
<!-- Ende Tabelle Menü 6 -->
 
 
Mit <span style="background:yellow">2</span> und <span style="background:yellow">=</span> erhält man den größten Beobachtungswert.
 
Mit <span style="background:yellow">AC</span> beenden.
 
Über <span style="background:yellow">SHIFT</span> und <span style="background:yellow">1</span> neue Größe berechnen.
 
=== Median <math>x_{Med}</math> ===
Wählt man <span style="background:yellow">6</span> erhält man:
 
<!-- Tabelle Menü 6 -->
{|class="wikitable
|-
| 1: min<math>X</math> || || 2: max<math>X</math>
|-
| 3: Q1 || || 4: med
|-
| 5: Q2
|}
<!-- Ende Tabelle Menü 6 -->
 
 
Mit <span style="background:yellow">4</span> und <span style="background:yellow">=</span> erhält man den größten Beobachtungswert.
 
Mit <span style="background:yellow">AC</span> beenden.
 
Über <span style="background:yellow">SHIFT</span> und <span style="background:yellow">1</span> neue Größe berechnen.
 
=== Beispiel Beobachtungswerte aus einer Urliste untersuchen ===
{| class="wikitable"
|+ Urliste
! colspan="5"| Gewicht in g
|-
| 150 || 150,5 || 150 || 149,8 || 149,7
|-
| 149,8 || 150 || 150,5 || 149,7 || 150
|}
</div>
 
<!--  Ende Tabelle Gewicht in g -->
Die Firma PurFrucht GmbH produziert auch Früchte-Riegel mit einem Sollgewicht von 150 g. Der laufenden Produktion werden 10 Riegel entnommen und auf ihr Gewicht untersucht.
 
Bestimmen Sie
* den größten Beobachtungswert,
* den kleinsten Beobachtungswert,
* den Median,
* das arithmetische Mittel und
* die Standardabweichung.
 
'''Vorgehen mit dem Taschenrechner:'''
 
Stellen Sie sicher, dass eine Urliste eingegeben werden kann.
<span style="background:yellow">SHIFT</span> <span style="background:yellow">MODE</span>  <span style="background:yellow">↓</span>  <span style="background:yellow">4</span> <span style="background:yellow">2</span>
 
Jetzt geben Sie nacheinander die Werte ein und bestätigen jede einzelne Eingabe mit <span style="background:yellow">=</span>:
 
150 <span style="background:yellow">=</span> 150,5 <span style="background:yellow">=</span> 150 <span style="background:yellow">=</span> 149,8 <span style="background:yellow">=</span> 149,7 <span style="background:yellow">=</span> 149,8 <span style="background:yellow">=</span> 150 <span style="background:yellow">=</span> 150,5 <span style="background:yellow">=</span> 149,7 <span style="background:yellow">=</span> 150 <span style="background:yellow">=</span>
 
Die gesamte Eingabe wird mit <span style="background:yellow">AC</span> beendet.
 
Jetzt wollen Sie im nächsten Schritt Berechnungen durchführen:
<span style="background:yellow">SHIFT</span> <span style="background:yellow">1</span> beginnen jede Berechnung.
* größter Beobachtungswert: <span style="background:yellow">6</span> <span style="background:yellow">2</span> <span style="background:yellow">=</span> liefert 150,5
 
<span style="background:yellow">AC</span> <span style="background:yellow">SHIFT</span> <span style="background:yellow">1</span>


* den kleinsten Beobachtungswert: <span style="background:yellow">6</span> <span style="background:yellow">1</span> <span style="background:yellow">=</span> liefert 149,7


<span style="background:yellow">AC</span> <span style="background:yellow">SHIFT</span> <span style="background:yellow">1</span>


* den Median: <span style="background:yellow">6</span> <span style="background:yellow">4</span> <span style="background:yellow">=</span> liefert 150


Mit 1 und = erhält man den kleinsten Beobachtungswert.
Mit AC beenden. Über SHIFT und 1 neue Größe berechnen.


== Größter Beobachtungswerte x_{Max} ==
<span style="background:yellow">AC</span> <span style="background:yellow">SHIFT</span> <span style="background:yellow">1</span>
Wählt man 6 erhält man:


* das arithmetische Mittel: <span style="background:yellow">4</span> <span style="background:yellow">2</span> <span style="background:yellow">=</span> liefert 150


<span style="background:yellow">AC</span> <span style="background:yellow">SHIFT</span> <span style="background:yellow">1</span>


* die Standardabweichung: <span style="background:yellow">4</span> <span style="background:yellow">3</span> <span style="background:yellow">=</span> liefert 0,2757


Mit 2 und = erhält man den größten Beobachtungswert.
Bei der Eingabe einer Häufigkeitsliste geht es genauso einfach.
Mit AC beenden. Über SHIFT und 1 neue Größe berechnen.


== Median <math>x_{Med}</math> ==
Wählt man 6 erhält man:


== Kurzanleitung ==
Die gibt es hier: [[../Kurzanleitung|Kurzanleitung]]






Mit 4 und = erhält man den größten Beobachtungswert.
{{Beschreibende Statistik}}
Mit AC beenden. Über SHIFT und 1 neue Größe berechnen.

Aktuelle Version vom 15. April 2019, 12:04 Uhr

Zunächst müssen die Daten erfasst werden. Dann kann gerechnet werden.

Datenerfassung

Dabei ist zwischen Beobachtungswerten und Merkmalsausprägungen mit zugehörigen Häufigkeiten zu unterscheiden.

Auswahl zwischen Urliste und Häufigkeitsverteilung

Diese Einstellung nimmt man über ⇧ Shift MODE vor:

1: Mth2D 2: Linear
3: Deg 4: ln X
5: Gra 6: Fix
7: Sci 8: Norm

Dann ↓ wählen und man gelangt zu:

1: ab/c 2: v
3: CMPLX 4: STAT
5: PerD 6: AbAut
7: ←KNTR→

Hier wählt man 4 für STAT und erhält:

Häufigkeit?
1: EIN 2: AUS

Man wählt

  • 1 für die Eingabe absoluter oder relativer Häufigkeitsverteilungen oder
  • 2 für die Eingabe von Beobachtungswerten aus einer Urliste.

Dateneingabe

Über MODE gelangt man ins das folgende Menü:

1: COMP 2: STAT
3: TABLE 4: DIST
5: EQN 6: MATRIX
7: INEQ 8: VECTOR

Man wählt 2 für STAT:

1: 1-VAR 2: A+BX
3: _+cX2 4: ln X
5: e^X 6: A B^X
7: A X^B 8: 1/X

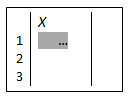
1 für 1-VAR (Häufigkeit für eine Variable) eingeben, liefert:

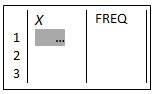
Eingabe einer Urliste Eingabe einer Häufigkeitsverteilung
(Häufigkeit? AUS) (Häufigkeit ? EIN)
Urliste Häufigkeiten

Eingabe einer Urliste

Jetzt werden nacheinander die Beobachtungswerte eingegeben, wobei jeder einzelne Wert mit = zu bestätigen ist.

Das Ende der Eingabe erfolgt über AC.


Eingabe einer Häufigkeitsverteilung

Jetzt werden nacheinander die Merkmalsausprägungen eingegeben, wobei jeder einzelne Wert mit = zu bestätigen ist. Dann ↓ und → zur Spalte FREQ wechseln und hier die zugehörige Häufigkeit (absolut oder relativ) erfassen.

Das Ende der Eingabe erfolgt über AC .

Berechnungen

Über ⇧ Shift und 1 gelangt man in das Statistik-Menü:

1: Type 2: Data
3: Sum 4: Var
5: Distr 6: MinMax

Stichprobenumfang

Wählt man 4 erhält man:

1: 2:
3: 4:

Wählt man 1 und = erhält man bei absoluter Häufigkeitsverteilung den Stichprobenumfang.

Mit AC beenden.

Über ⇧ Shift und 1 neue Größe berechnen.

Artihmetisches Mittel

Wählt man 4 erhält man

1: 2:
3: 4:

Wählt man 2 und = erhält man das arithmetische Mittel.

Mit AC beenden.

Über SHIFT und 1 neue Größe berechnen.

Standardabweichung

Wählt man 4 erhält man

1: 2:
3: 4:

Wählt man 3 und = erhält man die Standardabweichung.

Mit AC beenden.

Über SHIFT und 1 neue Größe berechnen.

Summe der Beobachtungswerte

Wählt man 3 erhält man:

1: 2:

Mit 2 und = erhält man das gewünschte Ergebnis.

Bei Beobachtungswerten erhält man:

Bei einer Häufigkeitsverteilung erhält man:

bzw.

Mit AC beenden.

Über SHIFT und 1 neue Größe berechnen.

Kleinster Beobachtungswerte

Wählt man 6 erhält man:

1: min 2: max
3: Q1 4: med
5: Q2

Mit 1 und = erhält man den kleinsten Beobachtungswert.

Mit AC beenden.

Über SHIFT und 1 neue Größe berechnen.

Größter Beobachtungswerte

Wählt man 6 erhält man:

1: min 2: max
3: Q1 4: med
5: Q2


Mit 2 und = erhält man den größten Beobachtungswert.

Mit AC beenden.

Über SHIFT und 1 neue Größe berechnen.

Median

Wählt man 6 erhält man:

1: min 2: max
3: Q1 4: med
5: Q2


Mit 4 und = erhält man den größten Beobachtungswert.

Mit AC beenden.

Über SHIFT und 1 neue Größe berechnen.

Beispiel Beobachtungswerte aus einer Urliste untersuchen

Urliste
Gewicht in g
150 150,5 150 149,8 149,7
149,8 150 150,5 149,7 150

Die Firma PurFrucht GmbH produziert auch Früchte-Riegel mit einem Sollgewicht von 150 g. Der laufenden Produktion werden 10 Riegel entnommen und auf ihr Gewicht untersucht.

Bestimmen Sie

  • den größten Beobachtungswert,
  • den kleinsten Beobachtungswert,
  • den Median,
  • das arithmetische Mittel und
  • die Standardabweichung.

Vorgehen mit dem Taschenrechner:

Stellen Sie sicher, dass eine Urliste eingegeben werden kann. SHIFT MODE ↓ 4 2

Jetzt geben Sie nacheinander die Werte ein und bestätigen jede einzelne Eingabe mit =:

150 = 150,5 = 150 = 149,8 = 149,7 = 149,8 = 150 = 150,5 = 149,7 = 150 =

Die gesamte Eingabe wird mit AC beendet.

Jetzt wollen Sie im nächsten Schritt Berechnungen durchführen: SHIFT 1 beginnen jede Berechnung.

  • größter Beobachtungswert: 6 2 = liefert 150,5

AC SHIFT 1

  • den kleinsten Beobachtungswert: 6 1 = liefert 149,7

AC SHIFT 1

  • den Median: 6 4 = liefert 150


AC SHIFT 1

  • das arithmetische Mittel: 4 2 = liefert 150

AC SHIFT 1

  • die Standardabweichung: 4 3 = liefert 0,2757

Bei der Eingabe einer Häufigkeitsliste geht es genauso einfach.


Kurzanleitung

Die gibt es hier: Kurzanleitung



Estatística ícone.svg

Lernpfad Beschreibende Statistik

  1. Grundbegriffe
  2. Graphische Darstellungen von Häufigkeitsverteilungen
  3. Lagemaße
    (arithmetisches Mittel, Modus, Median)
  4. Streuungsmaße
    (mittlere absolute Abweichung, mittlere quadratische Abweichung, Standardabweichung)
  5. Einsatz des Taschenrechners
    (Bedienung Casio fx-991DE PLUS)
Abgerufen von „https://unterrichten.zum.de/index.php?title=Beschreibende_Statistik/Einsatz_des_Taschenrechners/ausführliche_Anleitung&oldid=92819“