Beschreibende Statistik/Graphische Darstellung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
main>Matthias Scharwies
Keine Bearbeitungszusammenfassung
(f)
Markierung: 2017-Quelltext-Bearbeitung
 
(2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
Will man mithilfe der Daten einer statistischen Erhebung eine Aussage unterstützen, so bieten sich graphische Darstellungen an. Der Betrachter kann die Daten schnell erfassen und die Aussage bleibt viel leichter im Gedächtnis.
Will man mithilfe der Daten einer statistischen Erhebung eine Aussage unterstützen, so bieten sich '''graphische Darstellungen''' an. Der Betrachter kann die Daten schnell erfassen und die Aussage bleibt viel leichter im Gedächtnis.


Allerdings sind dabei - wie immer - einige wichtige Grundsätze zu beachten. Ansonsten sind auch optisch schöne graphische Darstellungen wenig aussagekräftig.
Allerdings sind dabei - wie immer - einige wichtige Grundsätze zu beachten. Ansonsten sind auch optisch schöne graphische Darstellungen wenig aussagekräftig.
Der erste Abschnitt befasst sich mit Grundlagen zur Erstellung von Diagrammen.


* [[#Grundlegendes zu Diagrammen|Grundlegendes zu Diagrammen]]  
* [[#Grundlegendes zu Diagrammen|Grundlegendes zu Diagrammen]]  
* [[Beschreibende Statistik/Graphische Darstellung/Säulendiagramm|Säulendiagramm]]  
* [[Beschreibende Statistik/Graphische Darstellung/Säulendiagramm|Säulendiagramm]]  
** [[/Übungen Säulendiagramm|Übungen Säulendiagramm]]
* [[Beschreibende Statistik/Graphische Darstellung/Balkendiagramm|Balkendiagramm]]  
* [[Beschreibende Statistik/Graphische Darstellung/Balkendiagramm|Balkendiagramm]]  
** [[/Übungen Balkendiagramm|Übungen Balkendiagramm]]
* [[Beschreibende Statistik/Graphische Darstellung/Kreisdiagramm|Kreisdiagramm]]  
* [[Beschreibende Statistik/Graphische Darstellung/Kreisdiagramm|Kreisdiagramm]]  
* [[Beschreibende Statistik/Graphische Darstellung/Punktwolke |Punktwolke ]]  
* [[Beschreibende Statistik/Graphische Darstellung/Punktwolke |Punktwolke ]]  
|| [[/Übungen Punktwolke |Übungen Punktwolke ]]
 
* [[Beschreibende Statistik/Graphische Darstellung/Auswahl des passenden Diagramms |Auswahl des passenden Diagramms ]]
 


== Grundlegendes zu Diagrammen ==  
== Grundlegendes zu Diagrammen ==  
<u>'''Lernziele:'''</u>
'''Lernziele:'''
* Sie wissen, dass eine gute graphische Darstellung
* Sie wissen, dass eine gute graphische Darstellung
** eine Titel,
** eine Titel,
Zeile 24: Zeile 20:
* Sie erkennen, ob ein Diagramm diesen Regeln genügt.
* Sie erkennen, ob ein Diagramm diesen Regeln genügt.
* Sie können diese Regeln benennen.
* Sie können diese Regeln benennen.
}}
 


Mit Diagrammen lassen sich Häufigkeiten in verschiedener Art und Weise veranschaulichen. Jede nach Art des Merkmals und den zugehörigen Merkmalsausprägungen eignen sich manche Darstellungsformen besonders gut - oder eben nicht wirklich gut.
Mit Diagrammen lassen sich Häufigkeiten in verschiedener Art und Weise veranschaulichen. Jede nach Art des Merkmals und den zugehörigen Merkmalsausprägungen eignen sich manche Darstellungsformen besonders gut - oder eben nicht wirklich gut.


<!-- Beispiel -->
=== Beispiel Wohnorte der Oberstufenschüler ===
{|style="color: black; background-color: #FFFFE0;border-left:solid 2px #FFB90F;border-right:solid 2px #FFB90F;border-top:solid 2px #FFB90F;border-bottom:solid 2px #FFB90F;font-size:100%;font-size:100%;"
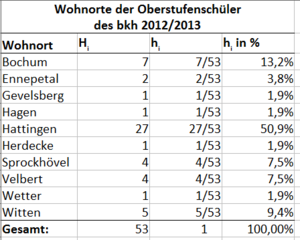
[[Datei:1 Daten.PNG|300px|right|tabellarische Häufigkeitsverteilung]]
! align=left|Beispiel Wohnorte der Oberstufenschüler
|-
|
Liegen die Daten als tabellarische Häufigkeitsverteilung vor, so lassen sich die Informationen zwar gut erkennen, bleiben aber schwer im Gedächtnis.
Liegen die Daten als tabellarische Häufigkeitsverteilung vor, so lassen sich die Informationen zwar gut erkennen, bleiben aber schwer im Gedächtnis.
|-
! align=left|Tabellarische Darstellung
|-
|
[[Datei:1 Daten.PNG|300px|tabellarische Häufigkeitsverteilung]]


Für den Leser sollte man die Daten als Diagramm aufbereiten. Dies gelingt nicht immer:
Für den Leser sollte man die Daten als Diagramm aufbereiten. Dies gelingt nicht immer:
|-
 
! align=left|Schlechte graphische Darstellung
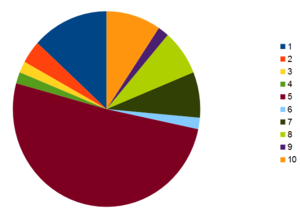
[[Datei:2 schlechte Darstellung.PNG|300px|left|Diagramm ohne Aussagekraft]]
|-
|
[[Datei:2 schlechte Darstellung.PNG|300px|Diagramm ohne Aussagekraft]]


Leider hat wurden hier Titel und Legende vergessen, so dass man als unbedarfter Betrachter gar nicht weiß, was hier dargestellt werden soll. Bleibt auch die Frage, ob ein Kreisdiagramm mit so vielen Segmenten der passende Diagrammtyp ist.
Leider hat wurden hier Titel und Legende vergessen, so dass man als unbedarfter Betrachter gar nicht weiß, was hier dargestellt werden soll. Bleibt auch die Frage, ob ein Kreisdiagramm mit so vielen Segmenten der passende Diagrammtyp ist.


Das geht wirklich besser.
Das geht wirklich besser.
|-
 
! Aussagekräftige graphische Darstellung
'''Aussagekräftige graphische Darstellung'''
|-
|
[[Datei:3 gutes Diagramm.PNG|400px|Gutes Diagramm]]
[[Datei:3 gutes Diagramm.PNG|400px|Gutes Diagramm]]


Hier kann der Betrachter den Inhalt und die Aussage sofort erfassen. Alle Beschriftungen sind vorhanden und aussagekräftig.
Hier kann der Betrachter den Inhalt und die Aussage sofort erfassen. Alle Beschriftungen sind vorhanden und aussagekräftig.


|}
 
<!-- Ende Beispiel -->
<!-- Ende Beispiel -->


Zeile 79: Zeile 62:
Aber wie bereitet man die einzelnen Merkmale besonders aussagekräftig auf?
Aber wie bereitet man die einzelnen Merkmale besonders aussagekräftig auf?


{{Navigation/Lernpfad|
{{Aufgabe|
Sie haben in Ihrem Regelheft ein neues Kapitel '''Graphische Darstellungen''' begonnen und mit dem ersten Merksatz gefüllt.}}
 
== Auswahl des passenden Diagramms ==
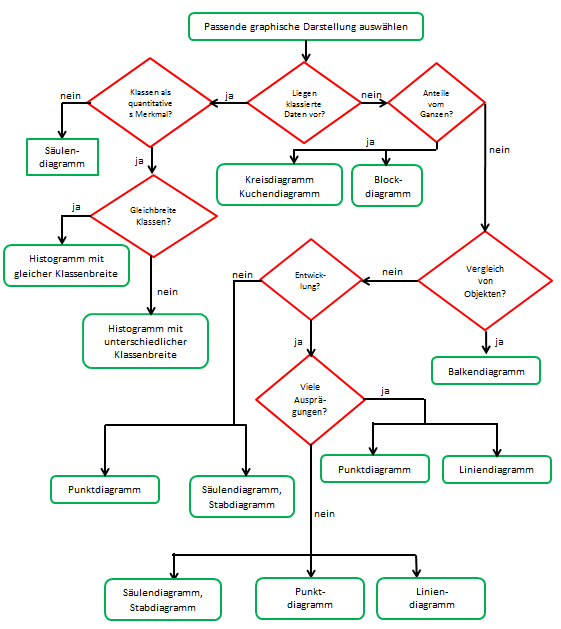
Nicht jeder Diagrammtyp ist gleichermaßen für alle Daten geeignet. Eine Hilfe zur Auswahl des geeigneten Diagrammtyps soll dieses Flussdiagramm liefern:


Sie haben in Ihrem Regelheft ein neues Kapitel '''Graphische Darstellungen''' begonnen und mit dem ersten Merksatz gefüllt.
[[Datei:2 Auswahl Diagramm.PNG|850px|Geeignetes Diagramm wählen]]


== Übungen ==
== Übungen ==
Zeile 88: Zeile 75:


<iframe src="//LearningApps.org/watch?v=pdd5rzbh101" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
<iframe src="//LearningApps.org/watch?v=pdd5rzbh101" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
}}
 


{{Aufgabe|
{{Aufgabe|
Zeile 108: Zeile 95:


{{Fortsetzung|weiter=Säulendiagramm|weiterlink=Beschreibende_Statistik/Graphische_Darstellung/Säulendiagramm}}
{{Fortsetzung|weiter=Säulendiagramm|weiterlink=Beschreibende_Statistik/Graphische_Darstellung/Säulendiagramm}}


{{Beschreibende Statistik}}
{{Beschreibende Statistik}}

Aktuelle Version vom 15. April 2019, 11:13 Uhr

Will man mithilfe der Daten einer statistischen Erhebung eine Aussage unterstützen, so bieten sich graphische Darstellungen an. Der Betrachter kann die Daten schnell erfassen und die Aussage bleibt viel leichter im Gedächtnis.

Allerdings sind dabei - wie immer - einige wichtige Grundsätze zu beachten. Ansonsten sind auch optisch schöne graphische Darstellungen wenig aussagekräftig.


Grundlegendes zu Diagrammen

Lernziele:

  • Sie wissen, dass eine gute graphische Darstellung
    • eine Titel,
    • eine Legende,
    • beschriftete und
    • skalierte Achsen hat.
  • Sie erkennen, ob ein Diagramm diesen Regeln genügt.
  • Sie können diese Regeln benennen.


Mit Diagrammen lassen sich Häufigkeiten in verschiedener Art und Weise veranschaulichen. Jede nach Art des Merkmals und den zugehörigen Merkmalsausprägungen eignen sich manche Darstellungsformen besonders gut - oder eben nicht wirklich gut.

Beispiel Wohnorte der Oberstufenschüler

tabellarische Häufigkeitsverteilung

Liegen die Daten als tabellarische Häufigkeitsverteilung vor, so lassen sich die Informationen zwar gut erkennen, bleiben aber schwer im Gedächtnis.

Für den Leser sollte man die Daten als Diagramm aufbereiten. Dies gelingt nicht immer:

Diagramm ohne Aussagekraft

Leider hat wurden hier Titel und Legende vergessen, so dass man als unbedarfter Betrachter gar nicht weiß, was hier dargestellt werden soll. Bleibt auch die Frage, ob ein Kreisdiagramm mit so vielen Segmenten der passende Diagrammtyp ist.

Das geht wirklich besser.

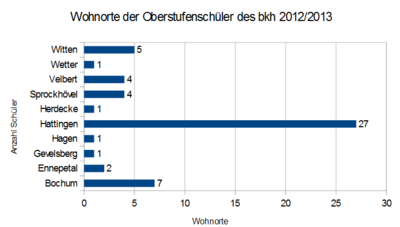
Aussagekräftige graphische Darstellung Gutes Diagramm

Hier kann der Betrachter den Inhalt und die Aussage sofort erfassen. Alle Beschriftungen sind vorhanden und aussagekräftig.


Um die Aussagekraft und Leserlichkeit einer Graphik zu gewährleisten sind einige grundlegende Regeln zu beachten.

Merke

Gute Graphiken haben

  • eine sprechende Überschrift (Titel),
  • beschriftete und
  • skalierte Achsen,
  • beschriftete Segmente oder eine Legende.

Wenn nötig, werden Werte zu den einzelnen Segmenten (Merkmalsausprägungen) angegeben.


Kommen wir zurück zur Eisdiele „Rabe“. Die absoluten und relativen Häufigkeiten der einzelnen Merkmale haben wir schon bestimmt. Diese wollen wir nun graphisch veranschaulichen, um dem Inhaber die wichtigsten Informationen möglichst gut zugänglich zu machen.

Aber wie bereitet man die einzelnen Merkmale besonders aussagekräftig auf?

Aufgabe
Sie haben in Ihrem Regelheft ein neues Kapitel Graphische Darstellungen begonnen und mit dem ersten Merksatz gefüllt.

Auswahl des passenden Diagramms

Nicht jeder Diagrammtyp ist gleichermaßen für alle Daten geeignet. Eine Hilfe zur Auswahl des geeigneten Diagrammtyps soll dieses Flussdiagramm liefern:

Geeignetes Diagramm wählen

Übungen

Aufgabe
Ordnen Sie die richtigen Begriffe zu.


Aufgabe

Was ist bei der graphischen Aufbereitung immer zu beachten?

Gute Graphiken haben

  • eine sprechende Überschrift (Titel),
  • beschriftete und
  • skalierte Achsen,
  • beschriftete Segmente oder eine Legende.

Wenn nötig, werden Werte zu den einzelnen Segmenten (Merkmalsausprägungen) angegeben.



Säulendiagramm


Estatística ícone.svg

Lernpfad Beschreibende Statistik

  1. Grundbegriffe
  2. Graphische Darstellungen von Häufigkeitsverteilungen
  3. Lagemaße
    (arithmetisches Mittel, Modus, Median)
  4. Streuungsmaße
    (mittlere absolute Abweichung, mittlere quadratische Abweichung, Standardabweichung)
  5. Einsatz des Taschenrechners
    (Bedienung Casio fx-991DE PLUS)
Abgerufen von „https://unterrichten.zum.de/index.php?title=Beschreibende_Statistik/Graphische_Darstellung&oldid=92813“