Quadratische Funktionen erkunden/Die Parameter der Scheitelpunktform

Quadratische Funktionen erkunden

• Wiederholung
• Quadratische Funktionen im Alltag
• Quadratische Funktionen kennenlernen
• Die Parameter der Scheitelpunktform
• Die Scheitelpunktform
• Die Parameter der Normalform
• Die Normalform
• Von der Scheitelpunkt- zur Normalform
• Übungen

< Mathematik-digital

In diesem Kapitel lernst du ganz unterschiedlich aussehende Parabeln kennen. Du wirst

1. herausfinden, wie man Parabeln strecken, stauchen und spiegeln kann,
2. entdecken, welche Parameter es in der Scheitelpunktform quadratischer Funktionen gibt.

Mit diesem Wissen kannst du dann selbst verschiedene Parabeln darstellen und beschreiben.

Quadratische Funktionen verändern

Wenn du dir die Bilder von der Seite Quadratische Funktionen im Alltag noch einmal anschaust, dann fällt auf, dass die abgebildeten Parabeln anders aussehen als die gerade kennengelernte Normalparabel. In der Natur und in Anwendungen wird der Funktionsterm der Normalparabel (y = x²) variiert und es entstehen die unterschiedlichsten Parabeln.

• 
• 
• 
• 

Eine Anwendung wird dir im folgenden Video gezeigt. Das Deutsche Zentrum für Luft- und Raumfahrt (DLR) führt seit einigen Jahren Parabelflüge durch.

Vorlage:Video Video: Parabelflug des DLR

Durch unterschiedliche Parabelflüge wird die Schwerkraft, die auf dem Mond bzw. auf dem Mars herrscht, nachempfunden. In der Vorlage:Pdf-extern des DLR kannst du dir die zu fliegenden Parabeln auf Seite 16 (31) angucken.

Strecken, Stauchen und Spiegeln

Achtung

Dieser Abschnitt ist identisch zu dem 1. Abschnitt in dem Kapitel die Parameter der Normalform. Wenn du ihn dort schon bearbeitet hast, kannst du direkt weitergehen zum nächsten Abschnitt "Verschiebung in x-Richtung".

Aufgabe 1

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 4) .

Was passiert, wenn man statt der Funktion $y=x^2$ folgende Funktionen gegeben hat:

(1) $y=2x^2$,          (2) $y=\frac{1}{2}x^2$     und     (3) $y=-x^2$ ?

a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen (ohne diese zu zeichnen!).

Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die drei Funktionen aufstellen und die Funktionswerte mit den Werten von $y=x^2$ vergleichen.

b) Überprüfe deine Vermutungen aus Aufgabenteil a) mit dem folgenden Geogebra-Applet. Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?

In dem Applet ist die Normalparabel $f(x)=x^2$ grau eingezeichnet, die du auf der Seite Quadratische Funktionen kennenlernen erkundet hast. Du kannst verschiedene Werte für "$a=$" eingeben. Dadurch wird der grüne Graph $g(x)=a \cdot x^2$ verändert.

Richtige Vermutungen können wie folgt lauten:

1. Die Parabel von Funktion (1) ist im Vergleich zu der Normalparabel schmaler, da die quadrierten x-Werte ($x^2$) durch den Vorfaktor 2 immer verdoppelt werden. Der zugehörige y-Wert wird dadurch größer.

2. Die Parabel von Funktion (2) ist im Vergleich zu der Normalparabel breiter, da die quadrierten x-Werte ($x^2$) durch den Vorfaktor 1/2 immer halbiert werden. Der zugehörige y-Wert wird dadurch kleiner.

3. Die Parabel von Funktion (3) ist im Vergleich zu der Normalparabel "umgedreht", da die quadrierten x-Werte ($x^2$) durch den Vorfaktor -1 immer negative Werte annehmen. Der y-Wert ist also immer negativ.

Aufgabe 2

In dem folgenden Lückentext werden die Erkenntnisse, die du aus Aufgabe 1 mitnehmen konntest, noch einmal ausformuliert. Füge die fehlenden Begriffe und Zahlen in die Lücken.

Schau nochmal in deine Lösung zu Aufgabe 1. Du kannst auch erneut verschiedene Werte für a in dem Applet dort eingeben und die Auswirkungen auf den Graphen betrachten.

Wenn a kleiner Null ist ($a<0$), dann ist die Parabel nach unten geöffnet.

Wenn a größer Null ist ($a>0$), dann ist die Parabel nach oben geöffnet.

Wenn a zwischen minus Eins und Eins liegt ($-1<a<1$), dann wird der Graph der Funktion breiter. Man nennt das auch eine gestauchte Parabel.

Wenn a kleiner als minus Eins ($a<-1$) oder größer als Eins ist ($a>1$), dann wird der Graph der Funktion gestreckt. Er ist somit schmaler als die Normalparabel.

Aufgabe 3

Knobelaufgabe

Tipp: Wenn du die Kärtchen mit den Graphen anklickst, werden sie dir vergrößert angezeigt.

Aufgabe 4

Für diese Aufgabe benötigst du deinen Hefter (Merksätze, S. 2) .

Lies dir den folgenden Merksatz aufmerksam durch. Ergänze ihn durch beispielhafte Funktionsterme.

Merke

Multipliziert man $y=x^2$ mit einem Faktor a, wird die Parabel gestreckt, gestaucht und/oder gespiegelt. $y=ax^2$ (mit a≠0) ergibt demnach für:

a > 0: Die Parabel ist nach oben geöffnet.

a < 0: Die Parabel ist nach unten geöffnet.

a < -1 bzw. a > 1: Die Parabel ist gestreckt.

-1 < a < 1: Die Parabel ist gestaucht.

Der Parameter a wird auch Streckungsfaktor genannt.

Verschiebung in x-Richtung

Aufgabe 5

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 5) .

Was passiert, wenn man statt der Funktion $y=x^2$ folgende Funktionen gegeben hat:

(1) $y=(x-2)^2$          (2) $y=(x+2)^2$ ?

a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!).

Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die zwei Funktionen aufstellen und die Funktionswerte mit den Werten von $y=x^2$ vergleichen.

b) Überprüfe deine Vermutungen aus Aufgabenteil a) mit dem folgenden Geogebra-Applet. Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?

In dem Applet ist die Normalparabel $f(x)=x^2$ grau eingezeichnet, die du auf der Seite Quadratische Funktionen kennenlernen erkundet hast. Du kannst verschiedene Werte für "$d=$" eingeben. Dadurch wird der grüne Graph $g(x)=(x-d)^2$ verändert.

Richtige Vermutungen können wie folgt lauten:

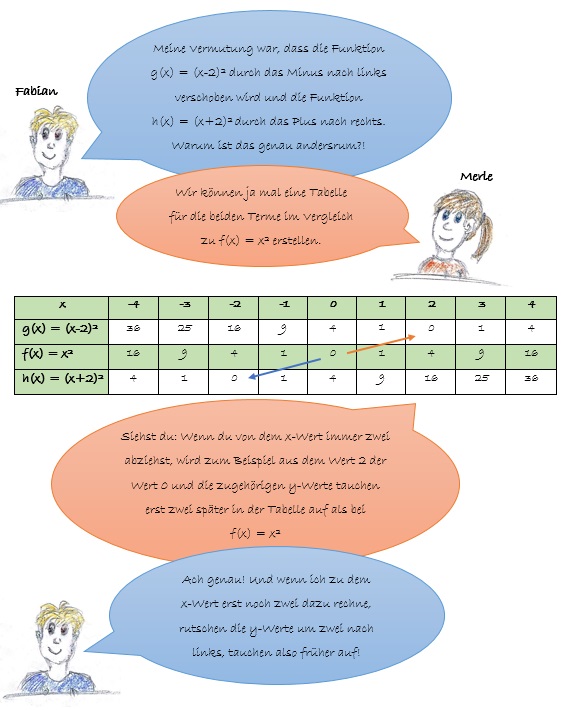
1. Die Parabel von Funktion (1) ist im Vergleich zu der Normalparabel nach rechts verschoben, da die x-Werte vor dem quadrieren mit 2 subtrahiert werden ($(x-2)^2$). Der Scheitelpunkt liegt nicht mehr bei $S_1(0|0)$, sondern weiter rechts im Punkt $S_2(2|0)$.

2. Die Parabel von Funktion (2) ist im Vergleich zu der Normalparabel nach links verschoben, da die x-Werte vor dem quadrieren mit 2 addiert werden ($(x+2)^2$). Der Scheitelpunkt liegt nicht mehr bei $S_1(0|0)$, sondern weiter links im Punkt $S_2(-2|0)$.

Aufgabe 6

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 6) .

Fabians Vermutung darüber, wie sich der Graph einer Funktion verändert, wenn man zu dem x‑Wert etwas addiert oder subtrahiert steht im Widerspruch zu seinen Beobachtungen in dem Applet. Merle versucht diesen vermeintlichen Widerspruch mit Hilfe einer Tabelle zu erklären.

a) Lies dir die Unterhaltung von Fabian und Merle durch und versuche die Begründung nachzuvollziehen.

b) Erstelle geschickt ohne zu rechnen eine Tabelle für die Funktion $y=(x+3)^2$.

1. Zeichne eine Tabelle wie sie in Aufgabenteil a) dargestellt ist in deinen Hefter.

2. Füge zunächst nur die x-Werte hinzu, für die du die Tabelle erstellen möchtest - zum Beispiel von -6 bis 2.

3. Wie ist der Term $y=(x+3)^2$ im Vergleich zu $y=x^2$ verschoben? Schau dir an, mit welchem Trick Merle und Fabian die Tabelle in Aufgabenteil a) erstellt haben.

Die Tabelle für $y=(x+3)^2$ sieht wie folgt aus:

Aufgabe 7

Für diese Aufgabe benötigst du deinen Hefter (Merksätze, S. 2) .

Lies dir den folgenden Merksatz aufmerksam durch. Ergänze ihn durch beispielhafte Funktionsterme.

Merke

Addiert oder subtrahiert man eine Zahl d von x vor dem Quadrieren, so wird die Parabel entlang der x-Achse verschoben. Für $y=(x-d)^2$ gilt:

d > 0: Die Parabel wird entlang der x-Achse nach rechts verschoben.

d < 0: Die Parabel wird entlang der x-Achse nach links verschoben.

Verschiebung in y-Richtung

Aufgabe 8

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 6) .

Was passiert, wenn man statt der Funktion $y=x^2$ folgende Funktionen gegeben hat:

(1) $y=x^2+3$          (2) $y=x^2-3$ ?

a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!).

Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die beiden Funktionen aufstellen und die Funktionswerte mit den Werten von $y=x^2$ vergleichen.

b) Überprüfe deine Vermutungen aus Aufgabenteil a) mit dem folgenden Geogebra-Applet. Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?

In dem Applet ist die Normalparabel $f(x)=x^2$ grau eingezeichnet, die du auf der Seite Quadratische Funktionen kennenlernen erkundet hast. Du kannst verschiedene Werte für "$e=$" eingeben. Dadurch wird der grüne Graph $g(x)=x^2+e$ verändert.

Richtige Vermutungen können wie folgt lauten:

1. Die Parabel von Funktion (1) ist im Vergleich zu der Normalparabel nach oben verschoben, da die x-Werte nach dem quadrieren mit 3 addiert werden.

2. Die Parabel von Funktion (2) ist im Vergleich zu der Normalparabel nach unten verschoben, da die x-Werte nach dem quadrieren mit 3 subtrahiert werden.

Aufgabe 9

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 7-8) .

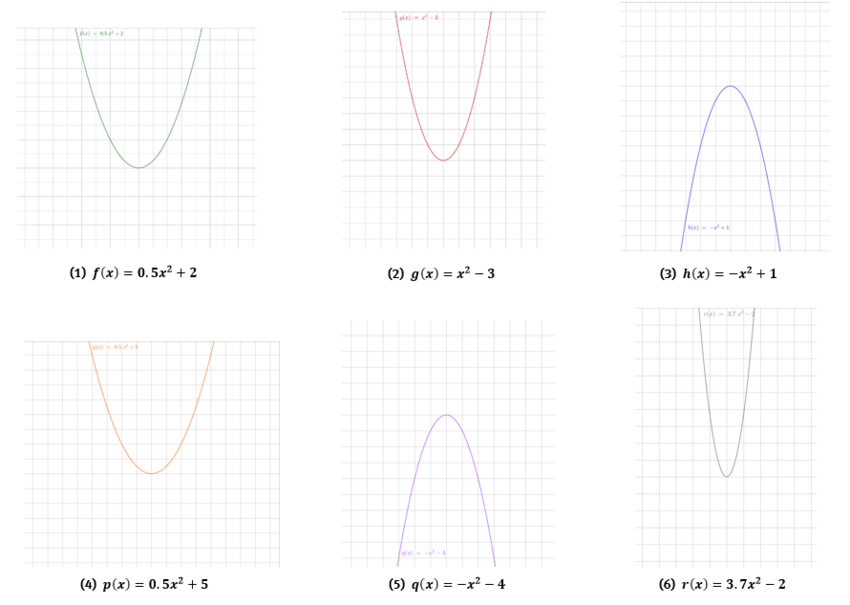
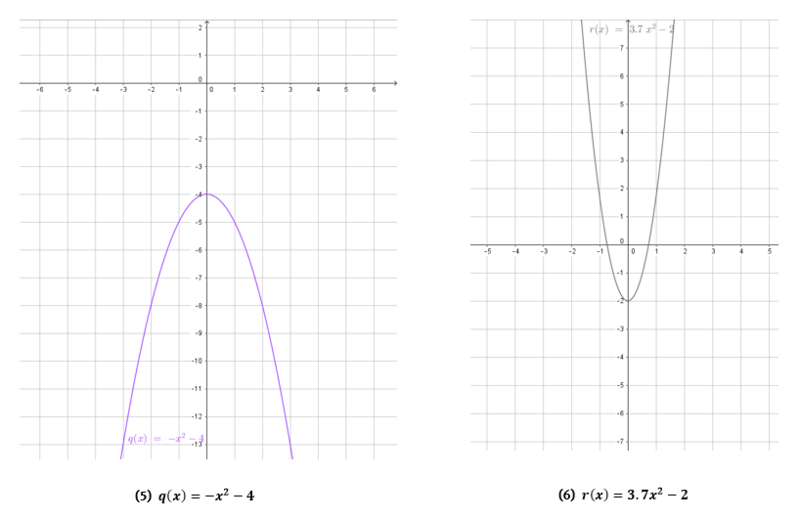
Graphen zeichnen einmal „verkehrt herum”: Bei dieser Aufgabe sind die Funktionsgraphen und Terme bereits gezeichnet bzw. angegeben. Was fehlt, sind die passenden Koordinatensysteme.

a) Zeichne in deinem Hefter die passenden Koordinatensysteme für drei der quadratischen Funktionen:

Der Parameter d kommt bei keiner der Parabeln vor, das heißt der Graph ist weder nach rechts noch nach links verschoben.

Der Parameter a sorgt für eine Stauchung oder Streckung der Parabel. Der Parameter e verschiebt die Parabel in y-Richtung, also entlang der y-Achse nach oben oder unten.

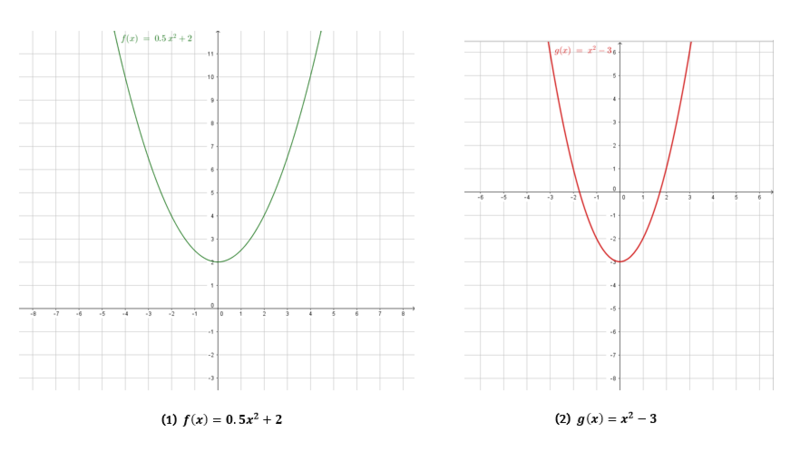
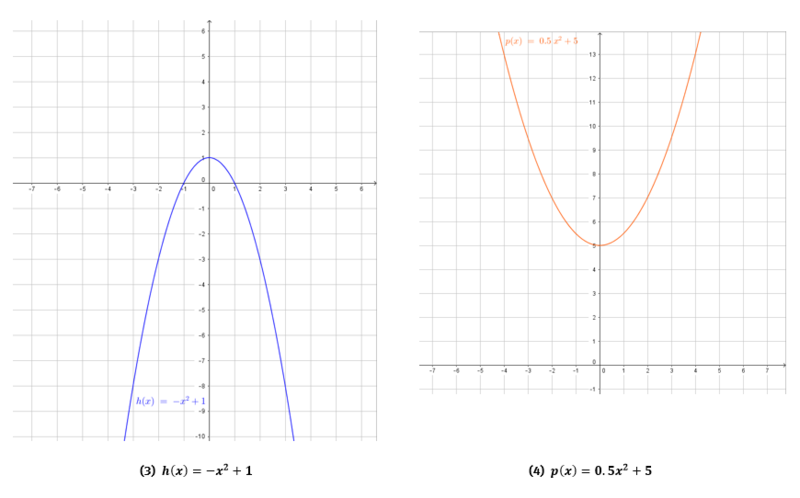
Nutze für die Abstände auf der x- und y-Achse jeweils 1 Kästchen und gehe in Einserschritten voran.

Die Koordinatensysteme zu den Parabeln und Funktionstermen sollten wie folgt liegen:

Für die Lage der Achsen ist wichtig, dass für alle Funktionen hier gilt: $d=0$.

Daraus folgt, dass der Scheitelpunkt jeder Parabel hier auf der y-Achse liegt. Seine Koordinaten sind also jeweils $S(0|e)$.

Die x-Achse liegt e Einheiten von dem Scheitelpunkt entfernt. Je nach Vorzeichen von e über oder unter dem Scheitelpunkt.

Der Maßstab der Achsen muss so gewählt sein, dass jedes Kästchen für eine Einheit steht. Sonst passen die Werte der anderen Punkte der Parabeln nicht zu der Funktionsgleichung.

b) Wenn du das Koordinatensystem für die Funktion $(1) y=0,5\cdot x^2+2$ gezeichnet hast, wie kommst du dann ganz einfach auf das Koordinatensystem der Funktion $(4) y=0,5\cdot x^2+5$? Formuliere einen Tipp.

Ein Tipp könnte wie folgt lauten:

Aufgabe 10

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 8) .

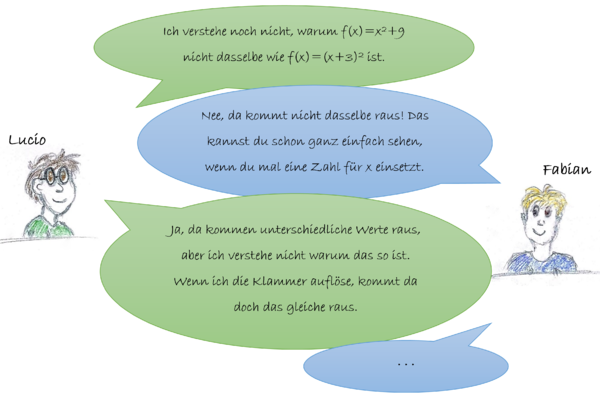
Lucio hat noch ein Problem bei der Unterscheidung von Termen in der Form $f(x)=x^2+9$ und $f(x)=(x+3)^2$. Lies dir die folgende Unterhaltung durch. Führe sie anschließend in deinem Hefter fort, indem du dir eine Antwort auf Lucios Problem überlegst.

Schaue dir noch einmal die Binomischen Formeln an.

Die Terme $f(x)=(x+3)^2$ und $f(x)=x^2+9$ sind nicht gleich.

Man darf das Quadrat nicht einfach in die Klammer von $f(x)=(x+3)^2$ ziehen: $f(x)=(x+3)^2\neq x^2+3^2$

Die erste Binomische Formel besagt vielmehr:

$f(x)=(x+3)^2=(x+3)(x+3)=x^2+3x+3x+9=x^2+6x+9$.

Aufgabe 11

Für diese Aufgabe benötigst du deinen Hefter (Merksätze, S. 3) .

Lies dir den folgenden Merksatz aufmerksam durch. Ergänze ihn durch beispielhafte Funktionsterme.

Merke

Addiert oder subtrahiert man eine Zahl e von $y=x^2$, wird die Parabel entlang der y-Achse verschoben. Für $y=x^2+e$ gilt:

e > 0: Die Parabel wird entlang der y-Achse nach oben verschoben.

e < 0: Die Parabel wird entlang der y-Achse nach unten verschoben.

Zusammenfassung der wichtigsten Inhalte

Hier sind die Merksätze, die dir auf dieser Seite begegnet sind, noch einmal gesammelt dargestellt.

Merke

Multipliziert man $y=x^2$ mit einem Faktor a, wird die Parabel gestreckt, gestaucht und/oder gespiegelt. $y=ax^2$ (mit a≠0) ergibt demnach für:

a > 0: Die Parabel ist nach oben geöffnet.

a < 0: Die Parabel ist nach unten geöffnet.

a < -1 bzw. a > 1: Die Parabel ist gestreckt.

-1 < a < 1: Die Parabel ist gestaucht.

Der Parameter a wird auch Streckungsfaktor genannt.

Merke

Addiert oder subtrahiert man eine Zahl d von x vor dem Quadrieren, so wird die Parabel entlang der x-Achse verschoben. Für $y=(x-d)^2$ gilt:

d > 0: Die Parabel wird entlang der x-Achse nach rechts verschoben.

d < 0: Die Parabel wird entlang der x-Achse nach links verschoben.

Merke

Addiert oder subtrahiert man eine Zahl e von $y=x^2$, wird die Parabel entlang der y-Achse verschoben. Für $y=x^2+e$ gilt:

e > 0: Die Parabel wird entlang der y-Achse nach oben verschoben.

e < 0: Die Parabel wird entlang der y-Achse nach unten verschoben.

Die auf dieser Seite gewonnen Erkenntnisse können kombiniert werden und ergeben quadratische Funktion der Form $y=a(x-d)^2+e$. Diese Form heißt Scheitelpunktform, da die Parameter d und e die Koordinaten des Scheitelpunktes $S(d|e)$ der Parabel angeben.

Auf der nächsten Seite lernst du diese Variante quadratischer Funktionen genauer kennen. Außerdem befinden sich noch weitere Übungsaufgaben in dem Kapitel Übungen.

Die Scheitelpunktform

Erstellt von: Elena Jedtke (Diskussion)