Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Quadratische Funktionen erkunden/Von der Scheitelpunkt- zur Normalform: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Elena Jedtke (Merksatz dazu) |
Main>Elena Jedtke KKeine Bearbeitungszusammenfassung |
||
| Zeile 213: | Zeile 213: | ||
<iframe scrolling="no" title="SPF und NF im Vergleich" src="https://www.geogebra.org/material/iframe/id/R9CvVq59/width/800/height/570/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="800px" height="570px" style="border:0px;"> </iframe> | <iframe scrolling="no" title="SPF und NF im Vergleich" src="https://www.geogebra.org/material/iframe/id/R9CvVq59/width/800/height/570/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="800px" height="570px" style="border:0px;"> </iframe> | ||
{{Aufgaben|2|'''Für diese Aufgabe benötigst du deinen Hefter''' [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
Notiere die folgenden Merksätze in deine Merkliste und ergänze sie durch ein Beispiel.}} | |||
| Zeile 222: | Zeile 228: | ||
Eine Parabel kann immer in beiden Darstellungsformen beschrieben werden.}} | Eine Parabel kann immer in beiden Darstellungsformen beschrieben werden.}} | ||
{{Merke|Durch Ausmultiplikation des Terms einer quadratischen Funktion in Scheitelpunktform, erhält man den zugehörigen Term in Normalform.}} | {{Merke|Durch Ausmultiplikation des Terms einer quadratischen Funktion in Scheitelpunktform, erhält man den zugehörigen Term in Normalform.}} | ||
{{Aufgaben| | |||
{{Aufgaben|3|<!--Unterhaltung zwischen Merle, Fabian und Lucio einfügen, darüber dass die Parameter c und e nicht identisch sind.-->}} | |||
Version vom 21. Juli 2017, 13:09 Uhr
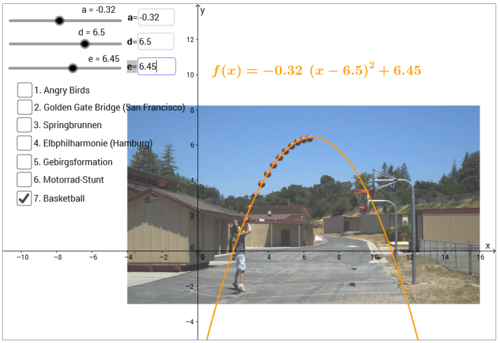
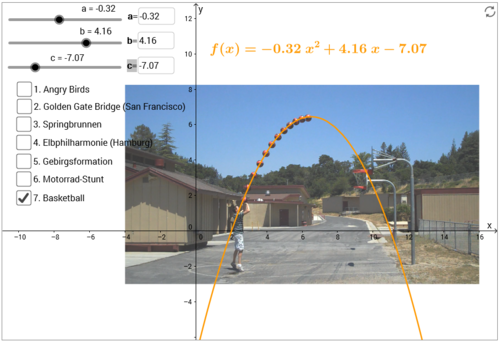
| In diesem Kapitel kannst du herausfinden, wie du quadratischen Funktionen in Scheitelpunktform in quadratische Funktionen in Normalform umwandeln kannst. |
Aufgabe 1
Das folgende Applet kannst du nutzen, um deine Ergebnisse aus Aufgabe 1 zu kontrollieren. Außerdem kannst du mit den Parametern beider Darstellungsformen experimentieren und zum Beispiel untersuchen, wie du die Parameterwerte verändern musst, um beide Graphen an einer beliebigen Stelle im Koordinatensystem übereinander zu legen.
Aufgabe 2
Merke
Parabeln können auf verschiedene Weisen in Termen dargestellt werden. Die beiden Formen, die du bisher kennengelernt hast, heißen
Eine Parabel kann immer in beiden Darstellungsformen beschrieben werden.
Merke
Durch Ausmultiplikation des Terms einer quadratischen Funktion in Scheitelpunktform, erhält man den zugehörigen Term in Normalform.
Aufgabe 3
Erstellt von: Elena Jedtke (Diskussion)