GeoGebra: Unterschied zwischen den Versionen
(→GeoGebra im Mathematik-Unterricht: -> GeoGebra im Unterricht) |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (25 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
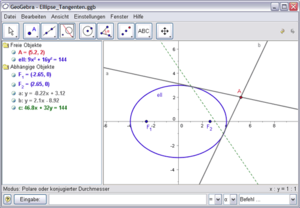
[[Bild:geogebra_geo.png||thumb|Beispiel Ellipsen und Tangenten]] | [[Bild:geogebra_geo.png||thumb|Beispiel Ellipsen und Tangenten]] | ||
'''GeoGebra''' ist eine dynamische | '''GeoGebra''' ist eine dynamische Mathematik-Software, die [[:Kategorie:Geometrie|Geometrie]], [[Algebra]] und [[Analysis]] verbindet. Sie wurde für den Unterricht in den Sekundarstufen von Markus Hohenwarter ursprünglich an der Universität Salzburg entwickelt.<ref>[http://www.geogebra.at Eigendarstellung auf www.geogebra.at]</ref>. Inzwischen ist GeoGebra ein internationales Projekt, das Unterstützung aus verschiedenen Ländern enthält. | ||
== | '''Geogebra''' | ||
*ist kostenlos und plattformunabhängig (siehe [[Java]]); | |||
*muss nicht installiert werden, die aktuellste Version ist immer über den [http://www.geogebra.org/cms/index.php?option=com_content&task=blogcategory&id=70&Itemid=57 Webstart] verfügbar; | |||
*bietet die Möglichkeit, fertige Arbeitsflächen in eigene Internet-Seiten zu integrieren, sodass Arbeitsblätter im Internet-Browser bearbeitet werden können; | |||
*bietet starke [[Algebra]]-Fähigkeiten; | |||
*ist auch als Funktionsplotter einsetzbar. | |||
*kann Grafiken komplett nach LaTeX exportieren. | |||
==Angebote auf der Homepage www.GeoGebra.org== | |||
''' | *Es gibt ein '''[https://wiki.geogebra.org/de/Handbuch GeoGebra-Wiki]''', das als Handbuch fungiert. Aus GeoGebra heraus weist die Hilfe immer auf eine Seite im Wiki, in der jeweiligen Sprache. Benutzer können eigene Beiträge leisten, indem sie Erläuterungen und Beispiele ergänzen. Dazu muss man sich im Wiki anmelden. Es gibt auch einige ergänzende Seite, wie etwa zu LaTeX | ||
*Es gibt ein '''[https://help.geogebra.org/ GeoGebra-Forum]''', in dem man Fragen bei Problemen stellen, Vorschläge für Neuerungen melden und Hinweise auf Fehler geben kann. Im deutschen Bereich gibt es einige erfahrene Anwender, die schnell und kompetent helfen können.''Auch internationale Foren-Bereiche sind vorhanden!'' | |||
* Es gibt ein [ | |||
* Es gibt | *Es gibt die '''Material-Plattform [https://www.geogebra.org/ geogebra.org]''', auf der man sein Material unter einer CC-BY-SA Lizenz veröffentlichen kann. Aufgrund der Lizenz können Sie auch das Material von anderen kopieren und verändern. GeoGebraTube bietet außerdem die Möglichkeit die Zeichnungen in HTML5 auf mobilen Geräten anzeigen zu lassen, Material von anderen zu nutzen und sie zu GeoGebraBooks zu verbinden. Auf GeoGebraTube hochgeladene Zeichnungen (egal ob von Ihnen oder einem anderen Benutzer) können in das ZUM-Wiki eingebunden werden. | ||
==Fähigkeiten von GeoGebra== | ==Fähigkeiten von GeoGebra== | ||
===Neueste Version von GeoGebra=== | ===Neueste Version von GeoGebra=== | ||
Die | Die am 1. Dezember 2013 erschienene Version 4.4 weist ein paar kleine Änderungen auf. Mehr dazu in den [https://wiki.geogebra.org/s/en/index.php?title=Release_Notes_GeoGebra_4.4 Release-Notes]. | ||
===Zukunft von GeoGebra=== | ===Zukunft von GeoGebra=== | ||
Die nächste größere Änderung wird in der Version 5.0 die Einführung einer 3D-Ansicht sein. Eine Beta-Version ist zum Testen [http://www.geogebra.org/forum/viewtopic.php?f=52&t=19846 verfügbar] und hat bereits beachtlich Fähigkeiten. Mehr dazu in den [http://wiki.geogebra.org/en/Release_Notes_GeoGebra_5.0 Release-Notes], die aber noch erweitert werden. | |||
Die Seite [http://wikis.zum.de/geogebra-rlp/GeoGebra3D_-_Anwendung_in_der_Linearen_Algebra GeoGebra3D - Anwendung in der Linearen Algebra] auf dem Wiki der GeoGebra-Instituts Landau (Rheinland-Pfalz) enthält einige Informationen für Anfänger, mit Anleitungsvideos und Übungsaufgaben. | |||
==Einsatzmöglichkeiten== | |||
===… als interaktives Geometrie-Programm:=== | |||
==Einsatzmöglichkeiten == | |||
=== | |||
Hier hat GeoGebra inzwischen die Konkurrenz mehr als eingeholt. Es bietet nicht nur die üblichen Zeichenfunktionen, sondern es können auch selber Werkzeuge definiert werden und Animationen sind mit Hilfe von Schiebereglern möglich. | Hier hat GeoGebra inzwischen die Konkurrenz mehr als eingeholt. Es bietet nicht nur die üblichen Zeichenfunktionen, sondern es können auch selber Werkzeuge definiert werden und Animationen sind mit Hilfe von Schiebereglern möglich. | ||
| Zeile 54: | Zeile 37: | ||
::<tt>H = Wenn[IstDefiniert[H1],H1,H2] </tt> | ::<tt>H = Wenn[IstDefiniert[H1],H1,H2] </tt> | ||
::: ''Wenn H1 definiert ist, dann soll H dem Punkt H1 entsprechen (der unsichtbar sein kann!), ansonsten soll H gleich H2 sein.'' | :::''Wenn H1 definiert ist, dann soll H dem Punkt H1 entsprechen (der unsichtbar sein kann!), ansonsten soll H gleich H2 sein.'' | ||
'''Ist für eine Zeichnung eine unbestimmte oder dynamisch festgelegt Anzahl an Objekten nötig, so kann man den Befehl Folge verwenden.''' | '''Ist für eine Zeichnung eine unbestimmte oder dynamisch festgelegt Anzahl an Objekten nötig, so kann man den Befehl Folge verwenden.''' | ||
| Zeile 65: | Zeile 48: | ||
'''Weitere Besonderheiten:''' | '''Weitere Besonderheiten:''' | ||
=== ... als Funktionsplotter === | *'''Zufallszahlen''' ermöglichen das Erstellen von immer wieder neuen Aufgabenstellungen. | ||
*Mit '''Kontrollästchen''' können Teile der Zeichnung unsichtbar gemacht werden. '''''Tipp:''' Kombiniert man "Wenn" mit Kontrollkästchen, können Ausgangsbedingungen einer Zeichnung über ein Kontrollkästchen festgelegt werden.'' | |||
===... als Funktionsplotter=== | |||
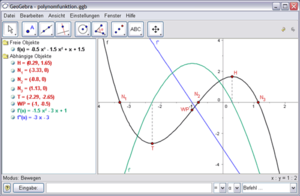
[[Bild:geogebra_kurven.png|thumb|Kurvendiskussion]] | [[Bild:geogebra_kurven.png|thumb|Kurvendiskussion]] | ||
'''Geogebra''' ist als | '''Geogebra''' ist als Funktionenplotter für die Sekundarstufen I und II geeignet: | ||
* Parameter können mit der Maus oder den Pfeiltasten stufenweise verändert werden. | |||
* Der Funktionsterm wird beim Verschieben des Graphen (mit Maus oder Pfeiltasten) automatisch angepasst. | *Parameter können mit der Maus oder den Pfeiltasten stufenweise verändert werden. | ||
* Kurvenscharen können animiert und die "Spuren" angezeigt werden. | *Der Funktionsterm wird beim Verschieben des Graphen (mit Maus oder Pfeiltasten) automatisch angepasst. | ||
* Ableitungen und Flächen unter Graphen können dargestellt und berechnet werden. | *Kurvenscharen können animiert und die "Spuren" angezeigt werden. | ||
*Ableitungen und Flächen unter Graphen können dargestellt und berechnet werden. | |||
Zeichenaufgaben können auf fast natürlich mathematische Weise erledigt werden. Zwingend ist dabei die Nutzung der Funktionsdefinition möglich und bietet, richtig angewandt, die Möglichkeit den Schülern zu verdeutlichen, wie und warum man die Funktionsschreibweise verwendet. | Zeichenaufgaben können auf fast natürlich mathematische Weise erledigt werden. Zwingend ist dabei die Nutzung der Funktionsdefinition möglich und bietet, richtig angewandt, die Möglichkeit den Schülern zu verdeutlichen, wie und warum man die Funktionsschreibweise verwendet. | ||
| Zeile 85: | Zeile 70: | ||
<center> | <center> | ||
<ggb_applet height="650" width="800" | <ggb_applet height="650" width="800" showmenubar="true" showreseticon="true" filename="Graph_Rauchen.ggb" /> | ||
</center> | </center> | ||
| Zeile 91: | Zeile 76: | ||
:<pre><ggb_applet height="650" width="800" showMenuBar="true" showResetIcon="true" filename="Graph_Rauchen.ggb" /></pre> | :<pre><ggb_applet height="650" width="800" showMenuBar="true" showResetIcon="true" filename="Graph_Rauchen.ggb" /></pre> | ||
=== | ===… als Tabellenkalkulation=== | ||
Seit der Version 3.2 bietet GeoGebra eine Tabelle mit den grundlegenden Fähigkeiten einer Tabellenkalkulation wie | Seit der Version 3.2 bietet GeoGebra eine Tabelle mit den grundlegenden Fähigkeiten einer Tabellenkalkulation wie Calc und Excel: | ||
* Autovervollständigung bei Zahlen. | |||
* Man kann Rechenformeln und Text eingeben. | *Autovervollständigung bei Zahlen. | ||
* Formeln kennen absolute und relative Adressierung und können kopiert werden. | *Man kann Rechenformeln und Text eingeben. | ||
* Bereich können markiert und erfasst werden. | *Formeln kennen absolute und relative Adressierung und können kopiert werden. | ||
*Bereich können markiert und erfasst werden. | |||
Speziell in GeoGebra vorhanden sind zusätzlich noch die folgenden Fähigkeiten: | Speziell in GeoGebra vorhanden sind zusätzlich noch die folgenden Fähigkeiten: | ||
* Jede Zelle kann jede Art von Objekt enthalten, also auch Strecken, Integral, Funktion usw. und es sind damit alle üblichen Rechenfunktionen verwendbar. Auch hier wird die Adressierung beachtet. | |||
* Zeichen-Objekte aus der Tabelle werden direkt angezeigt | *Jede Zelle kann jede Art von Objekt enthalten, also auch Strecken, Integral, Funktion usw. und es sind damit alle üblichen Rechenfunktionen verwendbar. Auch hier wird die Adressierung beachtet. | ||
* Aus Zelleninhalten können Listen und Matrizen erstellt werden. | *Zeichen-Objekte aus der Tabelle werden direkt angezeigt | ||
* In Formeln können auch alle Werte aus GeoGebra verwendet werden, wie Schiebregler und Funktionen. | *Aus Zelleninhalten können Listen und Matrizen erstellt werden. | ||
*In Formeln können auch alle Werte aus GeoGebra verwendet werden, wie Schiebregler und Funktionen. | |||
Dank diese Tabelle kann man nun auf dein Einsatz reiner Tabellenkalkulationsprogramme verzichten und hat gleichzeitig noch die Zeichenfähigkeit, wie sie in Tabellenkalkulationsprogrammen nicht vorhanden sind. Auch ein Diagramm-Editor kann da bei weitem nicht mithalten! | Dank diese Tabelle kann man nun auf dein Einsatz reiner Tabellenkalkulationsprogramme verzichten und hat gleichzeitig noch die Zeichenfähigkeit, wie sie in Tabellenkalkulationsprogrammen nicht vorhanden sind. Auch ein Diagramm-Editor kann da bei weitem nicht mithalten! | ||
| Zeile 111: | Zeile 98: | ||
==GeoGebra im Unterricht== | ==GeoGebra im Unterricht== | ||
* [http://www.geogebra.org/de/wiki/index.php/Hauptseite GeoGebra-Wiki] mit Unterrichtsmaterialien und und Arbeitsblättern zum Download. | *[http://www.geogebra.org/de/wiki/index.php/Hauptseite GeoGebra-Wiki] mit Unterrichtsmaterialien und und Arbeitsblättern zum Download. | ||
* [http://www.realmath.de | *[http://www.realmath.de www.realmath.de] - zahlreiche Beispiele, die zeigen, wie GeoGebra im Unterricht eingesetzt werden kann. | ||
* [http://superlehrer.de/index.php?title=GeoGebra Private Sammlung] von Arbeitsblättern, die GeoGebra nutzen. Es wird Wert darauf gelegt, dass es nicht nur Aufgabenblätter sind, die "eine" Antwort erwarten. Es soll geforscht werden. | *[http://superlehrer.de/index.php?title=GeoGebra Private Sammlung] von Arbeitsblättern, die GeoGebra nutzen. Es wird Wert darauf gelegt, dass es nicht nur Aufgabenblätter sind, die "eine" Antwort erwarten. Es soll geforscht werden. | ||
==Video-Hilfen== | ==Video-Hilfen== | ||
==Einsatzgebiete außerhalb der Mathematik== | ==Einsatzgebiete außerhalb der Mathematik== | ||
== GeoGebra-Dateien im ZUM-Wiki == | *[[Informatik]]: [http://www.geogebra.at/de/wiki/index.php/Turtlegrafik Turtlegrafik in Geogebra] - Realisierung einer rudimentären Turtlegrafik mit geogebra auf Grundlage eines Objektes Schildkroete. ([[JavaScript]]) | ||
*[[Wirtschaft]]: [http://www.geogebra.at/de/wiki/index.php/Gleichgewichtspreis Gleichgewichtspreis] - Interaktive Animation | |||
GeoGebra-Dateien (mit der Dateiendung .ggb) können ins [[Hauptseite|ZUM-Wiki]] und in jedes Wiki der | |||
==GeoGebra-Dateien im ZUM-Wiki== | |||
GeoGebra-Dateien (mit der Dateiendung .ggb) können ins [[Hauptseite|ZUM-Wiki]] und in jedes Wiki der Wiki-Family hochgeladen werden. | |||
*[http://wikihilfe.zum.de/wiki/GeoGebra Wiki-Hilfe: GeoGebra] | |||
Hochgeladene ggb-Dateien können dann entweder | Hochgeladene ggb-Dateien können dann entweder intern verlinkt werden oder direkt angezeigt werden, wie die folgenden Beispiele zeigen: | ||
<ggb_applet width="500" height="400" | <ggb_applet width="500" height="400" version="3.2" ggbbase64="UEsDBBQACAAIANyplzsAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjdc6M2EH/u/RUa3oMRIDAzdm6cZKaTmbTXaa730DcBsq0GEEUisf3X30oCjJ2Pu2Tc6eXyQrRar3Z/v/0QzD5uygLds0ZyUc0d7HoOYlUmcl6t5k6rlmdT5+P5h9mKiRVLG4qWoimpmjuB6zta3vLzD7/M5Fo8IFoYlS+cPcydJS0kc5CsG0ZzuWZMHchpu+EFp832U/oPy5Tcb1gj11XdwimqaUGWlfkNl/1yYg6sC66u+D3PWYMKkc2diIDr8N8X1iie0WLuhJ6V+BAXCQ82QRTo3bVo+E5USqvvjS9BgpDkOwa/9LVsNjGBzlibFTzntNLBGD9ACaEHnqu11sVwzJrx1RqcDaPEmsuEaPLbrVSsRJu/WSPmjo+JRnprV4FdSXAMTiSe2RqvjBl2f8uUAl4kohsme3BWDc8H9PTiWl6IYi+qBa/UJa1V2xhOg050q7baPhzVaH8X1apgnQwD5GuW3aVic2tBCKzpz9va/MT4k64uRSEa1EA4hIBC90zt0+hoRwctz+h4RqOzoY0O+zjxjYZ5pvZptApeWde6wHEfNfb6Y7hEWqBRhFTssSloyoBZB7UVVzf9AjLgbh+p1v+9LVMogXEODCbxiUzOJkfJM7tjTcUKmyEVENuKVqJ7nYqWOuNHzjJewtJudIBQTdZf4ICV5mzVsN5vWz8WLrPrjbPwSDyb9E5oHyT4miloBBCP0rHoOlVQI3Pn1z8/OSinSgt1HRSsZFAkyiSEyacBmoUzdARhivsIulFwsP9kdpg8okW9piDp87+gW6j1cUjG4G8iPwyUVgCYiQIqrtYGNCU1Y5ZM1eUwqsGgqYiRQwYkiTZz5yxwwymUIdSx60cO2tnmaLRs/ejKN+cGHb0Wk2+gc/FzoOO5CbTX0R82WBE38E+H1eVPgRV248iA47th+DpwMlGWtMpRRUs46Q9RbFeiMqBwPR8R9XS5IYp1XiHqa8gsHK3q96HZFNDLsVXLrBqFRzB3Untgd8wTbNgDe7wHU4dNWa2h+1VMSt2fBlQmb+IOk8CwR3A3Jvbk4deQ93yKSbbSq8GR7P+J5pWpOCo9yJ7ooPRIl13EZtcZDl3iPZ6dLwTG/q2sjrQzjJdwvcq4GpKp0Pl9XSmYaMxMiMeD6o6xWt8PPlWfG1pJfU+0OqMB+J2U0HdGie9OpweMBB0jcUcIdiMSTd8vIek7IwRqZIqT8Z8d5WfE9bsWTNxkOo3HCj8wO4dz4AZ8vODasmiOhkH6qP3nL7d4He/AUP4f0nx4+T8Bx5bK7TNka4o9N/KCYCQ/EcVvYiZ7xAx7BTPsPTFzZkfR9plZtTPXRxKQETPxqcrveW6GcjwiJrcXI/aIn6tvXY7GV9Wrt11Vo9CArx+pfZyi+fmujwnuysMPXexDFfQ84L44cBz745H1hhvpJW+ygh0BetVfSI8BXb4MKLyA8mwP2I+f8d+XrHzFqnvTESRCG6/7xrb17IFo10s22NSF3sOdaIdH7wrwJtLwDVr0+otea+GbQou9KfFJPI09EoQY3jgWQXfEItSawLUfhl4cJgnGJIKhuyCmVoPYC5IIx0mUkDjxoqeLDF57Mr7k2XFCTMbfDcyHsu5L4flXUEsHCMaf7I25BAAAWxQAAFBLAQIUABQACAAIANyplzvGn+yNuQQAAFsUAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA8wQAAAAA" framepossible="true" showreseticon="false" showanimationbutton="true" enablerightclick="false" errordialogsactive="true" enablelabeldrags="false" showmenubar="false" showtoolbar="false" showtoolbarhelp="false" showalgebrainput="false" /> | ||
<ggb_applet width="454" height="467" | <ggb_applet width="454" height="467" version="3.2" ggbbase64="UEsDBBQACAAIAEmWaj0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3V1tctu4Gf7dPQVHP/qjE3Px/TGNd8d2svly4iR2nOx2Ohlaom2uJdKRqETKDXqKXqG9Qg/QQ/QkfUGQsmRREmFbS1GTcSiBEAg87+cDAuTjn0e9rvc17A+iJN5tYR+1vDBuJ50ovthtDdPzHdX6+acfHl+EyUV41g+886TfC9LdFvVJy5QPo59++NPjwWXyzQu6WZXTKPy22zoPuoOw5Q2u+2HQGVyGYTpTHgxHUTcK+uOjs9/Ddjq4OWEbeRFfD+EqaX8IZe1e5zAaFF9/zC543Y3SJ9HXqBP2vW7S3m0JDl2HT6dhP43aQXe3xZAtIbstcuskFFFz9jLpR9+TODXVbxo/hxLPG0TfQ0CEmLLHP2YDfRwO292oEwWxGUzWD6jked+iTnoJF+QMmgyji0voKxPcttZOkn7neDxIw543+i3sJ9AdLH1CFKJEUDgISVve2J7CmviCY4oYQUIrzjGACD2GrhDhayUkoYhIyjFUgl8tPpddPPx6HKYpCHPgBaPwBuaLftSZ+fJisJ90b4qukyhOD4LrdNjPNIHmRcfp2FwOoOubYe7FF90wLyMgqMuwfXWWjI4tdNQ2fTK+zn6Sdejs4iDpJn2vb4TCoUJ+PLPHrI7p6aQWyuqgrEbehml0ch4Ay2pkxzN7zGp1o9h2LR85LkaNUXGZaOCZAmjcKPBk8N3gLASFaHnDOEoPiy+gOFf5ULH9wZth7wwsZ1p1Jm3ih2rz8Y+3lO7xVdiPw65VrRhkO0yGA++rUWF7rawjnbAd9eCrPZFDEhhxfYAO2NJOeNEPi45bu7OAZWfRtPrOFQ/SoA/ih2uk4DnsqZsuF100PRxAcTurlEapGamx/hQsb7fV8y/8ltcJUlNqzKsb9kKwvTTTmEzhJsj91po4miTzGYV3yM/fyABOl2pPpmdB9/oygBI/H0c3GIMHmR5Z1t7rpDM73mAyVDDka9OAEdh1GHZyr5nmWu5dQ5OZzUxJIwNx4I3shb1xfvxuf5tVseZl3El2WZrL3iKSIdnrBXHHi4MeXOcg6re7YQZJZFylFyADkRfg3RYvmkyGaXGqbZvLG5mDGsQUtSdQtluz9pNegprG4WCQGXk6bc6L5TE1+kUCQXcXR6XOgScO46/QtaQ/8LwRyiU1RgX8RckIUNuxksF50Xc8JRuQfD8aeXtF/b2i1h4Ekh3Cs480b3WPFY3t8fyT7c2X2PZ4YA0elKcdnUft5YJ+mxnBrJzbc+Ld+0yWC3jWlkz1OenNOqpyc8LEuuzsuCkmxe9qUrMQZc5xMv7//jtDCH44LHrtY8Qk1hJiMtaCa6lyG+hmWUgvivM+9ALolfCJolhxiiSWmisBQJ0Nku4wDY/b4Hbjw6Sdjb6wmzyJoCJrY2Tyl3xgjArz6TwahTcRujx1uZt/xGjeIHFFYWIHgwz67SlxLFQDhCXjlGjCsdYMPvAyvcBTejEVLBfY0fskhTBzy5CMHWQuE6TtBcR40DnLcrKrO8UowTIhmMOZPVS0qKPz80GYGlXZ0Zmi7JBl9nZjMczXkgikmRSKYSpkbj+cEMEIxYJSRYRk94lQR32I8RdJHHQPQTVuA29hH+1BujQHebAccqNpE0SDO4aqWWe33lh1g/sOvuWq5gXhEN1uxZOoB5yoHaV3SBxycZCSxKHjkjh0HkQaqzO57UgcCJ7PG0osM88i5mzzHknFizgFjgHju6UHHasHgXWGuEQd9t0Sjf27Jhp39onOXg9skkngzFBIhcASCPl93F5pnNkv4gyDXOUv//mXxXdvDt0DF2wPags2OAMOs2qwC58qoQhFVBPMmCAWduQrjbnEhAlEmSJSrg92ipfjvu+k07XhTmzwKOZ2VgFPfc4V1Vwb1AHgbL6oDHl6H+TfJt0xhPnyiLJvET+YQ/w0gvbaV9hWO/tzcJ0M/voZ2+pB9oFOyldJx3agwH/S9PpILOY0k6aZnLtj2oyWk5FBeGG+TTpyg1Ato7qzzwXnihnBlAtCJTW+d+J0Z8q5zTV3gDVpSsBVANfSCk49UEKUKV/XkIVJ7APGMT9tdhWG12a+8ig+6QfxwMx2357bqiqyoHHCYj5jSGmCtOIICSKe7mCRyYv4iihGjM+QTGCNrMsgkJUAV2PA0DRRAlKT5oqr8DXNEtm8IeEFBpYJTPpSYsa1gP+ElkhvsryqEPg8rUJT4X2ewz9xCe9PagvvykqucnRnkKtqrIAYaPCVwkZ3CPpaCK0RwgI8Kef3IvGnGQcqB/3JHM7D5ThbQjUBcrj5ZHHWzrSmWArCOBNUIZbDjSRDXAjFKQcpWO5wc6Eqo5u6w5KbVjvop+EgCuJ8+OZeSzYR7IWj68mc1CKhZabVXWgsw/k5rmpp1sxM15S3dHaE6yB3f4g5LEJ2fxGyT10wfVo7saiINfER10hCSqCB0gGZyHMErAhTnFGTwWGB+DqgPlgE9S8uUP9SF9TECWjmKyU54hDKwcMgtQ6gF/C33L4zsJ/awPrLQhY3Xbk9+WKY3OTLDZtbPYNUzufqzM/WxOrajcw5S1LLJZQOwJOME4YEo5IoOpm63MykcwWna6TAivuIC1gckG4MAkMYYa6NfB7qLkR9LC6fdm6OiMr42mIap32tFZMC2B4XVDeexj2pROOeuUT4Z7UlU3bGZKfi7DjyKVOQSlGhJDFzLspKnvnaFCPCMdEaE7yOZGomyluu97f88OSR9+zvf19EFe5MGDaNNtQK/1MH4J+7gP28PiaR3xuquBDB3BAXkMhiDIEHkoQCfqBtkgoESa/SRCAi7nWLYhH+vzjg/8IF/xd14W9Jr6wGPvalAOWGmI+RhtwMqzVgv5ReTLuf59btv1hBMqZ/cl5CNaYJR3if20dz/mpbSMd5I3NYN9IhfC7MHIWZoUAcbQHlaKTQVhEPbNZUSqEE0iBDInWD7x+FjZSQG++QPmcSvihECJESa77J8qpAPJ5VIh4vXWL/y9pyL+50/2iH+JqaCE8EZiBlUSS+iHGkmJZYSSbpvVblrOAdi9nHs0fey1Xs454cZNOYSJ3yeO4gg1cuiL+qm4ioiuAzn3KKqQYmqCiHGJXHLUGRkpiBz0PYLL9cB/ovHNA/dEH/sC70bdTXFbHHPjA/yA3MbTowALkG6CuwkGln9MpGgsNKXGT6h9FCRjLNSy4fipdsITuJGplGVc2iVD59qyDpVZQBReGYyo2evnVgJ40U3UKOYiPtjvQZw2azNhcQIoTSDeaSl42UkBtHgWgiGGVMcMQQoS7b0zaRobysxFBeu6QFrxuySw2SMsUxk0pQ4yR1vvwB+wTpbBuHKaNUr2WdycLcYDZNe/nIe12Spr35jF0k8iZfKrwZRKRO2F+5gOwEcX27ZZQTExE+EVxogjWVZvOwLDZtEMQEuDTFKPDANS1kO3SA/8gF/qNmUBHqm0UqEDqERghSNMHWgX45G3nzOd8N88Z6+aNF7CPf1NSd5hqxZRZX92AWNS2ZWBOP6DYy1XHjEcrnEguzdEcigiFJ3eRcZ7m44oYJagVrQCAZJcF5M4KkZlg0mDRcNdKS3EjDDvcxR1QhyTRGiNONpuQVaMPrSrThrUsIf1v3jY3qtIFpqqUhfwxcJS1+7mOzPYBLyF0Zp4qTdWRQkyg+m0O9fuS9Lcmh3rnxhHcbxhPqxNkFZSeM6yMK2m3tFPc1UlgBRzMb7DXNd/5RXyD4p4kGAqfYvZ5msAj9Iwf037ug/77elVOVsTf7vrTkQggNeZdkDw99OUl4V7iXd9anv19IEqbnLJJpqvDFUoX4PlRhC288JI1Mc9wIA/UJ50JhzhgwBy54g1f6f2mYpFYwBrMUSmuOQGpGcqK5gokbaUiOfEH7jHPIciTnZluw2OiFaxX4wttKfOHYJZQf/7GhfPnSGkSpUJSA5kiNUP4IIuZzISWRRCmQMBSvZU71XTkjePvIOy7Jlk7cGMHJRjGCenF2QdkJ4/oYAXfNShmTSgPYUnLzGBeLPxAFhTVDiiNu1tquZQ3Zewf4P7jA/6Eu+LHTXu0d5EM0Z0ILDipu9seTNaBfzgpOChdzYj33hxWsYJob9Ke5QWq5wZf7c4MtZAj9RiY2bgwBXAg3e7Q105wZRcYNnrlOGyaqVRRB+BociaJSAE3gCDeZvTXSlpxJAqVcgawE05Ig3PTdEseVSMKpS3A/rflpW5WdKJUKK0istFmLryktMluFzDplJrXQmOu1JLYn5QTi+JF3WpJbfXQjEB83iUDUC7MLyE4Q17cJgjgtPYKWqdnwK4HBKYWBp+UL9oRPCOLwZ15KxIRSa1n79cFBAJ9cBPCp5qc9VdyRRXypCUOIQjCBsAFkeR3olzOIj4WP+Wjd+qdKDGKaRwynecQ3yyPSh+IRW8gmho3MgBzZhPKzBFYiiammmjd4WvtbwyS1ikxIH+KoediypMrcq2+uZNJGWpIjl4AUiCmkBYGoLCjd7CcaVOASp5W4xK8uYf7Xhjy5l/kQ37GSSpBsmlYU62ak5lrAKUk5iH4tOdbHci5x+sj7tSTLOnDjEgebxCVqRdkB4z03jPdWYrzG2xHSZTE9IA3uSzKKzEYsjAsqRzDCUpnlM0QoitbC5T45CGDfTQD7dQrA6XYQ9zmEeATRhGMGSK9FAuV04qBwM3vFOz1ylMsoBbVVR9MEol28AuTbPSgE3SrCMGpkmlP2gKZljEH7CoPHxooyJoVgG71/c8XTfRv3ApBVnAHbFadYgfPAGOuNXiW/gs410ppKn3e2bC80yAsprSHTEZyxJm1rOM4FNhtY8lcczz2GdCaunC2PFnPPDH5gJWgncSeyLzSF6kd57Z73v3/80/ujXldR8vzS7LWTJU87dX5fRWMUY4F6hG7qEW6lesw9VWpc/giqrdKONyVJ6LmbNpxvoTaUbe0flz8IYKvU4V2JOly4qcPF9qlD2f6tcfl2r63ShpMSbbh004bL7dOGsrW74/KlvlulDR9LtCFy04ZoG7VhbiHGuHzZxvf8xdjboQ0HJdrwu5s2/L592lAylz4unXjfLmWYf3/0lZsqXG2fKpS9oD5/j8btd65vVZjYW8Axu24a0d1CjSh79eK4/EWNm68Ss+I7S5JuGNzcb+hl4oMfD8PZJtxvE91NDlP72FG+k10sFVNwnWlHVnac9sOzML49ZFDeeACdzOAz3y/C5CI86wc//R9QSwcIY1NEgSwPAAA1kgAAUEsBAhQAFAAIAAgASZZqPWNTRIEsDwAANZIAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABmDwAAAAA=" framepossible="false" showreseticon="true" showanimationbutton="true" enablerightclick="true" errordialogsactive="true" enablelabeldrags="false" showmenubar="false" showtoolbar="false" showtoolbarhelp="false" showalgebrainput="false" allowrescaling="true" /> | ||
__NOCACHE__ | |||
Wie GeoGebra-Übungen am sinnvollsten ins ZUM-Wiki eingebunden werden können, zeigt das folgende Video: | |||
== | :<iframe width="560" height="315" src="https://www.youtube.com/embed/Y2lR-yrf_XA" frameborder="0" allowfullscreen=""></iframe> | ||
==Anmerkungen== | |||
<references /> | |||
==Weblinks== | |||
*[http://www.geogebra.at/ GeoGebra (www.geogebra.org)] - Informationen, Download und mehr | |||
*[http://prezi.com/fueqbqynp5wf/geogebra-schilf/ GeoGebra-SchiLF (auf Prezi.com)] von [http://www.kurtsoeser.at/ Kurt Söser] - Kurze einführende Präsentation mit vielen Beispielen. Stand: 11. Mai 2011. | |||
[[Kategorie: | [[Kategorie:Mathematik]] | ||
Aktuelle Version vom 7. Mai 2022, 15:43 Uhr
GeoGebra ist eine dynamische Mathematik-Software, die Geometrie, Algebra und Analysis verbindet. Sie wurde für den Unterricht in den Sekundarstufen von Markus Hohenwarter ursprünglich an der Universität Salzburg entwickelt.[1]. Inzwischen ist GeoGebra ein internationales Projekt, das Unterstützung aus verschiedenen Ländern enthält.
Geogebra
- ist kostenlos und plattformunabhängig (siehe Java);
- muss nicht installiert werden, die aktuellste Version ist immer über den Webstart verfügbar;
- bietet die Möglichkeit, fertige Arbeitsflächen in eigene Internet-Seiten zu integrieren, sodass Arbeitsblätter im Internet-Browser bearbeitet werden können;
- bietet starke Algebra-Fähigkeiten;
- ist auch als Funktionsplotter einsetzbar.
- kann Grafiken komplett nach LaTeX exportieren.
Angebote auf der Homepage www.GeoGebra.org
- Es gibt ein GeoGebra-Wiki, das als Handbuch fungiert. Aus GeoGebra heraus weist die Hilfe immer auf eine Seite im Wiki, in der jeweiligen Sprache. Benutzer können eigene Beiträge leisten, indem sie Erläuterungen und Beispiele ergänzen. Dazu muss man sich im Wiki anmelden. Es gibt auch einige ergänzende Seite, wie etwa zu LaTeX
- Es gibt ein GeoGebra-Forum, in dem man Fragen bei Problemen stellen, Vorschläge für Neuerungen melden und Hinweise auf Fehler geben kann. Im deutschen Bereich gibt es einige erfahrene Anwender, die schnell und kompetent helfen können.Auch internationale Foren-Bereiche sind vorhanden!
- Es gibt die Material-Plattform geogebra.org, auf der man sein Material unter einer CC-BY-SA Lizenz veröffentlichen kann. Aufgrund der Lizenz können Sie auch das Material von anderen kopieren und verändern. GeoGebraTube bietet außerdem die Möglichkeit die Zeichnungen in HTML5 auf mobilen Geräten anzeigen zu lassen, Material von anderen zu nutzen und sie zu GeoGebraBooks zu verbinden. Auf GeoGebraTube hochgeladene Zeichnungen (egal ob von Ihnen oder einem anderen Benutzer) können in das ZUM-Wiki eingebunden werden.
Fähigkeiten von GeoGebra
Neueste Version von GeoGebra
Die am 1. Dezember 2013 erschienene Version 4.4 weist ein paar kleine Änderungen auf. Mehr dazu in den Release-Notes.
Zukunft von GeoGebra
Die nächste größere Änderung wird in der Version 5.0 die Einführung einer 3D-Ansicht sein. Eine Beta-Version ist zum Testen verfügbar und hat bereits beachtlich Fähigkeiten. Mehr dazu in den Release-Notes, die aber noch erweitert werden.
Die Seite GeoGebra3D - Anwendung in der Linearen Algebra auf dem Wiki der GeoGebra-Instituts Landau (Rheinland-Pfalz) enthält einige Informationen für Anfänger, mit Anleitungsvideos und Übungsaufgaben.
Einsatzmöglichkeiten
… als interaktives Geometrie-Programm:
Hier hat GeoGebra inzwischen die Konkurrenz mehr als eingeholt. Es bietet nicht nur die üblichen Zeichenfunktionen, sondern es können auch selber Werkzeuge definiert werden und Animationen sind mit Hilfe von Schiebereglern möglich.
Der Wenn-Befehl ermöglicht eine Zeichnung für verschiedene Situationen verwendbar zu machen.
- Beispiel: Verschiebt man ein Parallelogramm kann die Höhe nicht immer an die gleiche Stelle eingezeichnet werden. Man kann bei GeoGebra mit dem Wenn-Befehl testen, ob ein Punkt definiert ist und ihn dann zum Höhenfußpunkt machen oder als Alternative einen anderen.
- H = Wenn[IstDefiniert[H1],H1,H2]
- Wenn H1 definiert ist, dann soll H dem Punkt H1 entsprechen (der unsichtbar sein kann!), ansonsten soll H gleich H2 sein.
Ist für eine Zeichnung eine unbestimmte oder dynamisch festgelegt Anzahl an Objekten nötig, so kann man den Befehl Folge verwenden.
- Beispiel: Eine Strecke zwischen den Punkte A und B soll in n Teile zerlegt werden, wobei die Zahl n durch einen Schieberegler bestimmt wird.
- Trennpunkte=Folge[A+i*(B-A)/n,i,1,(n-1)]
- Es wird hier quasi mit Vektoren gearbeitet und zu A immer wieder ein Vielfaches des um den Faktor 1/n verkürzten Vektors AB dazu addiert.
Weitere Besonderheiten:
- Zufallszahlen ermöglichen das Erstellen von immer wieder neuen Aufgabenstellungen.
- Mit Kontrollästchen können Teile der Zeichnung unsichtbar gemacht werden. Tipp: Kombiniert man "Wenn" mit Kontrollkästchen, können Ausgangsbedingungen einer Zeichnung über ein Kontrollkästchen festgelegt werden.
... als Funktionsplotter
Geogebra ist als Funktionenplotter für die Sekundarstufen I und II geeignet:
- Parameter können mit der Maus oder den Pfeiltasten stufenweise verändert werden.
- Der Funktionsterm wird beim Verschieben des Graphen (mit Maus oder Pfeiltasten) automatisch angepasst.
- Kurvenscharen können animiert und die "Spuren" angezeigt werden.
- Ableitungen und Flächen unter Graphen können dargestellt und berechnet werden.
Zeichenaufgaben können auf fast natürlich mathematische Weise erledigt werden. Zwingend ist dabei die Nutzung der Funktionsdefinition möglich und bietet, richtig angewandt, die Möglichkeit den Schülern zu verdeutlichen, wie und warum man die Funktionsschreibweise verwendet.
- Beispiel: Zeichne den Punkt auf der Funktion bei x = 2
- P=(2,f(2))
- Hier zeigt sich schön, woher der y-Wert kommt.
- P=(2,f(2))
- Beispiel für ein GeoGebra-Applet
Die Datei [INVALID] wurde nicht gefunden.
- Das schreibt man
<ggb_applet height="650" width="800" showMenuBar="true" showResetIcon="true" filename="Graph_Rauchen.ggb" />
… als Tabellenkalkulation
Seit der Version 3.2 bietet GeoGebra eine Tabelle mit den grundlegenden Fähigkeiten einer Tabellenkalkulation wie Calc und Excel:
- Autovervollständigung bei Zahlen.
- Man kann Rechenformeln und Text eingeben.
- Formeln kennen absolute und relative Adressierung und können kopiert werden.
- Bereich können markiert und erfasst werden.
Speziell in GeoGebra vorhanden sind zusätzlich noch die folgenden Fähigkeiten:
- Jede Zelle kann jede Art von Objekt enthalten, also auch Strecken, Integral, Funktion usw. und es sind damit alle üblichen Rechenfunktionen verwendbar. Auch hier wird die Adressierung beachtet.
- Zeichen-Objekte aus der Tabelle werden direkt angezeigt
- Aus Zelleninhalten können Listen und Matrizen erstellt werden.
- In Formeln können auch alle Werte aus GeoGebra verwendet werden, wie Schiebregler und Funktionen.
Dank diese Tabelle kann man nun auf dein Einsatz reiner Tabellenkalkulationsprogramme verzichten und hat gleichzeitig noch die Zeichenfähigkeit, wie sie in Tabellenkalkulationsprogrammen nicht vorhanden sind. Auch ein Diagramm-Editor kann da bei weitem nicht mithalten!
Neben den üblichen Anwendungen, wie Zuordnungen und Wertetabellen, kann man auch Folgen (explizit und rekursiv) berechnen lassen. Ein weitere Idee zur Anwendung in der Analysis sind die diversen Näherungverfahren, die rekursiv ablaufen.
GeoGebra im Unterricht
- GeoGebra-Wiki mit Unterrichtsmaterialien und und Arbeitsblättern zum Download.
- www.realmath.de - zahlreiche Beispiele, die zeigen, wie GeoGebra im Unterricht eingesetzt werden kann.
- Private Sammlung von Arbeitsblättern, die GeoGebra nutzen. Es wird Wert darauf gelegt, dass es nicht nur Aufgabenblätter sind, die "eine" Antwort erwarten. Es soll geforscht werden.
Video-Hilfen
Einsatzgebiete außerhalb der Mathematik
- Informatik: Turtlegrafik in Geogebra - Realisierung einer rudimentären Turtlegrafik mit geogebra auf Grundlage eines Objektes Schildkroete. (JavaScript)
- Wirtschaft: Gleichgewichtspreis - Interaktive Animation
GeoGebra-Dateien im ZUM-Wiki
GeoGebra-Dateien (mit der Dateiendung .ggb) können ins ZUM-Wiki und in jedes Wiki der Wiki-Family hochgeladen werden.
Hochgeladene ggb-Dateien können dann entweder intern verlinkt werden oder direkt angezeigt werden, wie die folgenden Beispiele zeigen:


Wie GeoGebra-Übungen am sinnvollsten ins ZUM-Wiki eingebunden werden können, zeigt das folgende Video:
Anmerkungen
Weblinks
- GeoGebra (www.geogebra.org) - Informationen, Download und mehr
- GeoGebra-SchiLF (auf Prezi.com) von Kurt Söser - Kurze einführende Präsentation mit vielen Beispielen. Stand: 11. Mai 2011.