Grundlagen der Achsenspiegelung: Unterschied zwischen den Versionen
Main>Laura Klaus Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (34 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
{{ | {{Box|1=Grundlagen der Achsenspiegelung|2= | ||
[[Datei:Mount Hood - Wasserspiegelung.jpg|right|250px]] | |||
In diesem Lernpfad soll es um das Thema Achsenspiegelung gehen. Wir wollen herausfinden, was eine Achsenspiegelung ist und wie man eine Figur spiegeln kann. Dabei wollen wir wichtige Begriffe kennenlernen. | |||
Übertrage alle Merksätze und Definitionen in dein Heft! | |||
[[ | |||
'''Viel Spaß beim Bearbeiten des Lernpfads!''' | '''Viel Spaß beim Bearbeiten des Lernpfads!''' | ||
;Zeitbedarf | |||
:45 Min. | |||
;Material | |||
:dein Heft, Stifte und ein Geodreieck | |||
[[Datei:Logo Mathematik-digital 2011.png|200px|left|verweis=Mathematik-digital]] | |||
|3=Lernpfad}} | |||
{{Navigation verstecken|{{Vorlage:Achsenspiegelung}}}} | |||
[[Bild:Spiegel5.jpg|400px]] | |||
=1.Station: Was ist eine Achsenspiegelung?= | =1.Station: Was ist eine Achsenspiegelung?= | ||
Wie kann man eine Figur ohne einen Spiegel spiegeln? Hier siehst du zwei Möglichkeiten, wie das geht. | Wie kann man eine Figur ohne einen Spiegel spiegeln? Hier siehst du zwei Möglichkeiten, wie das geht. | ||
{{Box|1=1.Möglichkeit: Klecksbilder|2= | |||
[[Bild:Klecksbild1.jpg|400px]] [[Bild:Klecksbild2.jpg|400px]] | [[Bild:Klecksbild1.jpg|400px]] [[Bild:Klecksbild2.jpg|400px]] | ||
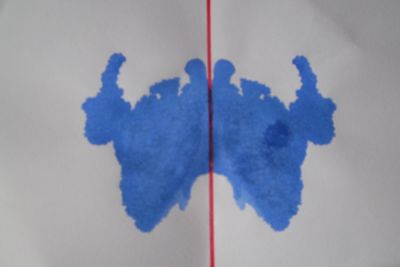
So ein Klecksbild kannst du ganz einfach zu Hause nachmachen. | So ein Klecksbild kannst du ganz einfach zu Hause nachmachen. | ||
Um es herzustellen, brauchst du ein Blatt Papier und Tinte. | Um es herzustellen, brauchst du ein Blatt Papier und Tinte. | ||
'''1.Schritt:''' Falte das Blatt Papier in der Mitte zusammen und dann wieder auf. | '''1.Schritt:''' Falte das Blatt Papier in der Mitte zusammen und dann wieder auf. | ||
'''2.Schritt:''' Nun gibst du einige Tropfen Tinte auf die eine Hälfte des Blattes. | '''2.Schritt:''' Nun gibst du einige Tropfen Tinte auf die eine Hälfte des Blattes. | ||
'''3.Schritt:''' Jetzt musst du das Blatt wieder zusammenfalten und glatt streichen. | '''3.Schritt:''' Jetzt musst du das Blatt wieder zusammenfalten und glatt streichen. | ||
'''4.Schritt:''' Wenn du das Blatt wieder auffaltest, siehst du dein Klecksbild. | '''4.Schritt:''' Wenn du das Blatt wieder auffaltest, siehst du dein Klecksbild. | ||
'''5.Schritt:''' Die Faltlinie in der Mitte des Blattes kannst du farbig kennzeichnen. | '''5.Schritt:''' Die Faltlinie in der Mitte des Blattes kannst du farbig kennzeichnen. | ||
|3=Unterrichtsidee}} | |||
{{Box|1=2.Möglichkeit: Durchstechen mit einer Nadel|2= | |||
[[Bild:Durchstechen.png|600px|center]] | [[Bild:Durchstechen.png|600px|center]] | ||
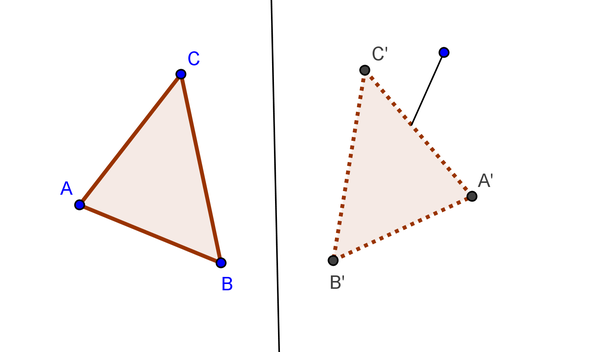
Auch dieses Verfahren kannst du leicht ausprobieren. Dazu benötigst du wieder ein Blatt Papier und eine Stecknadel. | Auch dieses Verfahren kannst du leicht ausprobieren. Dazu benötigst du wieder ein Blatt Papier und eine Stecknadel. | ||
'''1.Schritt:''' Als erstes musst du das Blatt wieder in der Mitte falten und anschließend öffnen. | '''1.Schritt:''' Als erstes musst du das Blatt wieder in der Mitte falten und anschließend öffnen. | ||
'''2.Schritt:''' Nun zeichnest du ein beliebiges Dreieck auf die eine Hälfte des Blattes. | '''2.Schritt:''' Nun zeichnest du ein beliebiges Dreieck auf die eine Hälfte des Blattes. | ||
'''3. Schritt:''' Jetzt faltest du das Blatt wieder zusammen. Dabei muss das Dreieck jedoch nach außen (zu dir) zeigen. | '''3. Schritt:''' Jetzt faltest du das Blatt wieder zusammen. Dabei muss das Dreieck jedoch nach außen (zu dir) zeigen. | ||
'''4.Schritt:''' Als nächstes stichst du mit Hilfe der Nadel durch die Eckpunkte des Dreiecks und entlang der Linien. | '''4.Schritt:''' Als nächstes stichst du mit Hilfe der Nadel durch die Eckpunkte des Dreiecks und entlang der Linien. | ||
'''5.Schritt:''' Wenn du das Blatt wieder öffnest, siehst du auf der | '''5.Schritt:''' Wenn du das Blatt wieder öffnest, siehst du auf der zweiten Hälfte des Blattes das Abbild deines Dreiecks. | ||
'''6.Schritt:''' Als letztes kannst du die Mittellinie wieder farbig kennzeichnen und die durchstochenen Punkte mit einem Stift verbinden. | '''6.Schritt:''' Als letztes kannst du die Mittellinie wieder farbig kennzeichnen und die durchstochenen Punkte mit einem Stift verbinden. | ||
|3=Unterrichtsidee}} | |||
'''Mit diesen beiden Verfahren kannst du mit wenigen Werkzeugen ein Spiegelbild erzeugen.''' | |||
[[Bild:Spiegel11.jpg|400px|center]] | |||
{{Box|1=Ordne die Begriffe richtig!|2= | |||
Ordne die Begriffe den Lücken zu. Ziehe dabei mit der linken Maustaste an ihnen und lasse sie fallen, wenn die Lücke rot wird. | Ordne die Begriffe den Lücken zu. Ziehe dabei mit der linken Maustaste an ihnen und lasse sie fallen, wenn die Lücke rot wird. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Das Dreieck, von dem du beim Durchstechen ausgehst, heißt '''Urfigur'''. Das Dreieck, das beim Spiegeln entsteht, wird als '''Bildfigur''' bezeichnet. Urfigur und Bildfigur sind '''symmetrisch''' zueinander. Legt man die beiden Dreiecke übereinander, dann überdecken sie sich vollständig, d.h. sie sind '''deckungsgleich'''. Die Faltlinie heißt '''Spiegelachse'''. Das Verfahren, durch das die Bildfigur ensteht, nennt man '''Abbildung'''. Dabei wird jedem '''Urpunkt''' genau ein '''Bildpunkt''' zugeordnet. | |||
</div> | |||
Konntest du alle Begriffe richtig zuordnen? Super! Ansonsten versuchs noch einmal. | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Merke|2= | |||
[[Bild:Spiegel_Achsensp.jpg|200px|right]] | |||
'''Wichtige Begriffe''' | |||
''' | |||
*Die Ausgangsfigur bei einer Abbildung heißt '''Urfigur''' oder '''Originalfigur'''. | |||
*Die Ausgangsfigur bei einer Abbildung heißt '''Urfigur''' oder '''Originalfigur'''. | |||
*Die entstandene Figur nennt man '''Bildfigur'''. | *Die entstandene Figur nennt man '''Bildfigur'''. | ||
*Urfigur und Bildfigur sind '''deckungsgleich''' zueinander. Ein anderes Wort für deckungsgleich ist '''kongruent'''. | *Urfigur und Bildfigur sind '''deckungsgleich''' zueinander. Ein anderes Wort für deckungsgleich ist '''kongruent'''. | ||
*Bei einer Abbildung wird jedem '''Urpunkt''' genau ein '''Bildpunkt zugeordnet'''. | *Bei einer Abbildung wird jedem '''Urpunkt''' genau ein '''Bildpunkt zugeordnet'''. | ||
*Die Gerade an der gespiegelt wird heißt '''Spiegelachse''' oder '''Symmetrieachse'''. | *Die Gerade, an der gespiegelt wird, heißt '''Spiegelachse''' oder '''Symmetrieachse'''. | ||
|3=Merksatz}} | |||
}} | |||
{{Box|1=Löse den Lücktext und das Schüttelquiz|2= | |||
[[Bild:Spiegel6.jpg|200px|center]] | |||
[[Bild:SpiegliNamen.png|center]] | |||
[[Bild:Spiegel6.jpg| | |||
Ordne die Wörter den richtigen Lücken zu! | |||
[[Bild:SpiegliNamen.png | |||
Ordne die Wörter | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
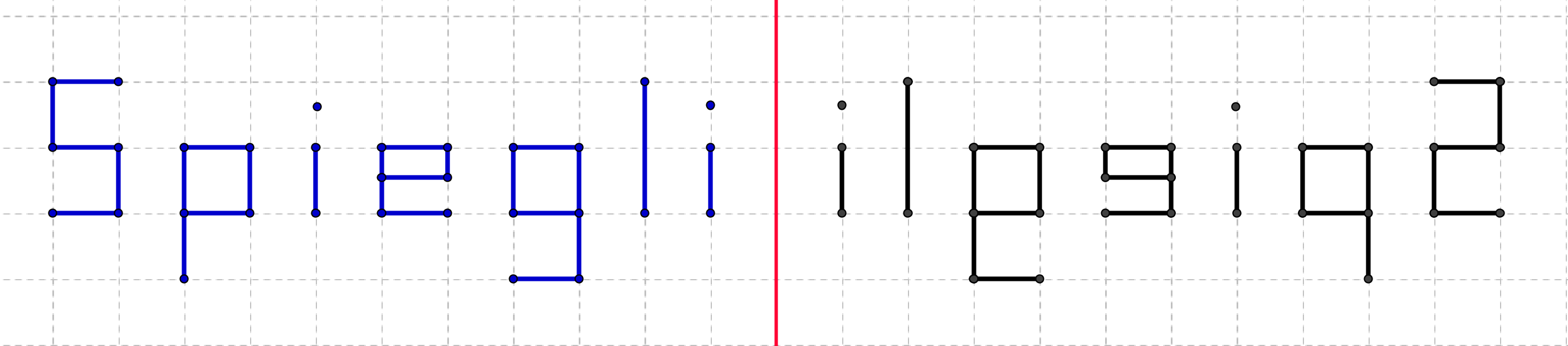
Mein Name ist '''spiegelverkehrt''' zum blauen Original. Das heißt die Buchstaben sind in '''umgekehrter''' Reihenfolge angeordnet. | Mein Name ist '''spiegelverkehrt''' zum blauen Original. Das heißt die Buchstaben sind in '''umgekehrter''' Reihenfolge angeordnet. | ||
Bei der Spiegelung hat sich also der '''Orientierungssinn''' geändert. Mein gespiegelter Name ist daher '''gegensinnig''' kongruent. | Bei der Spiegelung hat sich also der '''Orientierungssinn''' geändert. Mein gespiegelter Name ist daher '''gegensinnig''' kongruent. | ||
</div> | |||
Es gibt aber nicht nur Unterschiede zu meinem Originalnamen. | Es gibt aber nicht nur Unterschiede zu meinem Originalnamen. | ||
Versuche die verschüttelten Buchstaben richtig zu ordnen und die Wörter richtig zu entschlüsseln! | |||
Versuche die | Schreibe das richtige Wort in die Lücke. | ||
<div class="schuettel-quiz"> | <div class="schuettel-quiz"> | ||
Die Buchstaben haben trotzdem dieselbe '''Höhe''' und eine unveränderte '''Breite'''. | Die Buchstaben haben trotzdem dieselbe '''Höhe''' und eine unveränderte '''Breite'''. | ||
Außerdem besitzen sie immer noch die gleiche '''Form'''. | Außerdem besitzen sie immer noch die gleiche '''Form'''. | ||
</div> | </div> | ||
Wenn du alle Wörter richtig entschlüsseln konntest, versuche deinen Namen zu spiegeln. | Wenn du alle Wörter richtig entschlüsseln konntest, versuche deinen Namen zu spiegeln. | ||
|3=Arbeitsmethode}} | |||
{{Box|Definition| | |||
Eine Abbildung, bei der die Urfigur an einer Spiegelachse gespiegelt wird, heißt '''Achsenspiegelung''' | |||
|Merksatz}} | |||
{{Box|1=Winkel und Strecken zur Spiegelachse|2= | |||
''' | Sieh dir das Urbild und das Spiegelbild des Männchens genau an. Achte dabei auf die Abstände der Urpunkte zur Spiegelachse. Vergleiche sie dann mit den Abständen der Bildpunkte zur Spiegelachse. Was fällt dir dabei auf? | ||
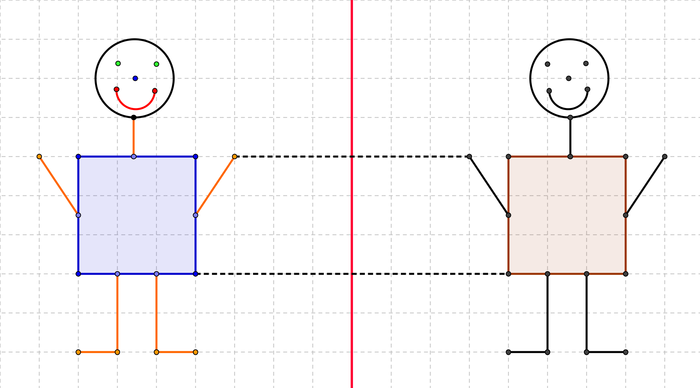
Sieh dir das Urbild und das Spiegelbild des Männchens genau an. Achte dabei auf die Abstände der Urpunkte zur Spiegelachse. Vergleiche sie dann mit den Abständen der Bildpunkte zur Spiegelachse. Was fällt dir dabei auf? | |||
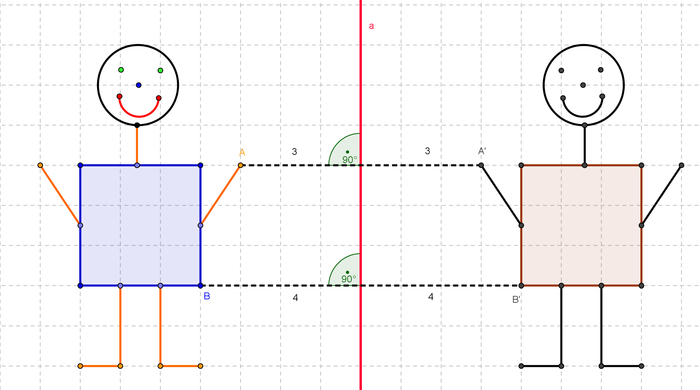
Betrachte dann auch die Strecke zwischen einem Urpunkt und dessen Bildpunkt. Wie verhält sich diese Strecke zur Spiegelachse? | Betrachte dann auch die Strecke zwischen einem Urpunkt und dessen Bildpunkt. Wie verhält sich diese Strecke zur Spiegelachse? | ||
[[Bild:Männchen.png|700px|center]] | [[Bild:Männchen.png|700px|center]] | ||
[[Bild:Männchen1.png|700px|center]] | |||
{{Lösung versteckt|1=[[Bild:Männchen1.png|700px|center]] | |||
Du siehst, dass ein Urpunkt denselben Abstand zur Spiegelachse hat, wie ein Bildpunkt zur Spiegelachse, hier z.B. 3LE. | Du siehst, dass ein Urpunkt denselben Abstand zur Spiegelachse hat, wie ein Bildpunkt zur Spiegelachse, hier z.B. 3LE. | ||
Die Verbindungsstrecke zwischen dem Urpunkt und dem Bildpunkt ist senkrecht zur Spieglachse a. | Die Verbindungsstrecke zwischen dem Urpunkt und dem Bildpunkt ist senkrecht zur Spieglachse a.|2=Lösung anzeigen|3=Lösung verstecken}} | ||
}} | |3=Arbeitsmethode}} | ||
'''Wir wollen nochmal zusammenfassen, was wir bis jetzt gelernt haben.''' | '''Wir wollen nochmal zusammenfassen, was wir bis jetzt gelernt haben.''' | ||
{{Merke|'''Achsenspiegelung''' <br> | {{Box|1=Merke|2= | ||
* Die Achsenspiegelung ist eine Abbildung, bei der jedem Urpunkt genau ein Bildpunkt zugeordnet wird. | [[Bild:Spiegel2.jpg|200px|right]] | ||
'''Achsenspiegelung''' <br> | |||
* Die '''Achsenspiegelung''' ist eine Abbildung, bei der '''jedem Urpunkt genau ein Bildpunkt''' zugeordnet wird. | |||
* Dabei wird ein Urpunkt z.B. mit A, B, C,... bezeichnet, ein Bildpunkt mit A', B', C',...(Lies: A Strich). | * Dabei wird ein Urpunkt z.B. mit A, B, C,... bezeichnet, ein Bildpunkt mit A', B', C',...(Lies: A Strich). | ||
* Der Urpunkt und der Bildpunkt sind gleich weit von der Spiegelachse entfernt, d.h. die Spiegelachse halbiert die Strecke zwischen Urpunkt und Bildpunkt. | * Der '''Urpunkt und der Bildpunkt sind gleich weit von der Spiegelachse entfernt''', d.h. die Spiegelachse halbiert die Strecke zwischen Urpunkt und Bildpunkt. | ||
* Die Spiegelachse ist eine Gerade und wird meist mit einem Kleinbuchstaben, z.B. a, versehen. | * Die Spiegelachse ist eine Gerade und wird meist mit einem Kleinbuchstaben, z.B. a, versehen. | ||
* Bei einer Achsenspiegelung ist die Verbindungsstrecke zwischen Ur- und Bildpunk immer senkrecht zur Spiegelachse. | * Bei einer Achsenspiegelung ist die '''Verbindungsstrecke zwischen Ur- und Bildpunk immer senkrecht zur Spiegelachse'''. | ||
* Außerdem ändert sich bei der Achsenspiegelung der Orientierungssinn der Urfigur, d.h. Urfigur und Bildfigur sind gegensinnig kongruent. | * Außerdem ändert sich bei der Achsenspiegelung der Orientierungssinn der Urfigur, d.h. Urfigur und Bildfigur sind '''gegensinnig kongruent'''.|3=Merksatz}} | ||
=2.Station: Achsenspiegelung durch Konstruktion= | =2.Station: Achsenspiegelung durch Konstruktion= | ||
Natürlich kannst du eine Achsenspiegelung nicht nur über Klecksbilder oder mit Hilfe einer Nadel erzeugen. Viel einfacher lässt sich eine Achsenspiegelung mit Hilfe des Geodreiecks konstruieren. | |||
{| style="margin:1em 1em 1em 0; border:solid 1px #AAAAAA; border-collapse:collapse; background-color:#F9F9F9; empty-cells:show; font-size:95%" rules="all" cellspacing="0" cellpadding="4" {{Prettytable}} | |||
|- | |||
!Schritt 1!! | |||
|- | |||
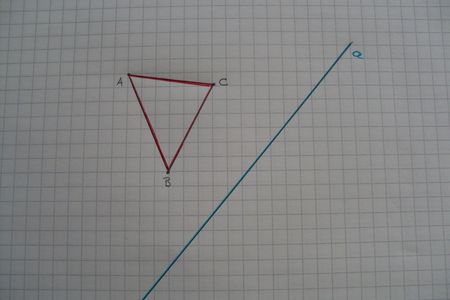
|- | |[[Bild:Schritt1.jpg|450px]]|| |Hier siehst du ein Dreieck ABC und die Spiegelachse a, an der das Dreieck gespiegelt werden soll. | ||
! Schritt | |- | ||
!Schritt 2!! | |||
|- | |||
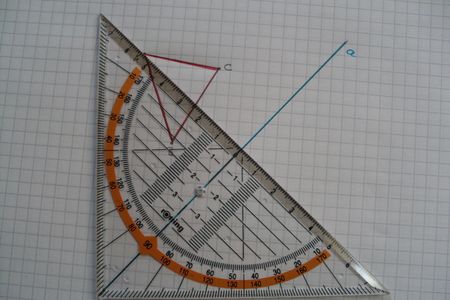
|[[Bild:Schritt2.jpg|450px]]|| |Jetzt musst du das Geodreieck so an die Spiegelachse legen, dass die Mittellinie des Geodreiecks sie überdeckt. Als erstes wird der Punkt A gespiegelt, daher musst du das Geodreieck an diesen Punkt anlegen. | |||
|- | |||
!Schritt 3!! | |||
|- | |- | ||
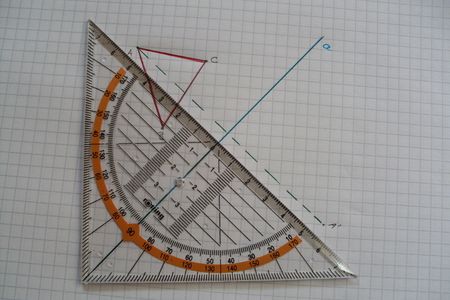
| [[Bild: | |[[Bild:Schritt3.jpg|450px]]|| |Als nächstes ziehst du eine senkrechte Hilfslinie zur Spiegelachse durch den Punkt A. Diese Linie hilft dir den Bildpunkt A' zu finden. Wie du bereits weißt, befindet er sich im gleichen Abstand zur Spiegelachse wie der Urpunkt. Du musst also die Länge zwischen A und der Spiegelachse messen und übertragen. Diesen Schritt wiederholst du dann für die Punkte B und C. | ||
|- | |- | ||
!Schritt 4!! | |||
! Schritt | |||
|- | |- | ||
| [[Bild: | |[[Bild:Schritt5.jpg|450px]]|| |Als letztes musst du die Bildpunkte A', B' und C' verbinden. Du erhälst damit das gespiegelte Dreieck A'B'C'. | ||
|} | |} | ||
{| | Die Konstruktion der Achsenspiegelung wird noch genauer, wenn du sie mit einem Geodreieck und einem Zirkel durchführst. | ||
{| style="margin:1em 1em 1em 0; border:solid 1px #AAAAAA; border-collapse:collapse; background-color:#F9F9F9; empty-cells:show; font-size:95%" rules="all" cellspacing="0" cellpadding="4" {{Prettytable}} | |||
! | !Konstruktion mit dem Zirkel!! | ||
|- | |- | ||
| [[Bild: | |[[Bild:Zirkel1.jpg|450px]]|| |Auch hier ist wieder ein Dreieck ABC und die Spiegelachse vorgegeben. Nun zeichnest du dir wieder die senkrechten Hilfslinien ein. Der Abstand zwischen Spiegelachse und Punkt wird aber jetzt nicht mehr mit dem Geodreieck abgetragen, sondern mit dem Zirkel. Dazu stichst du mit dem Zirkel in den Schnittpunkt von Spiegelachse und Hilfslinie ein, hier M<sub>1</sub>. Als Radius nimmst du die Strecke zwischen A und M<sub>1</sub>. | ||
< | |||
|- | |- | ||
!Konstruktion mit dem Zirkel!! | |||
! Konstruktion mit dem Zirkel !! | |||
|- | |- | ||
| [[Bild:Zirkel2.jpg|450px]]|| |Im nächsten Schritt ziehst du den Kreis um M<sub>1</sub>. Der Schnittpunkt des Kreises mit der Hilfslinie ergibt den Bildpunkt A'. Für die Punkte B und C verfährst du genauso. Zum Schluss musst du wieder die Bildpunkte zum Dreieck A'B'C' verbinden. | |[[Bild:Zirkel2.jpg|450px]]|| |Im nächsten Schritt ziehst du den Kreis um M<sub>1</sub>. Der Schnittpunkt des Kreises mit der Hilfslinie ergibt den Bildpunkt A'. Für die Punkte B und C verfährst du genauso. Zum Schluss musst du wieder die Bildpunkte zum Dreieck A'B'C' verbinden. | ||
|} | |} | ||
{{Box|1=Spiegelung mit Geogebra-Applet|2= | |||
Hier kannst du die Schritte einer Achsenspiegelung nochmal selbst nachvollziehen. Dafür musst du die Kästchen nacheinander anklicken. Wenn du in der rechten oberen Ecke auf die Pfeile drückst, kannst du von neuem beginnen. Viel Spass beim Ausprobieren! | Hier kannst du die Schritte einer Achsenspiegelung nochmal selbst nachvollziehen. Dafür musst du die Kästchen nacheinander anklicken. Wenn du in der rechten oberen Ecke auf die Pfeile drückst, kannst du von neuem beginnen. Viel Spass beim Ausprobieren! | ||
<ggb_applet height="450" width="850" showResetIcon="true" | |||
< | <ggb_applet height="450" width="850" showResetIcon="true" id="fc8ne5b4" /> | ||
<br> | |||
< | <br><br> | ||
<ggb_applet height="450" width="850" showResetIcon="true" id="pcmdhwpx" /> | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Achsenspiegelung auf Papier|2= | |||
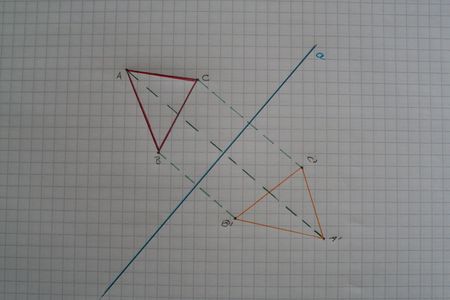
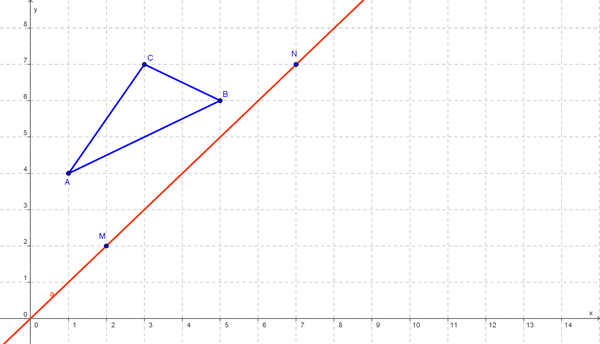
Übertrage folgende Aufgabenstellung in dein Heft und löse sie zu Hause. | Übertrage folgende Aufgabenstellung in dein Heft und löse sie zu Hause. | ||
Gegeben sind die Punkte M(2 | Gegeben sind die Punkte M(2{{!}}2) und N (7{{!}}7). Die Gerade a=MN sei die Spiegelachse. | ||
Spiegel das Dreieck ABC mit den Koordinaten A (1 | Spiegel das Dreieck ABC mit den Koordinaten A (1{{!}}4), B (5{{!}}6) und C (3{{!}}7) an a. | ||
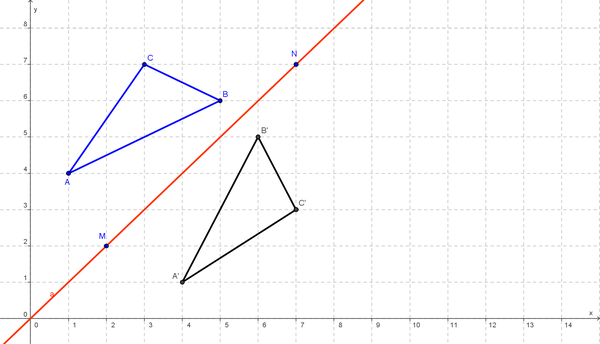
Notiere dir die Koordinaten der Spiegelpunkte in dein Heft! | Notiere dir die Koordinaten der Spiegelpunkte in dein Heft! | ||
[[Bild:Gitter.png|600px|center]] | [[Bild:Gitter.png|600px|center]] | ||
[[Bild:Gitter1.png|600px|center]] | {{Lösung versteckt|1=[[Bild:Gitter1.png|600px|center]]|2=Lösung anzeigen|3=Lösung verstecken}} | ||
}} | |3=Arbeitsmethode}} | ||
=3.Station:Übungen= | =3.Station:Übungen= | ||
{{Box|1=Richtig oder Falsch?|2= | |||
Wende jetzt dein Wissen über die Achsenspiegelung auf die folgende Aufgabe an. Kreuze jeweils Richtig oder Falsch an. | Wende jetzt dein Wissen über die Achsenspiegelung auf die folgende Aufgabe an. Kreuze jeweils Richtig oder Falsch an. | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 263: | Zeile 235: | ||
|| Nein! Kongruent heißt deckungsgleich. Bei der Achsenspiegelung überdecken sich Ur- und Bildfigur, wenn man sie übereinander legt. | || Nein! Kongruent heißt deckungsgleich. Bei der Achsenspiegelung überdecken sich Ur- und Bildfigur, wenn man sie übereinander legt. | ||
</quiz> | </quiz> | ||
|3=Üben}} | |||
{{Box|1=Das ist richtig so!|2= | |||
Du siehst hier das Bild eines Krankenwagens. Die Schrift ist mit Absicht so auf den Krankenwagen geklebt worden. Kannst du dir denken, warum die Aufschrift "Rettungsdienst" spiegelverkehrt ist? | |||
Du siehst hier das Bild eines Krankenwagens. Kannst du dir denken, warum die Aufschrift "Rettungsdienst" spiegelverkehrt ist? | |||
[[Bild:Krankenwagen.jpg|300px|center]] | [[Bild:Krankenwagen.jpg|300px|center]] | ||
Wenn | {{Lösung versteckt|1= | ||
}} | Wenn ein Autofahrer vor dem Krankenwagen fährt und in den Rückspiegel schaut, kann er die Schrift richtigherum lesen. Die spiegelverkehrte Schrift soll dem Krankenwagen helfen, im Notfall schneller im Straßenverkehr berücksichtigt zu werden. Der Fahrer muss sich also nicht erst anstrengen, um lesen zu können, wer hinter ihm fährt.|2=Lösung anzeigen|3=Lösung verstecken}} | ||
|3=Üben}} | |||
{{Box|1=Bonus|2= | |||
Wer ganz besonders schnell war, darf sich jetzt belohnen. Hier findest du den Link zu einem Spiel, bei dem es um die Achsenspiegelung geht. Du siehst Landschaften, die in der Mitte geteilt sind. Auf der rechten Seite sind jeweils ein paar Fehler im Vordergrund eingebaut. Also musst du diese Seite anpassen. Dabei steigert sich jedesmal die Anzahl der Fehler. Du hast aber immer nur wenige Sekunden Zeit, um die Fehler zu finden. Daher musst du schnell sein. Viel Spaß beim Spielen! | |||
Wer ganz besonders schnell war, darf sich jetzt belohnen. Hier findest du den Link zu einem Spiel, bei dem es um die Achsenspiegelung geht. Du siehst Landschaften, die in der Mitte geteilt sind. Auf der | |||
[http://www.miniclip.com/games/storybook/de/ Storybook] | [http://www.miniclip.com/games/storybook/de/ Storybook] | ||
|3=Üben}} | |||
[[Bild:Spiegel10.jpg|400px|center]] | [[Bild:Spiegel10.jpg|400px|center]] | ||
{{Fortsetzung | |||
|weiter=Eigenschaften der Achsenspiegelung | |||
|weiterlink=Eigenschaften der Achsenspiegelung}} | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Sekundarstufe_1]] | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:Geometrie]] | |||
Aktuelle Version vom 24. April 2022, 10:22 Uhr
In diesem Lernpfad soll es um das Thema Achsenspiegelung gehen. Wir wollen herausfinden, was eine Achsenspiegelung ist und wie man eine Figur spiegeln kann. Dabei wollen wir wichtige Begriffe kennenlernen.
Übertrage alle Merksätze und Definitionen in dein Heft!
Viel Spaß beim Bearbeiten des Lernpfads!
- Zeitbedarf
- 45 Min.
- Material
- dein Heft, Stifte und ein Geodreieck
1.Station: Was ist eine Achsenspiegelung?
Wie kann man eine Figur ohne einen Spiegel spiegeln? Hier siehst du zwei Möglichkeiten, wie das geht.
So ein Klecksbild kannst du ganz einfach zu Hause nachmachen. Um es herzustellen, brauchst du ein Blatt Papier und Tinte.
1.Schritt: Falte das Blatt Papier in der Mitte zusammen und dann wieder auf.
2.Schritt: Nun gibst du einige Tropfen Tinte auf die eine Hälfte des Blattes.
3.Schritt: Jetzt musst du das Blatt wieder zusammenfalten und glatt streichen.
4.Schritt: Wenn du das Blatt wieder auffaltest, siehst du dein Klecksbild.
5.Schritt: Die Faltlinie in der Mitte des Blattes kannst du farbig kennzeichnen.Auch dieses Verfahren kannst du leicht ausprobieren. Dazu benötigst du wieder ein Blatt Papier und eine Stecknadel.
1.Schritt: Als erstes musst du das Blatt wieder in der Mitte falten und anschließend öffnen.
2.Schritt: Nun zeichnest du ein beliebiges Dreieck auf die eine Hälfte des Blattes.
3. Schritt: Jetzt faltest du das Blatt wieder zusammen. Dabei muss das Dreieck jedoch nach außen (zu dir) zeigen.
4.Schritt: Als nächstes stichst du mit Hilfe der Nadel durch die Eckpunkte des Dreiecks und entlang der Linien.
5.Schritt: Wenn du das Blatt wieder öffnest, siehst du auf der zweiten Hälfte des Blattes das Abbild deines Dreiecks.
6.Schritt: Als letztes kannst du die Mittellinie wieder farbig kennzeichnen und die durchstochenen Punkte mit einem Stift verbinden.Mit diesen beiden Verfahren kannst du mit wenigen Werkzeugen ein Spiegelbild erzeugen.
Ordne die Begriffe den Lücken zu. Ziehe dabei mit der linken Maustaste an ihnen und lasse sie fallen, wenn die Lücke rot wird.
Das Dreieck, von dem du beim Durchstechen ausgehst, heißt Urfigur. Das Dreieck, das beim Spiegeln entsteht, wird als Bildfigur bezeichnet. Urfigur und Bildfigur sind symmetrisch zueinander. Legt man die beiden Dreiecke übereinander, dann überdecken sie sich vollständig, d.h. sie sind deckungsgleich. Die Faltlinie heißt Spiegelachse. Das Verfahren, durch das die Bildfigur ensteht, nennt man Abbildung. Dabei wird jedem Urpunkt genau ein Bildpunkt zugeordnet.
Wichtige Begriffe
- Die Ausgangsfigur bei einer Abbildung heißt Urfigur oder Originalfigur.
- Die entstandene Figur nennt man Bildfigur.
- Urfigur und Bildfigur sind deckungsgleich zueinander. Ein anderes Wort für deckungsgleich ist kongruent.
- Bei einer Abbildung wird jedem Urpunkt genau ein Bildpunkt zugeordnet.
- Die Gerade, an der gespiegelt wird, heißt Spiegelachse oder Symmetrieachse.
Ordne die Wörter den richtigen Lücken zu!
Mein Name ist spiegelverkehrt zum blauen Original. Das heißt die Buchstaben sind in umgekehrter Reihenfolge angeordnet. Bei der Spiegelung hat sich also der Orientierungssinn geändert. Mein gespiegelter Name ist daher gegensinnig kongruent.
Es gibt aber nicht nur Unterschiede zu meinem Originalnamen. Versuche die verschüttelten Buchstaben richtig zu ordnen und die Wörter richtig zu entschlüsseln! Schreibe das richtige Wort in die Lücke.
Die Buchstaben haben trotzdem dieselbe Höhe und eine unveränderte Breite. Außerdem besitzen sie immer noch die gleiche Form.
Eine Abbildung, bei der die Urfigur an einer Spiegelachse gespiegelt wird, heißt Achsenspiegelung
Sieh dir das Urbild und das Spiegelbild des Männchens genau an. Achte dabei auf die Abstände der Urpunkte zur Spiegelachse. Vergleiche sie dann mit den Abständen der Bildpunkte zur Spiegelachse. Was fällt dir dabei auf?
Betrachte dann auch die Strecke zwischen einem Urpunkt und dessen Bildpunkt. Wie verhält sich diese Strecke zur Spiegelachse?
Wir wollen nochmal zusammenfassen, was wir bis jetzt gelernt haben.
Achsenspiegelung
- Die Achsenspiegelung ist eine Abbildung, bei der jedem Urpunkt genau ein Bildpunkt zugeordnet wird.
- Dabei wird ein Urpunkt z.B. mit A, B, C,... bezeichnet, ein Bildpunkt mit A', B', C',...(Lies: A Strich).
- Der Urpunkt und der Bildpunkt sind gleich weit von der Spiegelachse entfernt, d.h. die Spiegelachse halbiert die Strecke zwischen Urpunkt und Bildpunkt.
- Die Spiegelachse ist eine Gerade und wird meist mit einem Kleinbuchstaben, z.B. a, versehen.
- Bei einer Achsenspiegelung ist die Verbindungsstrecke zwischen Ur- und Bildpunk immer senkrecht zur Spiegelachse.
- Außerdem ändert sich bei der Achsenspiegelung der Orientierungssinn der Urfigur, d.h. Urfigur und Bildfigur sind gegensinnig kongruent.
2.Station: Achsenspiegelung durch Konstruktion
Natürlich kannst du eine Achsenspiegelung nicht nur über Klecksbilder oder mit Hilfe einer Nadel erzeugen. Viel einfacher lässt sich eine Achsenspiegelung mit Hilfe des Geodreiecks konstruieren.
Die Konstruktion der Achsenspiegelung wird noch genauer, wenn du sie mit einem Geodreieck und einem Zirkel durchführst.
Hier kannst du die Schritte einer Achsenspiegelung nochmal selbst nachvollziehen. Dafür musst du die Kästchen nacheinander anklicken. Wenn du in der rechten oberen Ecke auf die Pfeile drückst, kannst du von neuem beginnen. Viel Spass beim Ausprobieren!


3.Station:Übungen
Wende jetzt dein Wissen über die Achsenspiegelung auf die folgende Aufgabe an. Kreuze jeweils Richtig oder Falsch an.
Du siehst hier das Bild eines Krankenwagens. Die Schrift ist mit Absicht so auf den Krankenwagen geklebt worden. Kannst du dir denken, warum die Aufschrift "Rettungsdienst" spiegelverkehrt ist?
Wer ganz besonders schnell war, darf sich jetzt belohnen. Hier findest du den Link zu einem Spiel, bei dem es um die Achsenspiegelung geht. Du siehst Landschaften, die in der Mitte geteilt sind. Auf der rechten Seite sind jeweils ein paar Fehler im Vordergrund eingebaut. Also musst du diese Seite anpassen. Dabei steigert sich jedesmal die Anzahl der Fehler. Du hast aber immer nur wenige Sekunden Zeit, um die Fehler zu finden. Daher musst du schnell sein. Viel Spaß beim Spielen!
Storybook