Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Funktion - eine eindeutige Zuordnung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{Lernpfad-Navigation| | |||
Im Rahmen dieses Lernpfades | |||
#[[Einführung von Funktionen]] | |||
#[[Funktion - eine eindeutige Zuordnung]] | |||
#[[Sprache der Funktionen]] | |||
}} | |||
Im Rahmen dieses Lernpfades solltest du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben. | |||
{{Lösung versteckt|Den Funktionsbegriff kennen und verstehen können. |Lernziele |Lernziele}} | {{Lösung versteckt|Den Funktionsbegriff kennen und verstehen können. |Lernziele |Lernziele}} | ||
| Zeile 39: | Zeile 46: | ||
{{LearningApp|app=ppvafpsdn20|width=100%|height=400px}} | {{LearningApp|app=ppvafpsdn20|width=100%|height=400px}} | ||
{{ | {{Fortsetzung|weiter=Sprache der Funkionen|weiterlink=Sprache der Funktionen|vorher=zurück|vorherlink=Einführung in die Funktionen}} | ||
| | |||
| | |||
| | |||
}} | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Analysis]] | |||
Aktuelle Version vom 24. April 2022, 10:17 Uhr
Lernpfad
Funktion - eine eindeutige Zuordnung
Im Rahmen dieses Lernpfades solltest du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben.
Den Funktionsbegriff kennen und verstehen können.
- FA 1.1: Für gegebene Zusammenhänge entscheiden können, ob man sie als Funktion betrachten kann.
Funktionen
Funktionen sind Zuordnungen mit einer besonderen Eigenschaft: Als Funktion bezeichnet man eine Zuordnung, die jedem Argument genau einen Wert, den Funktionswert, zuordnet. Vereinfacht gesagt: "Eine Funktion ist eine eindeutige Zuordnung."
Musterbeispiel
Lösung
- Da jeder Mensch (Argument) nur eine leibliche Mutter (Wert) besitzt, handelt es sich bei dieser Zuordnung um eine eindeutige Zuordnung, also um eine Funktion.
- Da eine Mutter (Argument) mehrere Kinder (Wert) haben kann, handelt es sich bei dieser Zuordnung um keine eindeutige Zuordnung, also um keine Funktion.
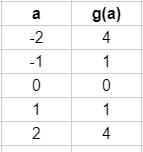
- Da jedem Argument a genau ein Wert g(a) zugeordnet ist, handelt es sich um die Wertetabelle einer Funktion.
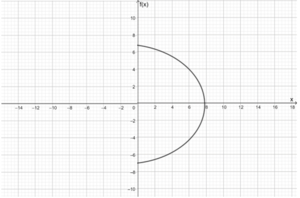
- Da einigen Argumenten mehrere Werte zugeordnet werden, handelt es sich nicht um einen Funktionsgraphen.
Üben
Lösung
- Ja, da es sich um eine eindeutige Zuordnung zwischen jedem Auto (Argument) und seinem Kennzeichen (Wert) handelt.
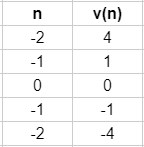
- Nein, da einige Argumente (beispielsweise -2) zwei Werte zugeordnet werden, handelt es sich um keine Wertetabelle einer Funktion.
- Ja, da es sich um eine eindeutige Zuordnung zwischen jedem erwachsenen Österreicher (Argument) und seiner Sozialversicherungsnummer (Wert) handelt.
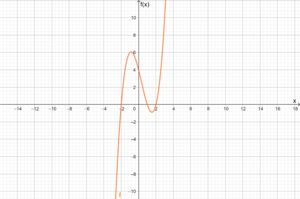
- Ja, da jedem Argument genau ein Wert zugeordnet wird, handelt es sich um den Graphen einer Funktion (Funktionsgraph).
Siehe auch
- Vorlage:Show-Hide (in englischer Sprache)