Eigenschaften der Achsenspiegelung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
 
(13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 2: Zeile 2:
__NOCACHE__
__NOCACHE__
{{Box|1= Lernpfad Eigenschaften der Achsenspiegelung|2=  
{{Box|1= Lernpfad Eigenschaften der Achsenspiegelung|2=  
[[Bild:Spiegel7.jpg|300px|right]]


*'''Zeitbedarf''': 45 Min.
*'''Zeitbedarf''': 45 Min.
*'''Material''': dein Heft, Stifte und ein Geodreieck
*'''Material''': dein Heft, Stifte und ein Geodreieck


'''Im Teil 1 der Lernpfadgruppe hast du ja schon einige grundlegende Dinge über das Thema Achsenspiegelung gelernt. Im zweiten Teil soll es jetzt um die Eigenschaften der Achsenspiegelung gehen.'''
Im Teil 1 der Lernpfadgruppe hast du schon einige grundlegende Dinge über das Thema Achsenspiegelung gelernt. Im zweiten Teil soll es jetzt um die Eigenschaften der Achsenspiegelung gehen.
 
Schreibe dir wieder alle Merksätze in dein Heft!


'''Schreibe dir wieder alle Merksätze in dein Heft!'''


[[Datei:Logo Mathematik-digital 2011.png|200px|left|verweis=Mathematik-digital]]
[[Datei:Logo Mathematik-digital 2011.png|200px|left|verweis=Mathematik-digital]]
Zeile 22: Zeile 24:
{{Box|1=Urpunkt und Bildpunkt|2=
{{Box|1=Urpunkt und Bildpunkt|2=
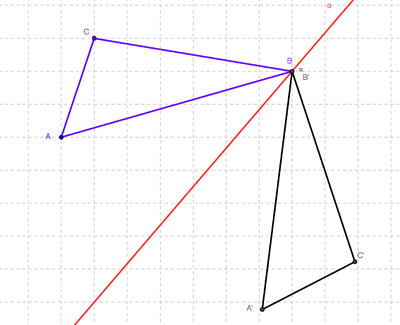
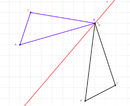
Du siehst hier eine Achsenspiegelung bei der ein Punkt des Urdreiecks auf der Spiegelachse liegt. Das heißt Urpunkt und Bildpunkt sind gleich, B=B'.
Du siehst hier eine Achsenspiegelung bei der ein Punkt des Urdreiecks auf der Spiegelachse liegt. Das heißt Urpunkt und Bildpunkt sind gleich, B=B'.
[[Bild:Fixpunkt.png|500px|center]]
[[Bild:Fixpunkt.png|400px|center]]
 
<div class="schuettel-quiz">
<div class="schuettel-quiz">


Zeile 38: Zeile 41:
{{Box|1=Fixpunkt und Fixpunktgerade|2=
{{Box|1=Fixpunkt und Fixpunktgerade|2=


* Ein Punkt, der sich genau auf der Spiegelachse befindet, heißt '''Fixpunkt'''. [[Bild:Spiegel2.jpg|300px|right]]
[[Bild:Spiegel_Achsensp.jpg|300px|right]]
* Ein Punkt, der sich genau auf der Spiegelachse befindet, heißt '''Fixpunkt'''.  
* Jeder Fixpunkt wird auf sich selbst abgebildet, somit sind in diesem Fall Urpunkt und Bildpunkt gleich.
* Jeder Fixpunkt wird auf sich selbst abgebildet, somit sind in diesem Fall Urpunkt und Bildpunkt gleich.
* Die Spiegelachse besteht ausschließlich aus Fixpunkten.
* Die Spiegelachse besteht ausschließlich aus Fixpunkten.
Zeile 51: Zeile 55:
Vielleicht helfen dir die folgenden Applets die Eigenschaften herauszufinden.  
Vielleicht helfen dir die folgenden Applets die Eigenschaften herauszufinden.  


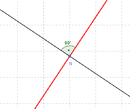
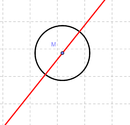
===Kreistreue===
===Kreistreue und Geradentreue===
Ziehe am Mittelpunkt M!
<div class="grid">
<ggb_applet height="400" width="400" showResetIcon="true" id="n78nymrx" /> <br>  
<div class="width-1-2">
Ziehe am Mittelpunkt M! <br /><br>
<ggb_applet height="400" width="400" showreseticon="true" id="n78nymrx" /> <br> </div>
<div class="width-1-2">Bewege die Gerade g! <br /><br>
<ggb_applet height="400" width="400" showreseticon="true" id="whmjm2ds" /> <br></div>
</div>


===Geradentreue===
Bewege die Gerade g!
<ggb_applet height="400" width="400" showResetIcon="true" id="whmjm2ds" /> <br>


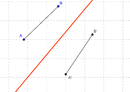
===Längentreue===
===Längentreue und Winkeltreue===
Ziehe am Punkt B!
<ggb_applet height="400" width="400" showResetIcon="true" id="qqccuqf4" /> <br>


<ggb_applet width="634" height="519" version="3.2" ggbBase64="UEsDBBQACAAIAMmGcz4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnNcts2ED43T8HhoTfRBEjK0lRKRnbSjGeceKZKc+gNIlcSaopkCdCW/VbJg+SZuvihTP1GipXEsS4UF8Bi8X27iwXYezWfpc4NlILnWd8lnu86kMV5wrNJ363kuNVxX7180ZtAPoFRyZxxXs6Y7LuBR10lr/jLF7/1xDS/dViqu3zkcNt3xywV4DqiKIElYgogl+SsmvOUs/LuavQvxFI8NBglF1lR4SyyrFAWz5JLLurXEz1hkXL5mt/wBEonzeO+247QdPz3EUrJY5b23dA3Etp36UojigLVOs1Lfp9nUnV/UD5GieMIfg+ICFWy3oleaA+qOOUJZ5lajLYDOznOLU/kFE0IQlQJfDJFWyNyarTFeV4mwzshYebM/4EyR3NIpIC+M2+BeRNoF04Y+bqp+abVwM0QpERahMPm8ADYpORJDZT6fyHO8jRZNBc5z+Q5K2RVakoDKxrKO6UfpyqVvYNskoKVUUR8CvH1KJ8PDQaBUf3hrtBDtD2jyXme5qVTKnQj7GCfI/PUfZShi16+7uPrHlaHUrpoJ12qe+jnyDx1r5RnxjS7cFIvmvj1NFw4SqBQRE9cLD5lI0BmXafKuLysX9ADru1SiRnwvpqNMASaPrDQSY6ls3ey4j29aygzSI2PZEhtlVfCuVG+aObShiQQ8xm+mgYLCVN0/Y0GGGkCkxJqw00AGcB0q9/0wxVx76Q2Qtkg0NZYYibA9Ui1lkE8FZCJgsME0iqb3PLsGlIVvhJDp++iS3HqE1xywiT2VykBUpgBBpDU3qKdbYHawF1ki1wHfu25tv0Bf2ze6Dnax1haTBlK6thI2R2mgeZitb53ebIMAcsQSr0+jMZCKVBkFQCJTX3SerhToEodLw0mNIDCmatxnQ7GaN9tES9su869Ga57mehSaUHPHFjqDShfgWf4Q+G5Go8FSLWeFqV6OST4Eei1qNfW0/negdjF+WzGssTJ2AwnGsJEyTVmXO0XDvOVizmMKCgNTpWsG5jRZnWsMSGsthpr5i7nHjnFEM9ACJ0gZTMVPoYw/1voIl2NX0B20bUEuG8QbwVe2NGY4z/a7qwm2B2LhP8y00eYNMdnuAXHXC5wThXlF5nEpAc6iaznsmuAQm0iV9mHkmVC1RKmTyNH7hUoZ88lj/iallA9jx0IQxMIZ2uBMDosEEZPOBCCU+PWtLtnJKD/6xHUpp4W8VHyhKNgmWldpm1LeA6jm+j+8mk337qWWBCFvdV4tKeyIOIWF9EwoH7gn3ZocBp2HkM28dfpJnvSTSPDdriRbHIAjayMG9FVC9M0v/0LxinMNc7flprO11PTcuX4i+QmqsYh2pF3esQK5/XzQYfWO2pEj4fPn88En9Dr2IrDxzrjePi8+Ro+DWueNEBYktE6vsLj4fP22eGjC9XHVEeXuCGsbJlvzJb5dm2vjHdvlWpvWSAZb6+Lwr3roi101Dcqh5ZGO0qfrq01fVtrtkjHI7sOAKuL2FX6bEf/HS/LvFzB/8zgH6/hf/Y7K3Lxx24WVo4CdshPPRA0E58fdJu/YxT4G0EcbANxcDiIg6cFYuCR9uJ+JVqC8/ToOA634Tg8HMfh08Kx7bVDv/Ej9bWLv/SLvsPh0wJhjqAPQC4BnBx2EE2OcRDdY/87SrrFbWs5D3Tt4YWuoE/M7k9DjwTtX+ckugftgy20w2G0w69Eu7ppW42t+t5tSR7aTZh4UddvBOnaN4+n6wKbLiPOmg7w4A10uzd8+bRPml29pGjk2V1XFe0NfrH/eeoxdxWtdtcyv9FxDqH5kZcV34W0zwfR9fmbiPohd0qtyPJEfzZPJ80PcPqTs/3m/vJ/UEsHCH6oAwlhBQAApR8AAFBLAQIUABQACAAIAMmGcz5+qAMJYQUAAKUfAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAmwUAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
Ziehe am Punkt B! <br><br>
<ggb_applet height="450" width="600" showreseticon="true" id="grmevj6j" /> <br>


<br>
Ziehe am Punkt B! <br><br>
<ggb_applet height="400" width="400" showreseticon="true" id="qqccuqf4" /> <br>  


{{Box|1=Treue|2=
{{Box|1=Treue|2=
Zeile 80: Zeile 86:


{{Box|1=Eigenschaften der Achsenspiegelung|2=
{{Box|1=Eigenschaften der Achsenspiegelung|2=
* '''Geradentreue''': Jede Gerade wird wieder auf eine Gerade abgebildet. [[Bild:Spiegel2.jpg|300px|right]]
[[Bild:Spiegel_Achsensp.jpg|300px|right]]
 
* '''Geradentreue''': Jede Gerade wird wieder auf eine Gerade abgebildet.  
* '''Kreistreue''': Die Bildfigur eines Kreises ist ebenfalls ein Kreis. Dabei bleibt der Radius bei der Spiegelung unverändert.
* '''Kreistreue''': Die Bildfigur eines Kreises ist ebenfalls ein Kreis. Dabei bleibt der Radius bei der Spiegelung unverändert.
* '''Längentreue''': Eine Strecke wird wieder auf eine Strecke abgebildet und besitzt die gleiche Länge wie das Original.
* '''Längentreue''': Eine Strecke wird wieder auf eine Strecke abgebildet und besitzt die gleiche Länge wie das Original.
Zeile 100: Zeile 108:
</div>
</div>
|3=Übung}}
|3=Übung}}




Zeile 117: Zeile 124:
'''Mit Hilfe der folgenden Applets kannst du entdecken, worum es bei den zwei Sonderfällen geht.'''
'''Mit Hilfe der folgenden Applets kannst du entdecken, worum es bei den zwei Sonderfällen geht.'''


Ziehe am Mittelpunkt M!  
<div class="grid">
<ggb_applet height="400" width="400" showResetIcon="true" id="pggppcnf" /> <br>  
<div class="width-1-2">
Ziehe am Mittelpunkt M! <br><br>
<ggb_applet height="400" width="400" showreseticon="true" id="pggppcnf" /> <br> </div>
<div class="width-1-2">
Bewege den Punkt N!  <br><br>
<ggb_applet height="400" width="400" showreseticon="true" id="pyagkrxk" /> <br> </div>
</div>
 
 


Bewege den Punkt N!
<ggb_applet height="400" width="400" showResetIcon="true" id="pyagkrxk" /> <br>


{{Box|1=Fixkreis und Fixgerade|2=
{{Box|1=Fixkreis und Fixgerade|2=
Zeile 144: Zeile 157:
'''Jetzt wollen wir mal sehen, was du alles gelernt hast! Kannst du dein Wissen in den folgenden Aufgaben anwenden?'''
'''Jetzt wollen wir mal sehen, was du alles gelernt hast! Kannst du dein Wissen in den folgenden Aufgaben anwenden?'''


{{Box|1=Meomory-Quiz|2=
{{Box|1=Memory-Quiz|2=
<div class="memo-quiz">
<div class="memo-quiz">


Zeile 158: Zeile 171:
{{!}} [[Bild:Fixkreis.png|130px]] {{!}}{{!}} Fixkreis
{{!}} [[Bild:Fixkreis.png|130px]] {{!}}{{!}} Fixkreis
{{!}}-
{{!}}-
{{!}} [[Bild:Kreis1.png|130px]] {{!}}{{!}} Kreistreue
{{!}} [[Bild:Kreis_22.png|130px]] {{!}}{{!}} Kreistreue
{{!}}-
{{!}}-
{{!}} [[Bild:StreckeAB.png|130px]] {{!}}{{!}} Längentreue
{{!}} [[Bild:StreckeAB.png|130px]] {{!}}{{!}} Längentreue
{{!}}-
{{!}}-
{{!}} [[Bild:Parallele.png|130px]] {{!}}{{!}} Parallelentreue
{{!}} [[Bild:Parallele_22.png|130px]] {{!}}{{!}} Parallelentreue
{{!}}-
{{!}}-
{{!}} [[Bild:Winkel.png|130px]] {{!}}{{!}} Winkeltreue
{{!}} [[Bild:Winkel_Achsen.png|130px]] {{!}}{{!}} Winkeltreue
{{!}}}
{{!}}}


Zeile 175: Zeile 188:


Ordne die Begriffe dem richtigen Oberbegriff zu. Ziehe mit der linken Maustaste an den Begriffen und lasse sie fallen, wenn der Hintergrund rot wird.
Ordne die Begriffe dem richtigen Oberbegriff zu. Ziehe mit der linken Maustaste an den Begriffen und lasse sie fallen, wenn der Hintergrund rot wird.
{|
{{{!}}
| Fixelemente der Achsenspiegelung || Fixpunkt || Fixgerade || Fixkreis || Fixpunktgerade  
{{!}} Fixelemente der Achsenspiegelung {{!}}{{!}} Fixpunkt {{!}}{{!}} Fixgerade {{!}}{{!}} Fixkreis {{!}}{{!}} Fixpunktgerade  
|-
{{!}}-
| Eigenschaften der Achsenspiegelung || Längentreue || Winkeltreue || Kreistreue || Parallelentreue || Geradentreue
{{!}} Eigenschaften der Achsenspiegelung {{!}}{{!}} Längentreue {{!}}{{!}} Winkeltreue {{!}}{{!}} Kreistreue {{!}}{{!}} Parallelentreue {{!}}{{!}} Geradentreue
|-
{{!}}-
| Wörter mit gleicher Bedeutung || kongruent || deckungsgleich  
{{!}} Wörter mit gleicher Bedeutung {{!}}{{!}} kongruent {{!}}{{!}} deckungsgleich  
|-
{{!}}-
| Zur Abbildung gehörende Elemente || Urpunkt ||Spiegelachse || Bildpunkt || Urfigur ||Bildfigur
{{!}} Zur Abbildung gehörende Elemente {{!}}{{!}} Urpunkt {{!}}{{!}} Spiegelachse {{!}} Bildpunkt {{!}}{{!}} Urfigur {{!}}{{!}} Bildfigur
|}
{{!}}}
</div>
</div>
|3=Übung}}
|3=Übung}}
Zeile 203: Zeile 216:
[[Kategorie:Mathematik-digital]]
[[Kategorie:Mathematik-digital]]
[[Kategorie:Sekundarstufe_1]]
[[Kategorie:Sekundarstufe_1]]
[[Kategorie:Achsenspiegelung]]
[[Kategorie:Lernpfad]]
[[Kategorie:Lernpfad]]
[[Kategorie:ZUM2Edutags]]
[[Kategorie:Mathematik]]
[[Kategorie:Mathematik]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:R-Quiz]]
[[Kategorie:Geometrie]]
[[Kategorie:GeoGebra]]

Aktuelle Version vom 24. April 2022, 10:08 Uhr


Lernpfad Eigenschaften der Achsenspiegelung
Spiegel7.jpg
  • Zeitbedarf: 45 Min.
  • Material: dein Heft, Stifte und ein Geodreieck

Im Teil 1 der Lernpfadgruppe hast du schon einige grundlegende Dinge über das Thema Achsenspiegelung gelernt. Im zweiten Teil soll es jetzt um die Eigenschaften der Achsenspiegelung gehen.

Schreibe dir wieder alle Merksätze in dein Heft!


Logo Mathematik-digital 2011.png
Lernpfadgruppe Mathematik-digital.de


Spiegel7.jpg


1.Station: Besondere Punkte und Geraden

Urpunkt und Bildpunkt

Du siehst hier eine Achsenspiegelung bei der ein Punkt des Urdreiecks auf der Spiegelachse liegt. Das heißt Urpunkt und Bildpunkt sind gleich, B=B'.

Fixpunkt.png

Finde die unverdrehte Lösung zu den verdrehten Wörtern! Achte dabei auch auf die richtige Schreibweise.

Liegt ein Punkt bei einer Achsenspiegelung genau auf der Spiegelachse, nennt man einen solchen Punkt Fixpunkt.

Dabei wird jeder Fixpunkt auf sich selbst abgebildet. Alle Punkte auf der Spiegelachse sind Fixpunkte.

Daher ist die Spiegelachse eine Fixpunktgerade.

Fixpunkt und Fixpunktgerade
Spiegel Achsensp.jpg
  • Ein Punkt, der sich genau auf der Spiegelachse befindet, heißt Fixpunkt.
  • Jeder Fixpunkt wird auf sich selbst abgebildet, somit sind in diesem Fall Urpunkt und Bildpunkt gleich.
  • Die Spiegelachse besteht ausschließlich aus Fixpunkten.
  • Daher nennt man die Spiegelachse auch Fixpunktgerade.


2.Station: Wichtige Eigenschaften der Achsenspiegelung

Jetzt wollen wir uns die besonderen Eigenschaften der Achsenspiegelung anschauen. Es gibt fünf Eigenschaften, die du kennen solltest, um eine Achsenspiegelung richtig ausführen zu können! Also los geht´s!

Vielleicht helfen dir die folgenden Applets die Eigenschaften herauszufinden.

Kreistreue und Geradentreue

Ziehe am Mittelpunkt M!

GeoGebra

Bewege die Gerade g!

GeoGebra


Längentreue und Winkeltreue

Ziehe am Punkt B!

GeoGebra


Ziehe am Punkt B!

GeoGebra


Treue

Versuche die Wörter richtig zuzuordnen. Du musst dabei wieder mit der linken Maustaste an den Wörtern ziehen und sie fallen lassen, wenn die Lücke rot wird.

Eine Gerade wird bei einer Achsenspiegelung wieder auf eine Gerade abgebildet, d.h. die Achsenspiegelung ist geradentreu. Auch das Spiegelbild eines Kreises ist ein Kreis, somit ist die Achsenspiegelung auch kreistreu. Alle Strecken werden auf Strecken der gleichen Länge abgebildet. Die Achsenspiegelung ist daher längentreu. Ähnlich verhält es sich bei der Abbildung von Winkeln. Ein Winkel wird wieder auf einen Winkel mit unverändertem Maß abgebildet. Man nennt die Achsenspiegelung daher auch winkeltreu. Die letzte Eigenschaft bezieht sich auf parallele Geraden. Denn bei einer Achsenspiegelung ist das Bild einer Parallele zur Spiegelachse auch eine parallele Gerade. Das heißt die Achsenspiegelung ist auch parallelentreu.

Jetzt kennst du also alle Eigenschaften der Achsenspiegelung! Du findest sie auch nochmal in einem Merksatz.

Eigenschaften der Achsenspiegelung
Spiegel Achsensp.jpg
  • Geradentreue: Jede Gerade wird wieder auf eine Gerade abgebildet.
  • Kreistreue: Die Bildfigur eines Kreises ist ebenfalls ein Kreis. Dabei bleibt der Radius bei der Spiegelung unverändert.
  • Längentreue: Eine Strecke wird wieder auf eine Strecke abgebildet und besitzt die gleiche Länge wie das Original.
  • Winkeltreue: Ein Winkel wird auch auf einen Winkel abgebildet und behält dabei das gleiche Maß. Jedoch ist der Winkel danach entgegengesetzt orientiert.
  • Parallelentreue: Eine zur Spiegelachse parallele Gerade wird auf eine Parallele abgebildet.

Eigenschaften der Achsenspiegelung

Mal sehen, was du gelernt hast. Beantworte folgende Fragen zu den Eigenschaften der Achsenspiegelung. Es können auch mehrere Antworten richtig sein.

Eine Strecke mit 5cm wird durch eine Achsenspiegelung abgebildet. Wie lang ist sie nach der Spiegelung? (!6cm) (5cm) (!4cm)

Eine Achenspiegelung ist ... (!rechteckstreu) (parallelentreu) (!diagonalentreu) (kreistreu)

Eine Parallele zur Spiegelachse wird auf eine ... abgebildet. (!Diagonale) (!Senkrechte) (Parallele)


Finde die Fehler

Finde heraus, welche der Eigenschaften in diesem Bild bei der Spiegelung nicht eingehalten wurden! Wie viele Fehler entdeckst du?

Blumen.png

Hier geht`s zur Lösung!

Blumen1.png
Spiegel8.jpg

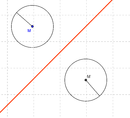
Sonderfälle der Achsenspiegelung

Mit Hilfe der folgenden Applets kannst du entdecken, worum es bei den zwei Sonderfällen geht.

Ziehe am Mittelpunkt M!

GeoGebra

Bewege den Punkt N!

GeoGebra



Fixkreis und Fixgerade

Finde die unverdrehte Lösung zu den verdrehten Wörtern! Achte auf Rechtschreibfehler!

Liegt der Mittelpunkt eines Kreises auf der Spiegelachse, so wird er auf sich selbst abgebildet.

Daher nennt man ihn Fixkreis. Steht eine Gerade senkrecht auf der Spiegelachse, wird sie bei einer Achsenspiegelung auf

sich selbst abgebildet. Sie heißt daher Fixgerade.

Das war die letzte Aufgabe für diese Station. Bestimmt konntest du sie lösen. Super!


3.Station: Übungen

Jetzt wollen wir mal sehen, was du alles gelernt hast! Kannst du dein Wissen in den folgenden Aufgaben anwenden?

Memory-Quiz

Achsenspiegelung
Finde die Paare aus je einem Bild und dem dazu passenden Begriff.

Fixpunkt.png Fixpunkt
Fixgerade.png Fixgerade
Fixkreis.png Fixkreis
Kreis 22.png Kreistreue
StreckeAB.png Längentreue
Parallele 22.png Parallelentreue
Winkel Achsen.png Winkeltreue


Dem Oberbegriff zuordnen

Ordne die Begriffe dem richtigen Oberbegriff zu. Ziehe mit der linken Maustaste an den Begriffen und lasse sie fallen, wenn der Hintergrund rot wird.

Fixelemente der Achsenspiegelung Fixpunkt Fixgerade Fixkreis Fixpunktgerade
Eigenschaften der Achsenspiegelung Längentreue Winkeltreue Kreistreue Parallelentreue Geradentreue
Wörter mit gleicher Bedeutung kongruent deckungsgleich
Zur Abbildung gehörende Elemente Urpunkt Bildpunkt Urfigur Bildfigur

Ich denke, du kennst jetzt alle wichtigen Begriffe der Achsenspiegelung!

Zusatzaufgabe

Welche der Geraden auf dem Bild ist die Spiegelachse?

Geraden LauraKlaus.png
Man erkennt schnell durch hinsehen, dass Gerade g4 die Spiegelachse sein muss. Die Geraden g2 ung g7 verlaufen parallel zur Spiegelachse. Die Geraden g3 und g5, sowie g1 und g6 schneiden die Spiegelachse jeweils in einem Fixpunkt.


Spiegel10.jpg
Achsensymmetrische Vierecke und Dreiecke
Abgerufen von „https://unterrichten.zum.de/index.php?title=Eigenschaften_der_Achsenspiegelung&oldid=125086“