Integralrechnung/Vorüberlegungen: Unterschied zwischen den Versionen
Main>Dickesen (Die Seite wurde neu angelegt: „Auf der ersten Seite hast Du gelernt, dass der zurückgelegte Weg in einem Diagramm, in dem die Geschwindigkeit gegen die Zeit aufgetragen ist, gleich dem Fläche…“) |
Keine Bearbeitungszusammenfassung |
||
| (79 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Auf der ersten Seite hast Du gelernt, dass der zurückgelegte Weg in einem Diagramm, in dem die Geschwindigkeit gegen die Zeit aufgetragen ist, gleich dem Flächeninhalt zwischen dem Graphen und der x-Achse ist. <br> | {{Navigation verstecken|{{Lernpfad Integral}}}} | ||
Aber wie kann man diesen Flächeninhalt denn nun genau bestimmen bzw. berechnen? | ==Vorüberlegungen: Vom Speziellen zum Allgemeinen== | ||
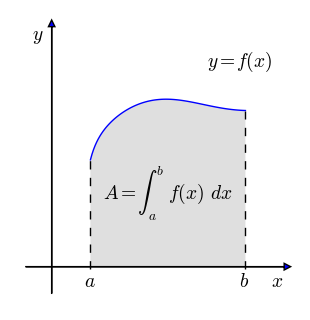
Auf der ersten Seite hast Du gelernt, dass der zurückgelegte Weg in einem Diagramm, in dem die Geschwindigkeit gegen die Zeit aufgetragen ist, gleich dem Flächeninhalt zwischen dem Graphen und der x-Achse ist. | |||
<br><br> | |||
{{Frage|Aber wie kann man diesen Flächeninhalt denn nun genau bestimmen bzw. berechnen?}} | |||
<br> | |||
<div align="center"> | |||
Dies ist die zentrale Frage des vorliegenden Lernpfades! | |||
</div> | |||
<br> | |||
Um einer Lösung näher zu kommen, fangen wir mit einfachen und sehr speziellen Graphen von Funktionen an und arbeiten uns ausgehend davon immer weiter hin zu schwierigeren und allgemeineren Graphen von Funktionen vor, damit wir am Ende eine Lösung für alle Eventualitäten in Händen halten! | |||
<br> | |||
{{Box|1=Aufgabe 2|2= | |||
Bestimme die Flächeninhalte zwischen den Graphen und der x-Achse innerhalb der angegebenen Grenzen in nachfolgenden Diagrammen. <br> | |||
Beschreibe dabei immer Deine Vorgehensweise! | |||
|3=Arbeitsmethode}} | |||
<br> | |||
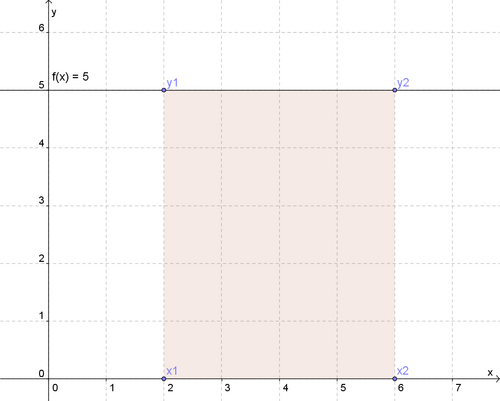
a) Konstante Funktion: <math>f(x)=5</math> in den Grenzen <math>x_1=2</math> und <math>x_2=6</math> | |||
<br><br> | |||
[[Bild:const_fkt.png|zentriert|500px]] | |||
<br> | |||
{{Lösung versteckt|1=Flächeninhalt: <math>A = 20.</math> <br> | |||
Die Fläche ist rechteckig, also berechnet sich der Flächeninhalt nach der Formel <math>A = </math> Breite <math>\cdot</math> Höhe. <br> | |||
Die Breite ist dabei durch die Grenzen <math>x_1</math> und <math>x_2</math> festgelegt, misst also | |||
<math>x_2 - x_1 = 6 - 2 = 4.</math> <br> | |||
Die Höhe ist durch den (konstanten) Funktionswert <math>f(x)=5</math> festgelegt. <br> | |||
Also: <math>A=4 \cdot 5 = 20.</math> | |||
}} | |||
<br> | |||
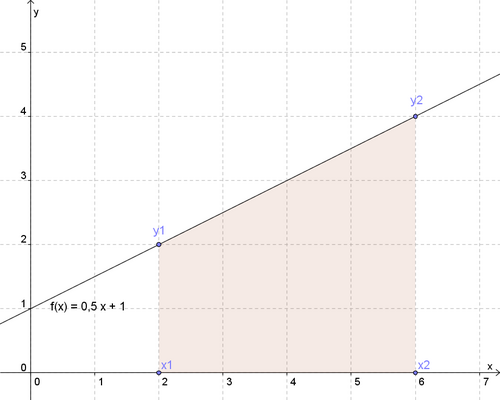
b) Lineare, nicht-konstante Funktion: <math>f(x)= 0,5 x + 1</math> in den Grenzen <math>x_1=2</math> und <math>x_2=6</math> | |||
<br><br> | |||
[[Bild:lin_fkt.png|zentriert|500px]] | |||
<br> | |||
{{Lösung versteckt|1=Flächeninhalt: <math>A = 12.</math> <br> | |||
Die Fläche lässt sich aufteilen in einen rechteckigen Teil ( Höhe <math> = y_1 = 2,</math> Breite <math> = x_2-x_1 = 4</math> ) mit <math>A=8</math> <br> | |||
und einen dreieckigen Teil ( Höhe <math> = y_2-y_1 = 2,</math> Grundseite <math> = x_2-x_1 = 4</math> ) mit <math>A=4</math>. <br> | |||
Also: <math>A = A_{\mathrm{Rechteck}} + A_{\mathrm{Dreieck}} = 8 + 4 = 12.</math> | |||
<br> | |||
'''Merke''' | |||
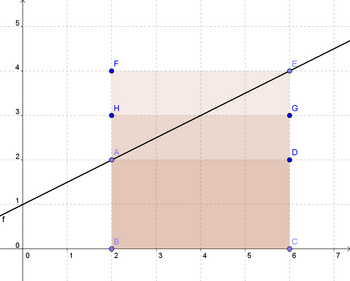
Allgemein berechnet sich eine solche aus Rechteck- und Dreieckfläche zusammengesetzte Fläche natürlich nach der Formel <math>A = a \cdot b + \frac{1}{2} \cdot h \cdot b</math>, wenn <math>a</math> die Höhe des Rechtecks, <math>h</math> die Höhe des Dreiecks und <math>b</math> die Breite des Dreiecks bzw. Rechtecks sind. <br> | |||
Diese Summe aus den beiden Einzelflächen kann nun interpretiert werden als der Mittelwert der unteren Rechteckfläche (Rechteck ABCD) und der oberen Rechteckfläche (Rechteck BCEF)! <br> | |||
Seine Fläche entspricht dem Rechteck BCGH. | |||
[[Bild:Flaeche_mittelwert.png|zentriert|350px]] | |||
}} | |||
<br> | |||
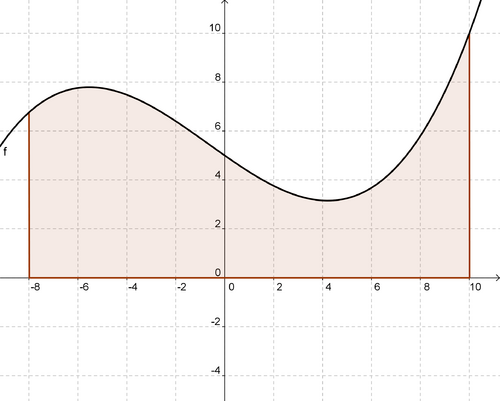
c) Ausgehend von den Aufgabenteilen a) und b) sollst Du hier nur eine Möglichkeit beschreiben, wie man die markierte Fläche zumindest näherungsweise bestimmen könnte. Dazu soll eine | |||
Funktion dritten Grades als Beispiel für eine Funktion im Allgemeinen dienen: <math>f(x) = \frac{1}{100} \cdot x^3 + \frac{1}{50} \cdot x^2 - \frac{7}{10} \cdot x + 5</math> in den Grenzen -8 und 10.<br> | |||
<br><br> | |||
[[Bild:flaeche_allgemein.png|zentriert|500px]] | |||
<br> | |||
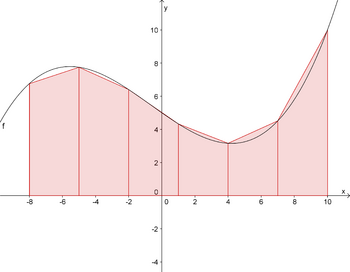
{{Lösung versteckt|1=Man könnte die Fläche unter dem Graphen von <math>f</math> in viele schmale Trapeze aufteilen, deren Fläche berechnen und die gesuchte Fläche durch die Summe der Trapezflächen (''Trapezsumme'') annähern. | |||
<br> | |||
Das Ganze sähe dann mit <math>n = 6</math> gleich breiten Trapezstreifen folgendermaßen aus: <br> | |||
[[Bild:flaeche_allgemein_summen.png|zentriert|350px]] | |||
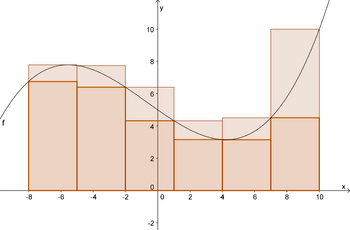
'''Merke''' | |||
Mathematisch sehr viel einfacher zu handhaben sind jedoch Rechteckflächen. Man unterscheidet ''Obersumme'' und ''Untersumme''. Die gesuchte Fläche liegt dann zwischen Ober- und Untersumme. | |||
<br> | |||
[[Bild:flaeche_summen.png|zentriert|350px]] | |||
}} | |||
{{Fortsetzung|weiter=Ober- und Untersumme|weiterlink=Integral/Ober- und Untersumme}} | |||
[[Kategorie:Integralrechnung]] | |||
Aktuelle Version vom 23. April 2022, 16:40 Uhr
Vorüberlegungen: Vom Speziellen zum Allgemeinen
Auf der ersten Seite hast Du gelernt, dass der zurückgelegte Weg in einem Diagramm, in dem die Geschwindigkeit gegen die Zeit aufgetragen ist, gleich dem Flächeninhalt zwischen dem Graphen und der x-Achse ist.
Dies ist die zentrale Frage des vorliegenden Lernpfades!
Um einer Lösung näher zu kommen, fangen wir mit einfachen und sehr speziellen Graphen von Funktionen an und arbeiten uns ausgehend davon immer weiter hin zu schwierigeren und allgemeineren Graphen von Funktionen vor, damit wir am Ende eine Lösung für alle Eventualitäten in Händen halten!
Bestimme die Flächeninhalte zwischen den Graphen und der x-Achse innerhalb der angegebenen Grenzen in nachfolgenden Diagrammen.
a) Konstante Funktion: in den Grenzen und
Flächeninhalt:
Die Fläche ist rechteckig, also berechnet sich der Flächeninhalt nach der Formel Breite Höhe.
Die Breite ist dabei durch die Grenzen und festgelegt, misst also
Die Höhe ist durch den (konstanten) Funktionswert festgelegt.
b) Lineare, nicht-konstante Funktion: in den Grenzen und
Flächeninhalt:
Die Fläche lässt sich aufteilen in einen rechteckigen Teil ( Höhe Breite ) mit
und einen dreieckigen Teil ( Höhe Grundseite ) mit .
Also:
Merke
Allgemein berechnet sich eine solche aus Rechteck- und Dreieckfläche zusammengesetzte Fläche natürlich nach der Formel , wenn die Höhe des Rechtecks, die Höhe des Dreiecks und die Breite des Dreiecks bzw. Rechtecks sind.
Diese Summe aus den beiden Einzelflächen kann nun interpretiert werden als der Mittelwert der unteren Rechteckfläche (Rechteck ABCD) und der oberen Rechteckfläche (Rechteck BCEF)!
Seine Fläche entspricht dem Rechteck BCGH.
c) Ausgehend von den Aufgabenteilen a) und b) sollst Du hier nur eine Möglichkeit beschreiben, wie man die markierte Fläche zumindest näherungsweise bestimmen könnte. Dazu soll eine
Funktion dritten Grades als Beispiel für eine Funktion im Allgemeinen dienen: in den Grenzen -8 und 10.
Man könnte die Fläche unter dem Graphen von in viele schmale Trapeze aufteilen, deren Fläche berechnen und die gesuchte Fläche durch die Summe der Trapezflächen (Trapezsumme) annähern.
Das Ganze sähe dann mit gleich breiten Trapezstreifen folgendermaßen aus:
Merke
Mathematisch sehr viel einfacher zu handhaben sind jedoch Rechteckflächen. Man unterscheidet Obersumme und Untersumme. Die gesuchte Fläche liegt dann zwischen Ober- und Untersumme.