Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Trigonometrische Funktionen/Einfluss von d: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
K (- ZUM2Edutags) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 6: | Zeile 6: | ||
Wir betrachten nun den Einfluss von <math> d </math> in | Wir betrachten nun den Einfluss von <math> d </math> in | ||
:<math> x \rightarrow \sin x + d </math>. | :<math> x \rightarrow \sin x + d </math>. | ||
{{Box|1=Aufgabe D1|2= | {{Box|1=Aufgabe D1|2= | ||
| Zeile 70: | Zeile 70: | ||
Nun betrachten wir den Einfluss von <math> d </math> in | Nun betrachten wir den Einfluss von <math> d </math> in | ||
:<math> x \rightarrow \cos x + d </math>. | :<math> x \rightarrow \cos x + d </math>. | ||
{{Box|1= Aufgabe D4|2= | {{Box|1= Aufgabe D4|2= | ||
| Zeile 88: | Zeile 88: | ||
{{Fortsetzung|weiter=Zurück zu Station 1: Einfluss der Parameter|weiterlink=Trigonometrische Funktionen/Einfluss der Parameter}} | {{Fortsetzung|weiter=Zurück zu Station 1: Einfluss der Parameter|weiterlink=Trigonometrische Funktionen/Einfluss der Parameter}} | ||
[[Kategorie:Interaktive Übung]] | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie:GeoGebra]] | [[Kategorie:GeoGebra]] | ||
Aktuelle Version vom 23. April 2022, 16:29 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss von d
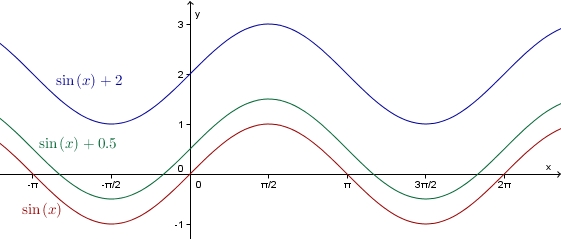
Wir betrachten nun den Einfluss von in
- .
Aufgabe D1

- Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von ändern.
- Stelle den Schieberegler auf ein. Wie ändert sich der Graph?
- Überlege dir, wie sich die Werte und sowie auf den Graphen auswirken und überprüfe deine Vermutung.
- Formuliere das Ergebnis deiner Untersuchungen.
Merek
Man erhält den Graph der Funktion
aus dem Graph der Sinusfunktion durch Verschiebung in Richtung der -Achse. Genauer:
- Ist positiv, so wird der Graph der Sinusfunktion um den Betrag von nach oben verschoben.
- Ist negativ, so wird der Graph der Sinusfunktion um den Betrag von nach unten verschoben.
Aufgabe D2
Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen!
Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig.
Eine mögliche Begründung:
Aufgabe D3
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen!
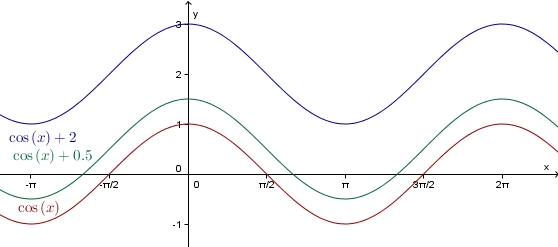
Nun betrachten wir den Einfluss von in
- .
Aufgabe D4

Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgabe D1 noch einmal .
Die allgemeine Kosinusfunktion verhält sich bei Variation von genauso wie die allgemeine Sinusfunktion.
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe D1 ein Hefteintrag "versteckt" ist!