Quadratische Funktionen erkunden/Übungen: Unterschied zwischen den Versionen
Main>Elena Jedtke (Übung "Modellieren" überarbeitet) |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (81 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Quadratische Funktionen erkunden}} | {{Navigation verstecken|{{Quadratische Funktionen erkunden}}|Lernschritte einblenden|Lernschritte ausblenden}} | ||
{{Box | |||
{{ | | | ||
|In diesem Kapitel des Lernpfads findest du Übungsaufgaben zu allen Inhalten, die du in den vorherigen Abschnitten kennengelernt hast. Sie sollen dir helfen, dein Wissen zu festigen. Klicke im Inhaltsverzeichnis einfach auf das Thema, zu dem du Übungsaufgaben bearbeiten möchtest. | |||
'''Hinweis:''' Du musst nicht alle Aufgaben dieser Seite bearbeiten. Suche dir gezielt Aufgaben zum Üben heraus. | |||
|Kurzinfo | |||
}} | |||
==Parameter== | |||
===Die Parameter der Scheitelpunktform=== | |||
{{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 17) [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
Zeichne die Graphen der folgenden Funktionen: | |||
'''a)''' <math>y=2 \cdot x^2</math> '''b)''' <math>y=0,5 \cdot x^2</math> '''c)''' <math>y=-x^2</math> | |||
'''d)''' <math>y=(x-2)^2</math> '''e)''' <math>y=(x+2)^2</math> '''f)''' <math>y=x^2+3</math> '''g)''' <math>y=x^2-3</math> | |||
{{Lösung versteckt|Schaue dir die Merksätze zu den Parametern <math>a, d</math> und <math>e</math> in deinem Hefter noch einmal an. Dadurch kannst du herausfinden wie die Parabel, die du zeichnen möchtest aussehen muss. | |||
Ermittle einzelne Punkte oder lege eine Wertetabelle an, um die Parabeln zu zeichnen.|Hilfe anzeigen|Hilfe verbergen}} | |||
{{Lösung versteckt|Gib für die Parameter <math>a, d</math> und <math>e</math> die Werte im Applet an, so dass g(x) einem der Funktionsterme (a)-(g) gleicht. Vergleiche zur Kontrolle die Parabel im Applet mit deiner gezeichneten Parabel. | |||
<ggb_applet id="cSvseGhd" width="700" height="500" /> | |||
|Lösung anzeigen|Lösung verbergen}}}} | |||
{{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 18) [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
In dieser Aufgabe werden die Parameter kombiniert, die du in dem Kapitel [[Mathematik-digital/Quadratische Funktionen erkunden/Die Parameter der Scheitelpunktform|Die Parameter der Scheitelpunktform]] kennengelernt hast. | |||
Gegeben ist die Wertetabelle: | Gegeben ist die Wertetabelle: | ||
[[Datei:Tabelle Übung1.PNG|rahmenlos | [[Datei:Tabelle Übung1.PNG|rahmenlos|750px|Übung zu Parametern]] | ||
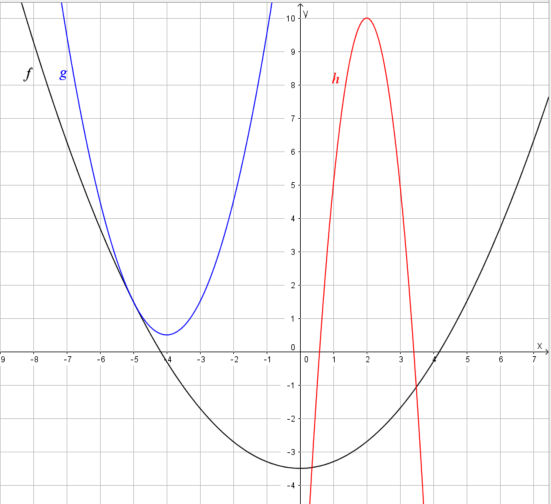
'''a)''' Zeichne die Graphen zu den Funktionen ''f''(x), ''g''(x) und ''h''(x) in das Koordinatensystem in deinem Hefter. Nicht alle y-Werte können sinnvoll in den Ausschnitt, der in dem Koordinatensystem gezeigt wird, eingetragen werden. | |||
{{Lösung versteckt|[[Datei:Lösung zu Übung1.PNG|rahmenlos|750px|Lösung zu Tabelle Übung1]]|Lösung anzeigen|Lösung verbergen}} | |||
''' | '''b)''' Bestimme die Funktionsterme in Scheitelpunktform. | ||
< | {{Lösung versteckt|1=Ist der Graph gestreckt, gestaucht und/oder gespiegelt? Durch die Beantwortung dieser Frage kannst du den Wert des Parameters <math>a</math> eingrenzen. Anschließend findest du den genauen Wert zum Beispiel durch systematisches Probieren und Abgleichen mit den gegebenen Funktionswerten in der Tabelle. | ||
Lies den Scheitelpunkt ab. Setze dessen Koordinaten in den Funktionsterm <math>f(x)=a(x-d)^2+e</math> ein. | |||
|2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
{{Lösung versteckt|1=<math>f(x)=\frac{1}{5} \cdot x^2-3.5</math> | |||
<math>g(x)=(x+4)^2+0.5</math> | |||
<math>h(x)=-5(x-2)^2+10</math>|2=Lösung anzeigen|3=Lösung verbergen}}}} | |||
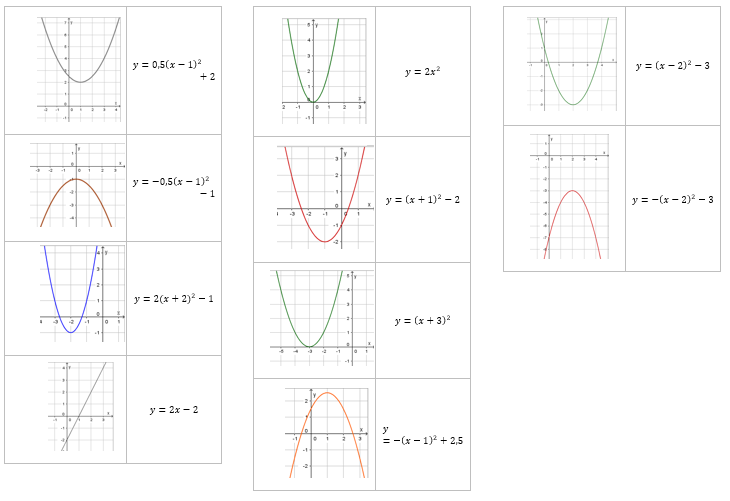
{{Übung|In diesem Applet sind verschiedene Graphen abgebildet. Ermittle die zugehörigen Funktionsterme und trage sie in die Felder unter den jeweiligen Graphen ein. | |||
<math> | '''Hinweise:''' | ||
::'''1. Beginne jeden Term mit <math>y=</math>''' | |||
::'''2. Wenn du ein "hoch 2" einfügen möchtest, schreibe ^2.''' | |||
{{LearningApp|app=p8guq0hdn17|width=100%|height=600px}} | |||
{{Lösung versteckt|[[Datei:Lösung Applet Finde den Term.PNG|rahmenlos|800px|Lösung zu Applet]]}} | |||
|3=Üben}} | |||
{{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S.19)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
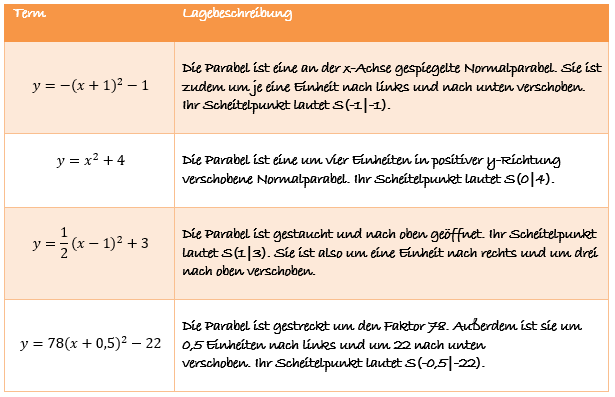
Vervollständige die Tabelle: | |||
[[Datei:Übung Lagebeschreibung.PNG|rahmenlos|750px|Übungsaufgabe]] | |||
{{Lösung versteckt|[[Datei:Übung Lagebeschreibung Lsg.PNG|rahmenlos|750px|Lösungsvorschlag]]}} | |||
}} | |||
===Die Parameter der Normalform=== | |||
{{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 19)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
Zwei Parabeln sollen den gleichen y-Achsenabschnitt c haben. Gib je zwei Funktionsterme in Normalform an. | |||
'''a)''' <math>c=1</math> '''b)''' <math>c=-2,5</math> '''c)''' <math>c=-4</math> '''d)''' <math>c=\frac{3}{5}</math> '''e)''' <math>c=0</math> | |||
{{Lösung versteckt|1=Deine Terme können ganz anders aussehen, als die Terme hier in den Lösungsvorschlägen. Wichtig ist, dass deine zwei Terme jeweils den gleichen y-Achsenabschnitt <math>c</math> wie angegeben haben. Die Parameter <math>a</math> und <math>b</math> können dann beliebig variiert werden. | |||
<math> | {{{!}} class="wikitable" | ||
{{!}}- | |||
{{!}}'''a)'''{{!}}{{!}} <math>y=x^2+2x+1</math> {{!}}{{!}} '''b)'''{{!}}{{!}} <math>y=-x^2+2x-2,5</math> {{!}}{{!}} '''c)'''{{!}}{{!}} <math>y=2x^2-2x-4</math> | |||
{{!}}- | |||
{{!}} {{!}}{{!}} <math>y=2x^2+2x+1</math> {{!}}{{!}} {{!}}{{!}} <math>y=x^2-x-2,5</math>{{!}}{{!}} {{!}}{{!}} <math>y=2x^2-3x-4</math> | |||
{{!}}} | |||
{{{!}} class="wikitable" | |||
{{!}}- | |||
{{!}}'''d)'''{{!}}{{!}} <math>y=-x^2+x+\frac{3}{5}</math> {{!}}{{!}} '''e)'''{{!}}{{!}} <math>y=-x^2+x</math> | |||
{{!}}- | |||
{{!}} {{!}}{{!}} <math>y=-x^2+5x+\frac{3}{5}</math> {{!}}{{!}} {{!}}{{!}} <math>y=x^2-x</math> | |||
{{!}}}|2=Lösung anzeigen|3=Lösung verbergen}}|Arbeitsmethode | |||
}} | |||
{{Übung| | {{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 20) und einen Partner''' [[Datei:Notepad-117597.svg|32x32px]][[Datei:Puzzle-1020221_640.jpg|rahmenlos|80x80px]]. | ||
'''a)''' Denke dir drei Funktionsterme in Normalform aus. | |||
{{Lösung versteckt|1=Terme in Normalform quadratischer Funktionen sehen allgemein so aus: <math>y=ax^2+bx+c</math>. | |||
Denke dir Werte für die Parameter <math>a, b</math> und <math>c</math> aus und setze sie ein. | |||
'''Beispiel:''' Für <math>a=1</math>, <math>b=1</math> und <math>c=-4</math> erhält man: <math>y=1\cdot x^2+1\cdot x-4</math>.|2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
'''b)''' Gib deinem Partner deine Funktionsterme und nimm dafür seine. Zeichnet die Graphen zu den Termen. | |||
{{Lösung versteckt|Zur Kontrolle kannst du das unten stehende '''GeoGebra-Applet''' benutzen. Gib die Parameter der Funktionsterme ein und vergleiche deinen Graph mit dem Ergebnis im Applet.|Lösung anzeigen|Lösung verbergen}} | |||
'''c)''' Vergleicht eure Ergebnisse und erklärt Schritt-für-Schritt wie ihr die Graphen erstellt habt. Notiert eine gemeinsame Schritt-für-Schritt-Anleitung in euren Hefter. | |||
{{Lösung versteckt | |||
|Eine Anleitung kann wie folgt aussehen. | |||
#y-Achsenabschnitt P(0;c) ablesen. | |||
#Verschiedene x-Werte in den Term einsetzen und so die zugehörigen y-Werte bestimmen (Erstellen einer Tabelle). | |||
#Koordinatensystem zeichnen und Punkte eintragen. | |||
#Punkte zu einer Parabel verbinden.|Lösung anzeigen|Lösung verbergen}}}} | |||
<ggb_applet id="GBnam42z" width="750" height="499" border="888888" /> | |||
===Allgemeine Übungen zu Parametern=== | |||
{{Übung|Teste dein Wissen und werde Punkte-Millionär. Schaffst du es ins Finale? | |||
{{LearningApp|app=phcsyj21c17|width=100%|height=500px}} | |||
}} | |||
{{Übung|'''Für diese | {{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 21) und einen Partner''' [[Datei:Notepad-117597.svg|32x32px]][[Datei:Puzzle-1020221_640.jpg|rahmenlos|80x80px]]. | ||
'''a)''' Denke dir zwei Terme quadratischer Funktionen aus und notiere eine Lagebeschreibung des Graphen. | '''a)''' Denke dir zwei Terme quadratischer Funktionen aus und notiere eine Lagebeschreibung des Graphen. | ||
< | {{Lösung versteckt|Die Parabel ist eine an der x-Achse gespiegelte Normalparabel. Sie ist um je eine Einheit nach rechts und nach oben verschoben. Ihr Scheitelpunkt lautet <math>S(1;1)</math>.|Beispiel anzeigen|Beispiel verbergen}} | ||
'''b)''' Tausche deine Beschreibungen (nicht den Term!) mit denen deines Partners aus und bestimme seine Funktionsterme. | '''b)''' Tausche deine Beschreibungen (nicht den Term!) mit denen deines Partners aus und bestimme seine Funktionsterme. | ||
{{Lösung versteckt|1=Die Lösung zu dem Beispiel in Übungsteil a) lautet: <math>y=(x-1)^2+1</math>.|2=Beispiel anzeigen|3=Beispiel verbergen}} | |||
'''c)''' Kontrolliert eure Ergebnisse gegenseitig. Habt ihr die richtigen Terme gefunden? Wenn nicht, versucht gemeinsam eure Fehler aufzudecken und zu klären. | '''c)''' Kontrolliert eure Ergebnisse gegenseitig. Habt ihr die richtigen Terme gefunden? Wenn nicht, versucht gemeinsam eure Fehler aufzudecken und zu klären. | ||
{{Lösung versteckt|Schaut euch noch einmal die Merksätze auf den Parameterseiten der [[Mathematik-digital/Quadratische Funktionen erkunden/Die Parameter der Normalform|Normalform]] und der [[Mathematik-digital/Quadratische Funktionen erkunden/Die Parameter der Scheitelpunktform|Scheitelpunktform]] an.|Hilfe anzeigen|Hilfe verbergen}}}} | |||
==Von der Scheitelpunkt- zur Normalform== | |||
{{Box|Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 22)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
Forme die folgenden Terme in Scheitelpunktform in Normalform um: | |||
<math>(1)y=(x-2)^2+3</math> <math>(4)y=(x-1,5)^2-7</math> <math>(7)y=(x+4)^2+2</math> | |||
<math>(2)y=-(x+5)^2+25</math> <math>(5)y=2(x+7)^2-35</math> <math>(8)y=-3(x-6)^2</math> | |||
<math>(3)y=4(x-1)^2+0,5</math> <math>(6)y=(x+0,5)^2+0,75</math> <math>(9)y=0,5(x-2)^2-16</math> | |||
{{Lösung versteckt|1= | |||
{{{!}} class="wikitable" | |||
{{!}}- | |||
{{!}}'''Funktionsterm (1)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' {{!}}{{!}}'''Funktionsterm (6)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' | |||
{{!}}- | |||
{{!}}<math>y=(x-2)^2+3</math>{{!}}{{!}} Klammer auflösen {{!}}{{!}}<math>y=(x+0,5)^2+0,75</math>{{!}}{{!}} Klammer auflösen | |||
{{!}}- | |||
{{!}}<math>=(x-2)(x-2)+3</math>{{!}}{{!}} Klammer ausmultiplizieren {{!}}{{!}}<math>=(x+0,5)(x+0,5)+0,75</math>{{!}}{{!}} Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=x^2-2x-2x+4+3</math>{{!}}{{!}} Zusammenfassen {{!}}{{!}}<math>=x^2+0,5x+0,5x+0,25+0,75</math>{{!}}{{!}} Zusammenfassen | |||
{{!}}- | |||
{{!}}<math>=x^2-4x+7</math>{{!}}{{!}} {{!}}{{!}}<math>=x^2+x+1</math> | |||
{{!}}} | |||
{{{!}} class="wikitable" | |||
{{!}}- | |||
{{!}}'''Funktionsterm (2)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' {{!}}{{!}}'''Funktionsterm (7)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' | |||
{{!}}- | |||
{{!}}<math>y=-(x+5)^2+25</math>{{!}}{{!}} Klammer auflösen {{!}}{{!}}<math>y=(x+4)^2+2</math>{{!}}{{!}} Klammer auflösen | |||
{{!}}- | |||
{{!}}<math>=-((x+5)(x+5))+25</math>{{!}}{{!}} innere Klammer ausmultiplizieren {{!}}{{!}}<math>=(x+4)(x+4)^2+2</math>{{!}}{{!}} Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=-(x^2+5x+5x+25)+25</math>{{!}}{{!}} Klammer ausmultiplizieren {{!}}{{!}}<math>=x^2+4x+4x+16+2</math>{{!}}{{!}} Zusammenfassen | |||
{{!}}- | |||
{{!}}<math>=-x^2-10x-25+25</math>{{!}}{{!}} Zusammenfassen {{!}}{{!}}<math>=x^2+8x+18</math>{{!}}{{!}} | |||
{{!}}- | |||
{{!}}<math>=-x^2-10x</math>{{!}}{{!}} {{!}}{{!}} | |||
{{!}}} | |||
{{{!}} class="wikitable" | |||
{{!}}- | |||
{{!}}'''Funktionsterm (3)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' {{!}}{{!}}'''Funktionsterm (8)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' | |||
{{!}}- | |||
{{!}}<math>y=4(x-1)^2+0,5</math>{{!}}{{!}} Klammer auflösen {{!}}{{!}}<math>y=-3(x-6)^2</math>{{!}}{{!}} Klammer auflösen | |||
{{!}}- | |||
{{!}}<math>=4((x-1)(x-1))+0,5</math>{{!}}{{!}} innere Klammer ausmultiplizieren {{!}}{{!}}<math>=-3((x-6)(x-6))</math>{{!}}{{!}} innere Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=4(x^2-x-x+1)+0,5</math>{{!}}{{!}} Klammer ausmultiplizieren {{!}}{{!}}<math>=-3(x^2-6x-6x+36)</math>{{!}}{{!}} Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=4x^2-4x-4x+4+0,5</math>{{!}}{{!}} Zusammenfassen {{!}}{{!}}<math>=-3x^2+18x+18x-108</math>{{!}}{{!}} Zusammenfassen | |||
{{!}}- | |||
{{!}}<math>=4x^2-8x+4,5</math>{{!}}{{!}} {{!}}{{!}}<math>=-3x^2+36x-108</math> | |||
{{!}}} | |||
{{{!}} class="wikitable" | |||
{{!}}- | |||
{{!}}'''Funktionsterm (4)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' {{!}}{{!}}'''Funktionsterm (9)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' | |||
{{!}}- | |||
{{!}}<math>y=(x-1,5)^2-7</math>{{!}}{{!}} Klammer auflösen {{!}}{{!}}<math>y=0,5(x-2)^2-16</math>{{!}}{{!}} Klammer auflösen | |||
{{!}}- | |||
{{!}}<math>=(x-1,5)(x-1,5)-7</math>{{!}}{{!}} Klammer ausmultiplizieren {{!}}{{!}}<math>0,5((x-2)(x-2))-16</math>{{!}}{{!}} innere Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=x^2-1,5x-1,5x+2,25-7</math>{{!}}{{!}} Zusammenfassen {{!}}{{!}}<math>=0,5(x^2-2x-2x+4)-16</math>{{!}}{{!}} Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=x^2-3x-4,75</math>{{!}}{{!}} {{!}}{{!}}<math>=0,5x^2-x-x+2-16</math>{{!}}{{!}} Zusammenfassen | |||
{{!}}- | |||
{{!}} {{!}}{{!}} {{!}}{{!}}<math>=0,5x^2-2x-14</math> | |||
{{!}}} | |||
{{{!}} class="wikitable" | |||
{{!}}- | |||
{{!}}'''Funktionsterm (5)'''{{!}}{{!}} '''Schritt-für-Schritt-Anleitung''' | |||
{{!}}- | |||
{{!}}<math>y=2(x+7)^2-35</math>{{!}}{{!}} Klammer auflösen | |||
{{!}}- | |||
{{!}}<math>=2((x+7)(x+7))-35</math>{{!}}{{!}} Klammer ausmultiplizieren | |||
{{!}}- | |||
{{!}}<math>=2(x^2+7x+7x+49)-35</math> | |||
{{!}}- | |||
{{!}}<math>=2x^2+14x+14x+98-35</math>{{!}}{{!}} Zusammenfassen | |||
{{!}}- | |||
{{!}}<math>=2x^2+28x+63</math> | |||
{{!}}}|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Üben}} | |||
==Quadratische Funktionen anwenden== | |||
{{Box|Übung|Diese Aufgabe befindet sich auch in den Kapiteln zur [[Mathematik-digital/Quadratische Funktionen erkunden/Die Scheitelpunktform|Scheitelpunktform]] und zur [[Mathematik-digital/Quadratische Funktionen erkunden/Die Normalform|Normalform]]. Du kannst sie hier erneut als Übung verwenden, indem du die Bilder bearbeitest, die du dort ausgelassen hast. | |||
Finde Werte für a, d und e, so dass <math>f(x)</math> die Kurve auf dem Bild möglichst gut beschreibt. | Finde Werte für a, d und e bzw. a, b und c, so dass <math>f(x)</math> bzw. <math>g(x)</math> die Kurve auf dem Bild möglichst gut beschreibt. | ||
< | <ggb_applet id="Jymnn6u8" width="895" height="610" border="888888" /> | ||
{{Lösung versteckt|1=Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben. | |||
Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben. | |||
'''Scheitelpunktform:''' | '''Scheitelpunktform:''' | ||
{ | {{{!}} class="wikitable" | ||
{{!}}- | |||
! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter d !! Parameter e | ! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter d !! Parameter e | ||
{{!}}- | |||
{{!}} Angry Birds {{!}}{{!}} <math>f(x)=-0.13(x-7)^2+4.85</math> {{!}}{{!}} -0.15 ≤ a ≤ -0.13 {{!}}{{!}} 6.80 ≤ d ≤ 7.20 {{!}}{{!}} 4.70 ≤ e ≤ 5.00 | |||
{{!}}- | |||
{{!}} Golden Gate Bridge {{!}}{{!}} <math>f(x)=0.04(x-5.7)^2+1</math> {{!}}{{!}} 0.03 ≤ a ≤ 0.05 {{!}}{{!}} 5.00 ≤ d ≤ 6.40 {{!}}{{!}} 0.80 ≤ e ≤ 1.10 | |||
{{!}}- | |||
{{!}} Springbrunnen {{!}}{{!}} <math>f(x)=-0.33(x-4,85)^2+5.3</math> {{!}}{{!}} -0.40 ≤ a ≤ -0.30 {{!}}{{!}} 4.70 ≤ d ≤ 5.00 {{!}}{{!}} 5.10 ≤ e ≤ 5.50 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen links) {{!}}{{!}} <math>f(x)=0.40(x-2,50)^2+4.35</math> {{!}}{{!}} 0.33 ≤ a ≤ 0.47 {{!}}{{!}} 2.40 ≤ d ≤ 2.60 {{!}}{{!}} 4.25 ≤ e ≤ 4.40 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen mitte) {{!}}{{!}} <math>f(x)=0.33(x-5.85)^2+3.4</math> {{!}}{{!}} 0.30 ≤ a ≤ 0.36 {{!}}{{!}} 5.70 ≤ d ≤ 6.00 {{!}}{{!}} 3.20 ≤ e ≤ 3.60 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen rechts) {{!}}{{!}} <math>f(x)=0.22(x-9,40)^2+3.60</math> {{!}}{{!}} 0.18 ≤ a ≤ 0.27 {{!}}{{!}} 9.30 ≤ d ≤ 9.50 {{!}}{{!}} 3.55 ≤ e ≤ 3.65 | |||
{{!}}- | |||
{{!}} Gebirgsformation {{!}}{{!}} <math>f(x)=-0.2(x-5.4)^2+2.3</math> {{!}}{{!}} -0.30 ≤ a ≤ -0.10 {{!}}{{!}} 5.10 ≤ d ≤ 5.70 {{!}}{{!}} 2.10 ≤ e ≤ 2.50 | |||
{{!}}- | |||
{{!}} Motorrad-Stunt {{!}}{{!}} <math>f(x)=-0.07(x-7.7)^2+5.95</math> {{!}}{{!}} -0.10 ≤ a ≤ -0.04 {{!}}{{!}} 7.30 ≤ d ≤ 8.10 {{!}}{{!}} 5.70 ≤ e ≤ 6.20 | |||
{{!}}- | |||
{{!}} Basketball {{!}}{{!}} <math>f(x)=-0.32(x-6.5)^2+6.45</math> {{!}}{{!}} -0.35 ≤ a ≤ -0.29 {{!}}{{!}} 6.20 ≤ d ≤ 6.80 {{!}}{{!}} 6.20 ≤ e ≤ 6.70 | |||
{{!}}} | |||
'''Normalform:''' | '''Normalform:''' | ||
{ | {{{!}} class="wikitable" | ||
{{!}}- | |||
! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter b !! Parameter c | ! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter b !! Parameter c | ||
{{!}}- | |||
{{!}} Angry Birds {{!}}{{!}} <math>f(x)=-0.13x^2+1.82x-1.52</math> {{!}}{{!}} -0.14 ≤ a ≤ -0.13 {{!}}{{!}} 1.82 ≤ b ≤ 1.95 {{!}}{{!}} -1.85 ≤ c ≤ -1.52 | |||
{{!}}- | |||
{{!}} Golden Gate Bridge {{!}}{{!}} <math>f(x)=0.04x^2-0.46x+2.30</math> {{!}}{{!}} 0.03 ≤ a ≤ 0.05 {{!}}{{!}} -0.40 ≤ b ≤ -0.50 {{!}}{{!}} 2.05 ≤ c ≤ 2.30 | |||
{{!}}- | |||
{{!}} Springbrunnen {{!}}{{!}} <math>f(x)=-0.33x^2+3.20x-2.46</math> {{!}}{{!}} -0.40 ≤ a ≤ -0.30 {{!}}{{!}} 3.15 ≤ b ≤ 3.35 {{!}}{{!}} -2.95 ≤ c ≤ -2.45 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen links){{!}}{{!}} <math>f(x)=0.40x^2-2.00x+6.85</math> {{!}}{{!}} 0.33 ≤ a ≤ 0.47 {{!}}{{!}} 1.80 ≤ b ≤ 2.00 {{!}}{{!}} 6.35 ≤ c ≤ 6.85 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen mitte){{!}}{{!}} <math>f(x)=0.33x^2-3.86x+14.69</math> {{!}}{{!}} 0.30 ≤ a ≤ 0.36 {{!}}{{!}} -4.10 ≤ b ≤ -3.60 {{!}}{{!}} 13.65 ≤ c ≤ 14.95 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen rechts){{!}}{{!}} <math>f(x)=0.22x^2-4.14x+23.04</math> {{!}}{{!}} 0.18 ≤ a ≤ 0.27 {{!}}{{!}} -3.40 ≤ b ≤ -5.05 {{!}}{{!}} 19.70 ≤ c ≤ 27.20 | |||
{{!}}- | |||
{{!}} Gebirgsformation {{!}}{{!}} <math>f(x)=-0.2x^2+2.16x-3.53</math> {{!}}{{!}} -0.30 ≤ a ≤ -0.15 {{!}}{{!}} 1.55 ≤ b ≤ 3.30 {{!}}{{!}} -6.35 ≤ c ≤ -1.70 | |||
{{!}}- | |||
{{!}} Motorrad-Stunt {{!}}{{!}} <math>f(x)=-0.07x^2+1.08x+1.79</math> {{!}}{{!}} -0.10 ≤ a ≤ -0.04 {{!}}{{!}} 0.85 ≤ b ≤ 1.30 {{!}}{{!}} 0.95 ≤ c ≤ 1.79 | |||
{{!}}- | |||
{{!}} Basketball {{!}}{{!}} <math>f(x)=-0.32x^2+4.16x-7.07</math> {{!}}{{!}} -0.35 ≤ a ≤ -0.29 {{!}}{{!}} 3.80 ≤ b ≤ 4.40 {{!}}{{!}} -7.40 ≤ c ≤ -6.10 | |||
|} | {{!}}}|2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} | ||
</ | |Üben}} | ||
{{Übung|'''Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 23)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
[[Datei:Aufgabe Terrasse für Kiosk.PNG|rahmenlos|700px|Übungsaufgabe]] | |||
{{Lösung versteckt|1='''a)''' <math>A(2)=2 \cdot (20-2)=2 \cdot 18=36</math>, | |||
<math>A(4)=4 \cdot (20-4)=4 \cdot 16=64</math>, | |||
<math>A(10)=10 \cdot (20-10)=10 \cdot 10=100</math> | |||
Für <math>x=2m</math> beträgt der Flächeninhalt der Terrasse <math>36m^2</math>. Ist die Seitenlänge <math>x=4m</math>, dann beträgt der Flächeninhalt der Terrasse <math>64m^2</math>. Bei einer Seitenlänge von <math>x=10m</math> beträgt der Flächeninhalt <math>100m^2</math>. | |||
Hinweis: Hier kannst du auch andere Werte x eingesetzt haben. Um eine sinnvolle Lösung zu erhalten darf x weder kleiner <math>0m</math> noch größer als <math>20m</math> sein. In den Fällen würdest du einen negativen Flächeninhalt erhalten. | |||
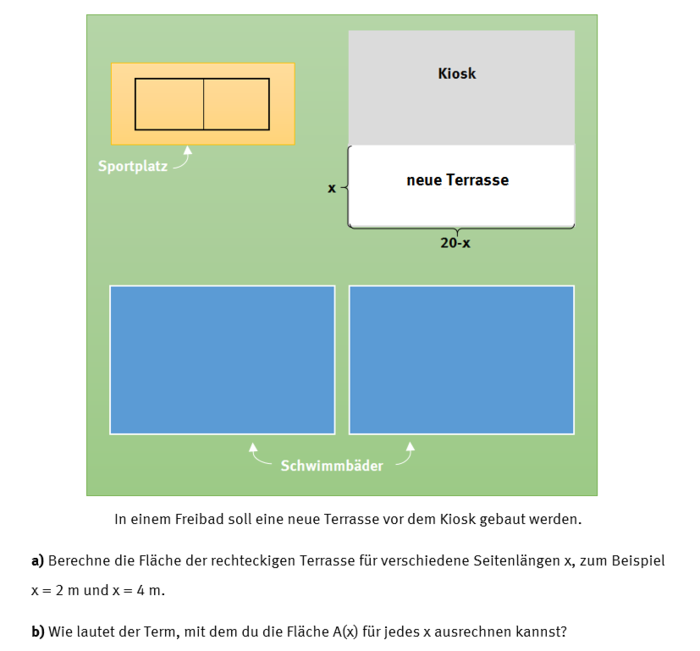
'''b)''' <math>A(x)=x \cdot (20-x)</math> | |||
Für den Flächeninhalt eines Rechtecks gilt: <math>A=a \cdot b</math>, wobei a und b die Seitenlängen des Rechtecks beschreiben. Für die Terrasse gilt: <math>a=x</math> und <math>b=20-x</math>.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
}} | |||
Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]]) | |||
[[Kategorie:Quadratische Funktion]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:LearningApps]] | |||
[[Kategorie:GeoGebra]] | |||
Aktuelle Version vom 30. März 2022, 21:39 Uhr
In diesem Kapitel des Lernpfads findest du Übungsaufgaben zu allen Inhalten, die du in den vorherigen Abschnitten kennengelernt hast. Sie sollen dir helfen, dein Wissen zu festigen. Klicke im Inhaltsverzeichnis einfach auf das Thema, zu dem du Übungsaufgaben bearbeiten möchtest.
Hinweis: Du musst nicht alle Aufgaben dieser Seite bearbeiten. Suche dir gezielt Aufgaben zum Üben heraus.
Parameter
Die Parameter der Scheitelpunktform
Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 17) ![]() .
.
Zeichne die Graphen der folgenden Funktionen:
a) b) c)
d) e) f) g)
Schaue dir die Merksätze zu den Parametern und in deinem Hefter noch einmal an. Dadurch kannst du herausfinden wie die Parabel, die du zeichnen möchtest aussehen muss.
Ermittle einzelne Punkte oder lege eine Wertetabelle an, um die Parabeln zu zeichnen.Gib für die Parameter und die Werte im Applet an, so dass g(x) einem der Funktionsterme (a)-(g) gleicht. Vergleiche zur Kontrolle die Parabel im Applet mit deiner gezeichneten Parabel.

Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 18) ![]() .
.
In dieser Aufgabe werden die Parameter kombiniert, die du in dem Kapitel Die Parameter der Scheitelpunktform kennengelernt hast. Gegeben ist die Wertetabelle:
a) Zeichne die Graphen zu den Funktionen f(x), g(x) und h(x) in das Koordinatensystem in deinem Hefter. Nicht alle y-Werte können sinnvoll in den Ausschnitt, der in dem Koordinatensystem gezeigt wird, eingetragen werden.
b) Bestimme die Funktionsterme in Scheitelpunktform.
Ist der Graph gestreckt, gestaucht und/oder gespiegelt? Durch die Beantwortung dieser Frage kannst du den Wert des Parameters eingrenzen. Anschließend findest du den genauen Wert zum Beispiel durch systematisches Probieren und Abgleichen mit den gegebenen Funktionswerten in der Tabelle.
Lies den Scheitelpunkt ab. Setze dessen Koordinaten in den Funktionsterm ein.
Die Parameter der Normalform
Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 19) ![]() .
.
Zwei Parabeln sollen den gleichen y-Achsenabschnitt c haben. Gib je zwei Funktionsterme in Normalform an.
a) b) c) d) e)
Deine Terme können ganz anders aussehen, als die Terme hier in den Lösungsvorschlägen. Wichtig ist, dass deine zwei Terme jeweils den gleichen y-Achsenabschnitt wie angegeben haben. Die Parameter und können dann beliebig variiert werden.
| a) | b) | c) | |||
| d) | e) | ||
Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 20) und einen Partner ![]()
 .
.
a) Denke dir drei Funktionsterme in Normalform aus.
Terme in Normalform quadratischer Funktionen sehen allgemein so aus: . Denke dir Werte für die Parameter und aus und setze sie ein.
Beispiel: Für , und erhält man: .b) Gib deinem Partner deine Funktionsterme und nimm dafür seine. Zeichnet die Graphen zu den Termen.
c) Vergleicht eure Ergebnisse und erklärt Schritt-für-Schritt wie ihr die Graphen erstellt habt. Notiert eine gemeinsame Schritt-für-Schritt-Anleitung in euren Hefter.
Eine Anleitung kann wie folgt aussehen.
- y-Achsenabschnitt P(0;c) ablesen.
- Verschiedene x-Werte in den Term einsetzen und so die zugehörigen y-Werte bestimmen (Erstellen einer Tabelle).
- Koordinatensystem zeichnen und Punkte eintragen.
- Punkte zu einer Parabel verbinden.

Allgemeine Übungen zu Parametern
Teste dein Wissen und werde Punkte-Millionär. Schaffst du es ins Finale?
Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 21) und einen Partner ![]()
 .
.
a) Denke dir zwei Terme quadratischer Funktionen aus und notiere eine Lagebeschreibung des Graphen.
b) Tausche deine Beschreibungen (nicht den Term!) mit denen deines Partners aus und bestimme seine Funktionsterme.
c) Kontrolliert eure Ergebnisse gegenseitig. Habt ihr die richtigen Terme gefunden? Wenn nicht, versucht gemeinsam eure Fehler aufzudecken und zu klären.
Von der Scheitelpunkt- zur Normalform
Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 22) ![]() .
.
Forme die folgenden Terme in Scheitelpunktform in Normalform um:
| Funktionsterm (1) | Schritt-für-Schritt-Anleitung | Funktionsterm (6) | Schritt-für-Schritt-Anleitung |
| Klammer auflösen | Klammer auflösen | ||
| Klammer ausmultiplizieren | Klammer ausmultiplizieren | ||
| Zusammenfassen | Zusammenfassen | ||
| Funktionsterm (2) | Schritt-für-Schritt-Anleitung | Funktionsterm (7) | Schritt-für-Schritt-Anleitung |
| Klammer auflösen | Klammer auflösen | ||
| innere Klammer ausmultiplizieren | Klammer ausmultiplizieren | ||
| Klammer ausmultiplizieren | Zusammenfassen | ||
| Zusammenfassen | |||
| Funktionsterm (3) | Schritt-für-Schritt-Anleitung | Funktionsterm (8) | Schritt-für-Schritt-Anleitung |
| Klammer auflösen | Klammer auflösen | ||
| innere Klammer ausmultiplizieren | innere Klammer ausmultiplizieren | ||
| Klammer ausmultiplizieren | Klammer ausmultiplizieren | ||
| Zusammenfassen | Zusammenfassen | ||
| Funktionsterm (4) | Schritt-für-Schritt-Anleitung | Funktionsterm (9) | Schritt-für-Schritt-Anleitung |
| Klammer auflösen | Klammer auflösen | ||
| Klammer ausmultiplizieren | innere Klammer ausmultiplizieren | ||
| Zusammenfassen | Klammer ausmultiplizieren | ||
| Zusammenfassen | |||
| Funktionsterm (5) | Schritt-für-Schritt-Anleitung |
| Klammer auflösen | |
| Klammer ausmultiplizieren | |
| Zusammenfassen | |
Quadratische Funktionen anwenden
Diese Aufgabe befindet sich auch in den Kapiteln zur Scheitelpunktform und zur Normalform. Du kannst sie hier erneut als Übung verwenden, indem du die Bilder bearbeitest, die du dort ausgelassen hast.
Finde Werte für a, d und e bzw. a, b und c, so dass bzw. die Kurve auf dem Bild möglichst gut beschreibt.

Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben.
Scheitelpunktform:
| Hintergrundbild | Lösungsvorschlag | Parameter a | Parameter d | Parameter e |
|---|---|---|---|---|
| Angry Birds | -0.15 ≤ a ≤ -0.13 | 6.80 ≤ d ≤ 7.20 | 4.70 ≤ e ≤ 5.00 | |
| Golden Gate Bridge | 0.03 ≤ a ≤ 0.05 | 5.00 ≤ d ≤ 6.40 | 0.80 ≤ e ≤ 1.10 | |
| Springbrunnen | -0.40 ≤ a ≤ -0.30 | 4.70 ≤ d ≤ 5.00 | 5.10 ≤ e ≤ 5.50 | |
| Elbphilharmonie (Bogen links) | 0.33 ≤ a ≤ 0.47 | 2.40 ≤ d ≤ 2.60 | 4.25 ≤ e ≤ 4.40 | |
| Elbphilharmonie (Bogen mitte) | 0.30 ≤ a ≤ 0.36 | 5.70 ≤ d ≤ 6.00 | 3.20 ≤ e ≤ 3.60 | |
| Elbphilharmonie (Bogen rechts) | 0.18 ≤ a ≤ 0.27 | 9.30 ≤ d ≤ 9.50 | 3.55 ≤ e ≤ 3.65 | |
| Gebirgsformation | -0.30 ≤ a ≤ -0.10 | 5.10 ≤ d ≤ 5.70 | 2.10 ≤ e ≤ 2.50 | |
| Motorrad-Stunt | -0.10 ≤ a ≤ -0.04 | 7.30 ≤ d ≤ 8.10 | 5.70 ≤ e ≤ 6.20 | |
| Basketball | -0.35 ≤ a ≤ -0.29 | 6.20 ≤ d ≤ 6.80 | 6.20 ≤ e ≤ 6.70 |
Normalform:
| Hintergrundbild | Lösungsvorschlag | Parameter a | Parameter b | Parameter c |
|---|---|---|---|---|
| Angry Birds | -0.14 ≤ a ≤ -0.13 | 1.82 ≤ b ≤ 1.95 | -1.85 ≤ c ≤ -1.52 | |
| Golden Gate Bridge | 0.03 ≤ a ≤ 0.05 | -0.40 ≤ b ≤ -0.50 | 2.05 ≤ c ≤ 2.30 | |
| Springbrunnen | -0.40 ≤ a ≤ -0.30 | 3.15 ≤ b ≤ 3.35 | -2.95 ≤ c ≤ -2.45 | |
| Elbphilharmonie (Bogen links) | 0.33 ≤ a ≤ 0.47 | 1.80 ≤ b ≤ 2.00 | 6.35 ≤ c ≤ 6.85 | |
| Elbphilharmonie (Bogen mitte) | 0.30 ≤ a ≤ 0.36 | -4.10 ≤ b ≤ -3.60 | 13.65 ≤ c ≤ 14.95 | |
| Elbphilharmonie (Bogen rechts) | 0.18 ≤ a ≤ 0.27 | -3.40 ≤ b ≤ -5.05 | 19.70 ≤ c ≤ 27.20 | |
| Gebirgsformation | -0.30 ≤ a ≤ -0.15 | 1.55 ≤ b ≤ 3.30 | -6.35 ≤ c ≤ -1.70 | |
| Motorrad-Stunt | -0.10 ≤ a ≤ -0.04 | 0.85 ≤ b ≤ 1.30 | 0.95 ≤ c ≤ 1.79 | |
| Basketball | -0.35 ≤ a ≤ -0.29 | 3.80 ≤ b ≤ 4.40 | -7.40 ≤ c ≤ -6.10 |
Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 23) ![]() .
.
a) ,
,
Für beträgt der Flächeninhalt der Terrasse . Ist die Seitenlänge , dann beträgt der Flächeninhalt der Terrasse . Bei einer Seitenlänge von beträgt der Flächeninhalt .
Hinweis: Hier kannst du auch andere Werte x eingesetzt haben. Um eine sinnvolle Lösung zu erhalten darf x weder kleiner noch größer als sein. In den Fällen würdest du einen negativen Flächeninhalt erhalten.
b)
Erstellt von: Elena Jedtke (Diskussion)