Quadratische Funktionen erkunden/Quadratische Funktionen kennenlernen: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Einführung in die | {{Navigation verstecken|{{Einführung in die quadratischen}}}} | ||
__NOTOC__ | __NOTOC__ | ||
Dazu zeichnen wir ein Quadrat mit der Seitenlänge 1 cm und berechnen dessen [http://www.mathematik-wissen.de/flaecheninhalt_quadrat.htm Flächeninhalt]: | |||
:::[[Datei:Quadrat mit 1.jpg|rahmenlos|80px|Fläche 1]] | |||
:::A = 1 cm ⋅ 1 cm = 1<sup>2</sup> cm<sup>2</sup>= 1 cm<sup>2</sup> | |||
Dasselbe können wir nun mit Quadraten der Seitenlängen 2 cm, 3 cm und 4 cm machen und die Werte in einer Tabelle zusammenfassen: | |||
:::{| class="wikitable float left" | :::{| class="wikitable float left" | ||
|- style="background-color:#FFFFFF" | |- style="background-color:#FFFFFF" | ||
! style="width:7em" | | ! style="width:7em" |Seitenlänge!! style="width:7em" |Fläche | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |1 cm|| style="text-align:center" |1 cm<sup>2</sup> | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |2 cm|| style="text-align:center" |4 cm<sup>2</sup> | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |3 cm|| style="text-align:center" |9 cm<sup>2</sup> | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |4 cm|| style="text-align:center" |16 cm<sup>2</sup> | ||
|} | |||
Für ein beliebiges Quadrat kann man die Seitenlänge mit x bezeichnen. Mit der Formel für den Flächeninhalt des Quadrates ergibt sich dann A = x<sup>2</sup>. Den Flächeninhalt kannst du als '''Funktion von x''' ansehen und '''f(x) = x<sup>2</sup>''' oder '''y = x<sup>2</sup>''' schreiben. [[Datei:Quadrat mit x.jpg|rahmenlos|80px|Fläche x^2]] | |||
:::{| class="wikitable" | |||
|- style="background-color:#FFFFFF" | |||
! style="width:7em" |x!! style="width:7em" |y = x<sup>2</sup> | |||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |1|| style="text-align:center" |1 | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |2|| style="text-align:center" |4 | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |3|| style="text-align:center" |9 | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |4|| style="text-align:center" |16 | ||
|} | |} | ||
===Wie sieht der Graph über den Flächeninhalt eines Quadrates mit der Seitenlänge x aus?=== | |||
=== | |||
<div class="box arbeitsmethode"> | <div class="box arbeitsmethode"> | ||
==Aufgabe 1== | ==Aufgabe 1== | ||
'''Für diese Aufgabe benötigst du | '''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 3)''' [[Datei:Notepad-117597.svg|32x32px]]. | ||
'''a)''' Übernimm die Werte aus der Tabelle in deinen Hefter und ergänze sie um weitere Werte, die dir helfen den passenden Graphen in ein Koordinatensystem einzuzeichnen. | |||
'''a)''' Übernimm die Werte aus der Tabelle in | '''b)''' Zeichne den zugehörigen Graphen in ein Koordinatensystem. | ||
'''b)''' Zeichne den zugehörigen Graphen in ein Koordinatensystem | |||
{| class="wikitable" | {| class="wikitable" | ||
|- style="background-color:#FFFFFF" | |- style="background-color:#FFFFFF" | ||
! style="width:7em" | | ! style="width:7em" |x!! style="width:7em" |y = x<sup>2</sup> | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |1|| style="text-align:center" |1 | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |2|| style="text-align:center" |4 | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |3|| style="text-align:center" |9 | ||
|- | |- | ||
| style="text-align:center" | | | style="text-align:center" |4|| style="text-align:center" |16 | ||
|} | |} | ||
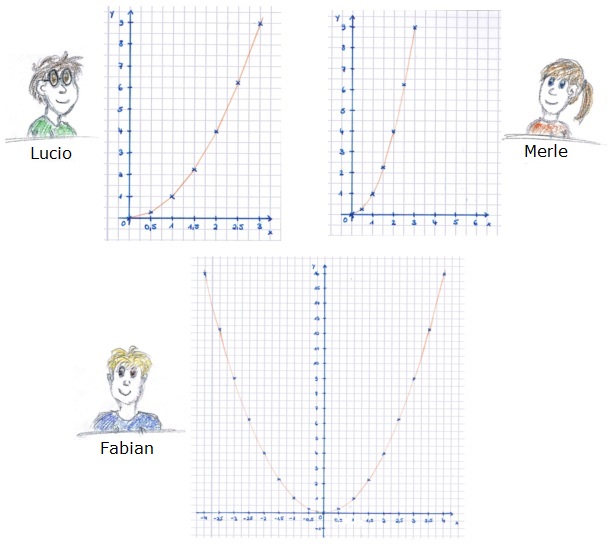
Lucio, Merle und Fabian haben unterschiedliche Lösungen zu Aufgabe 1. Schaue dir ihre Lösungen an und vergleiche, ob eine davon deiner eigenen Lösung ähnelt. | |||
{{Lösung versteckt| | |||
[[Datei:Lucio, Merle und Fabian mit ihren Lsg.jpg|rahmenlos|1500px|Lösungen]]|Lösungen von Lucio, Merle und Fabian anzeigen|Lösungen verbergen}} | |||
</div> | |||
{{Box| |Die drei diskutieren über ihre Lösungen und versuchen herauszufinden, wer von ihnen die richtige Lösung gefunden hat. Vielleicht haben ja auch mehrere recht?|Hervorhebung1}} | |||
{{Box|Aufgabe 2|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 3) und einen Partner''' [[Datei:Notepad-117597.svg|32x32px]][[Datei:Puzzle-1020221 640.jpg|80px]]. | |||
Lies dir die Argumente von Lucio, Merle und Fabian durch und führe die Unterhaltung mit deinem Partner weiter. Beachtet dabei auch eure eigenen Lösungen von Aufgabe 1 und lasst sie in eure Diskussion mit einfließen. Wer hat die richtige Lösung gefunden? | |||
Notiert eure Schlussfolgerungen in euren Heftern. Dabei solltet ihr nicht nur die Lösung aufschreiben, sondern auch die Argumente, die euch dazu geführt haben. | |||
[[Datei:Lucio, Merle und Fabian Diskussion.jpg|rahmenlos|750px|Diskussion]] | |||
{{Lösung versteckt|Bei Lucios Aussage könnte es helfen einen kleinen Ausschnitt des Graphen zu betrachten und dort noch mehr Zwischenwerte auszurechnen und einzuzeichnen. | |||
Fabians ergänzte Werte könnt ihr zum Beispiel auf mathematische Richtigkeit überprüfen und darauf, wie sie zu dem Sachzusammenhang „Quadrat“ passen.|Hilfe anzeigen|Hilfe verbergen}} | |||
{{Lösung versteckt|Bei einem Funktionsgraphen werden die einzelnen Punkte immer mit einer durchgängigen Linie verbunden. Lucios Graph sieht den anderen zwar sehr ähnlich, passt jedoch nicht ganz genau, wenn man sich noch weitere Zwischenwerte anschaut. | |||
Merles Lösung ist richtig. Es ist allerdings nicht zwingend notwendig, dass die Abstände auf den Achsen genau 1 betragen. Wichtig ist, dass die Abstände auf einer Achse alle gleich groß sind. | |||
Fabians Graph ist auch korrekt gezeichnet. Bei quadratischen Funktionen können sowohl negative als auch positive Werte für x eingesetzt werden. Fabian hat aber nicht bedacht, dass x in unserem Beispiel für die Seitenlänge eines Quadrates steht und diese nicht negativ sein kann.|Lösung anzeigen|Lösung verbergen}}|Arbeitsmethode}} | |||
===Ein paar wichtige Begriffe, die dir auf den folgenden Seiten immer wieder begegnen werden:=== | |||
</ | |||
Wir verabschieden uns nun vorerst von unserem Beispiel mit dem Flächeninhalt eines Quadrates und betrachten die allgemeine quadratische Funktion y = x<sup>2</sup>. Das heißt, du kannst jetzt auch negative Werte für die Variable x einsetzen und der Graph der quadratischen Funktion sieht aus wie in der Lösung von Fabian. | |||
{{Box|Aufgabe 3| | |||
'''Für diese Aufgabe benötigst du deinen Hefter (Merkliste, S. 1) [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
( | |||
Zeichne die Normalparabel unter den folgenden Merksatz in deinem Hefter.|Arbeitsmethode}} | |||
{{Box|Merke| | |||
* Der Term | |||
::<math>y = x^2</math> bzw. <math>f(x)=x^2</math> | |||
:beschreibt die einfachste quadratische Funktion. | |||
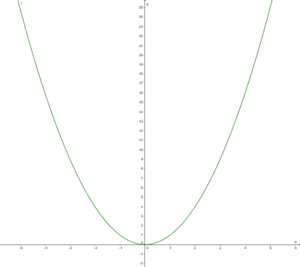
* Den Graphen dieser quadratischen Funktion nennt man '''Normalparabel'''. | |||
::[[Datei:Normalparabel grün.png|rahmenlos|mittig|300px|Normalparabel]] | |||
* Die Normalparabel hat ihren tiefsten Punkt an der Stelle <math>S(0|0)</math>. Dieser Punkt wird '''Scheitelpunkt''' genannt.|3=Merksatz}} | |||
{{Fortsetzung|weiter=Die Parameter der Scheitelpunktform|weiterlink=Quadratische Funktionen erkunden/Die Parameter der Scheitelpunktform}} | {{Fortsetzung|weiter=Die Parameter der Scheitelpunktform|weiterlink=Quadratische Funktionen erkunden/Die Parameter der Scheitelpunktform}} | ||
Version vom 25. März 2020, 11:16 Uhr
Dazu zeichnen wir ein Quadrat mit der Seitenlänge 1 cm und berechnen dessen Flächeninhalt:
Dasselbe können wir nun mit Quadraten der Seitenlängen 2 cm, 3 cm und 4 cm machen und die Werte in einer Tabelle zusammenfassen:
Seitenlänge Fläche 1 cm 1 cm2 2 cm 4 cm2 3 cm 9 cm2 4 cm 16 cm2
Für ein beliebiges Quadrat kann man die Seitenlänge mit x bezeichnen. Mit der Formel für den Flächeninhalt des Quadrates ergibt sich dann A = x2. Den Flächeninhalt kannst du als Funktion von x ansehen und f(x) = x2 oder y = x2 schreiben. 
x y = x2 1 1 2 4 3 9 4 16
Wie sieht der Graph über den Flächeninhalt eines Quadrates mit der Seitenlänge x aus?
Aufgabe 1
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 3) ![]() .
.
a) Übernimm die Werte aus der Tabelle in deinen Hefter und ergänze sie um weitere Werte, die dir helfen den passenden Graphen in ein Koordinatensystem einzuzeichnen. b) Zeichne den zugehörigen Graphen in ein Koordinatensystem.
| x | y = x2 |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Lucio, Merle und Fabian haben unterschiedliche Lösungen zu Aufgabe 1. Schaue dir ihre Lösungen an und vergleiche, ob eine davon deiner eigenen Lösung ähnelt.
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 3) und einen Partner ![]()
 .
.
Lies dir die Argumente von Lucio, Merle und Fabian durch und führe die Unterhaltung mit deinem Partner weiter. Beachtet dabei auch eure eigenen Lösungen von Aufgabe 1 und lasst sie in eure Diskussion mit einfließen. Wer hat die richtige Lösung gefunden?
Notiert eure Schlussfolgerungen in euren Heftern. Dabei solltet ihr nicht nur die Lösung aufschreiben, sondern auch die Argumente, die euch dazu geführt haben.
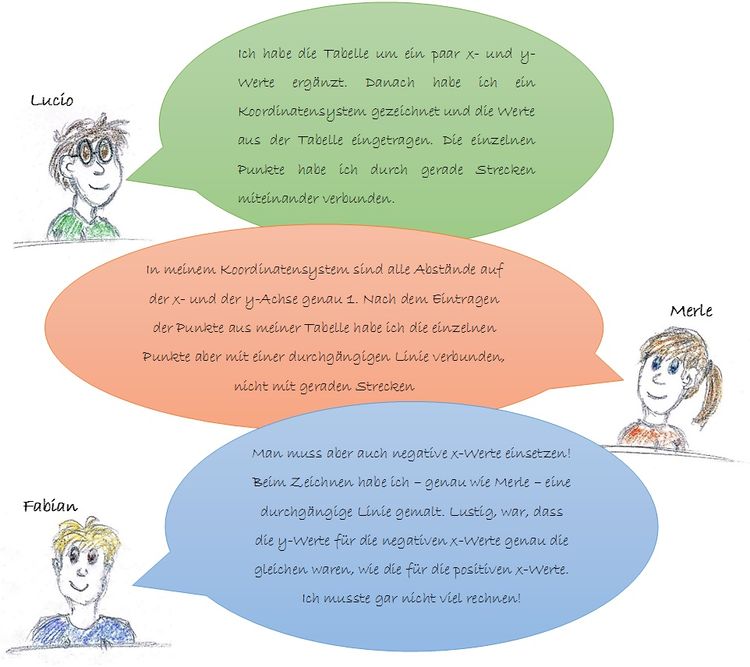
Bei Lucios Aussage könnte es helfen einen kleinen Ausschnitt des Graphen zu betrachten und dort noch mehr Zwischenwerte auszurechnen und einzuzeichnen.
Fabians ergänzte Werte könnt ihr zum Beispiel auf mathematische Richtigkeit überprüfen und darauf, wie sie zu dem Sachzusammenhang „Quadrat“ passen.Bei einem Funktionsgraphen werden die einzelnen Punkte immer mit einer durchgängigen Linie verbunden. Lucios Graph sieht den anderen zwar sehr ähnlich, passt jedoch nicht ganz genau, wenn man sich noch weitere Zwischenwerte anschaut.
Merles Lösung ist richtig. Es ist allerdings nicht zwingend notwendig, dass die Abstände auf den Achsen genau 1 betragen. Wichtig ist, dass die Abstände auf einer Achse alle gleich groß sind.
Fabians Graph ist auch korrekt gezeichnet. Bei quadratischen Funktionen können sowohl negative als auch positive Werte für x eingesetzt werden. Fabian hat aber nicht bedacht, dass x in unserem Beispiel für die Seitenlänge eines Quadrates steht und diese nicht negativ sein kann.
Ein paar wichtige Begriffe, die dir auf den folgenden Seiten immer wieder begegnen werden:
Wir verabschieden uns nun vorerst von unserem Beispiel mit dem Flächeninhalt eines Quadrates und betrachten die allgemeine quadratische Funktion y = x2. Das heißt, du kannst jetzt auch negative Werte für die Variable x einsetzen und der Graph der quadratischen Funktion sieht aus wie in der Lösung von Fabian.
Erstellt von: Elena Jedtke (Diskussion)