Signifikanztest für binomialverteilte Zufallsgrößen/Grundidee vom Signifikanztest: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
(Übung 2 hinzugefügt - noch nicht fertig)
Markierung: 2017-Quelltext-Bearbeitung
(Video 2 neu gedreht .)
Markierung: 2017-Quelltext-Bearbeitung
 
(43 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
Video 2 ! <br>
Schau dir das Video an! Es erläutert die Grundidee des Signifikanztests.
{{Box|1=Übung 1: Grundverständnis vom Testen|2=
{{#ev:youtube|KmWh7f6i0Og|800|center}}
Prüfe dein Verständnis zum Signifikanztest<br>
 
In Übung 1 kannst du überprüfen, ob du den Grundgedanken des Signifikanztests verstanden hast.<br><br>
{{Box|1=Übung 1: Grundverständnis vom Signifikanztest|2=
Kreuze jeweils die richtige Antwort an!
Kreuze jeweils die richtige Antwort an!
<div class="multiplechoice-quiz">
<div class="multiplechoice-quiz">
1. Beim Signifikanztest kann man, für den bisher angenommenen Wert, die Binomialverteilung aufschreiben. Für den Fall, dass diese Verteilung gilt, treten die Werte an den Rändern der Binomialverteilung...  
1. Beim Signifikanztest betrachtet man die Binomailverteilung für ...
(sehr unwahrscheinlich ein) (!sehr wahrscheinlich ein) (!nie ein) (!immer ein)
(die bisher angenommene bzw. geltende Wahrscheinlichkeit) (!die neu vermutete Wahrscheinlichkeit)  


2. Tritt ein Werte im Rand der Binomialverteilung ein, so wird vermutet,...
2. Für den Fall, dass die betrachtete Verteilung gilt, treten die Werte in der Mitte der Binomialverteilung...  
(!dass der bisherige angenommene Wert noch gilt) (dass der bisherige angenommene Wert sich verändert hat)  
(!sehr unwahrscheinlich ein) (sehr wahrscheinlich ein) (!nie ein) (!immer ein)


3. Liegt das Stichprobenergebnis im linken Rand der Binomialverteilung, so wird vermutet, dass 
3. Für den Fall, dass die betrachtete Verteilung gilt, treten die Werte an den Rändern der Binomialverteilung...
(der wahre Wert kleiner ist, als der bisher angenommene Wert) (!der wahre Wert größer ist, als der bisher angenommene Wert)  
(sehr unwahrscheinlich ein) (!sehr wahrscheinlich ein) (!nie ein) (!immer ein)


4. Das Ziel eines Signifikanztests ist es,  
4. Tritt ein Wert im Rand der Binomialverteilung ein, so wird vermutet,...
(der bisher angenommene Wert zu verwerfen und zu zeigen, dass sich der Wert verändert hat) (!den bisher angenommene Wert anzunehmen und zu zeigen, dass er immer noch gilt)
(!dass die bisherige geltende Wahrscheinlichkeit noch stimmt) (dass die bisherige geltende Wahrscheinlichkeit sich verändert hat)  


5. Der Verwerfungsbereich ist der Bereich, ....
5. Liegt das Ergebnis im rechten Rand der Binomialverteilung, so ..  
(indem der bisher angenommne Wert mit einer festgelegten Irrtumswahrscheinlichkeit verworfen wird) (! über den nichts ausgesagt werden darf)
(kann man mit einer großen statistischen Sicherheit sagen, dass die Wahrscheinlichkeit gestiegen ist) (!so kann man mit Sicherheit sagen, dass die Wahrscheinlichkeit gestiegen ist)  


6. Das Signifikanzniveau ist die maximale tolerierte Irrtumswahrscheinlichkeit dafür ...  
6. Liegt das Ergebnis in der Mitte der Binomialverteilung, so ....
(eine Hypothese fälschlicherweise zu verwerfen) (! eine Hypothese fälschlicherweise anzunehmen)
(! ist gezeigt, dass die bisher geltende Wahrscheinlichkeit noch stimmt) (ist keine Aussage möglich)


7. Das Signifikanzniveau ist die kumulierte Wahrscheinlichkeit des ...
7. Das Ziel eines Signifikanztests ist es,
(Verwerfungsbereichs) (! Annahmebereichs)
(zu zeigen, dass die bisher geltende Wahrscheinlichkeit sich verändert hat) (!die bisher geltende Wahrscheinlichkeit zu bestätigen)
 
      
8. Der Annahmebereich ist der Bereich, ....
(über den keine Aussage getroffen werden kann) (! indem der bisherige vermutete Wert angenommen wird)      
</div>
</div>


|3=Arbeitsmethode}}
|3=Arbeitsmethode}}


<br><br> Hast du weniger als 75% richtig, schaue dir das Video am besten nochmal an und versuche, den Test nochmal zu lösen.<br>
<br><br> Hast du weniger als 75% richtig, schaue dir das Video am besten nochmal an und versuche den Test nochmal zu lösen.<br>
Hast du 75% oder mehr richtig, kannst du weitermachen mit der nächsten Aufgabe!<br>
Hast du 75% oder mehr richtig, kannst du weitermachen mit der nächsten Aufgabe!<br>
'''Viel Spaß!'''  
'''Viel Spaß!''' <br><br>
 


{{Box|1=Übung 2: Vorbereitung für einen Signifikanztest |2=
{{Box|1=Übung 2: Grundidee eines Signifikanztests|2=
Eine Patrei sieht den Klimawandel nicht als Bedrohung an. Sie wollen daher am liebsten kein Klimaschutzprogramm in ihr Wahlprogramm aufnehmen. Aber auch sie haben die Information, dass Anfang des Jahres 2019, 71% der Menschen in Deutschland sich durch den Klimawandel bedroht gefühlt haben. Da dies kein geringer Anteil ist, beschließen sie einen Signifikanztest durchzuführen. Falls durch den Signifikanztest sich zeigen lässt, dass der Anteil im Vergleich zu Anfang des Jahres 2019 gesunken ist, wollen sie kein Klimaschutz in ihr Wahlprogramm aufnehmen.<br>
Eine Partei sieht den Klimawandel nicht als Bedrohung an. Diese Partei hat ihre Argumente gegen die Bedrohung des Klimawandels im Jahr 2019 in vielen Debatten ausführlich erläutert. Die Partei interessiert sich, ob der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019 (2019 lag der Wert bei 71%) gesunken ist. <br><br>
Hilf der Partei den Signifianztest vorzubereiten!
a) Skizziere die Binomialverteilung, die die Partei für den Signifikanztest benötigt.  
<br><br>
{{Lösung versteckt|1=Schau dir nochmal die Frage 1 in Übung 1 an.  
a) Skizziere die Binomialverteilung für den Fall, dass sich bei der Befragung immer noch 71% der Menschen in Deutschland durch den Klimawandel bedroht fühlen. Markiere zusätzlich den Bereich, indem die Partei vermutet, dass der Anteil geringer im Vergleich zu 2019 ist.  
{{Lösung versteckt|1=
[[Datei:Lösung .png|300px]]
}}
Bereche die Wahrscheinlichkeit dafür,...<br><br>
b) dass in der Stichprobe '''genau''' 710 Menschen den Klimawandel als Bedrohung ansehen.
{{Lösung versteckt|1=Nutze die Formel von Bernoulli!<br> Zur Berechnung nutze deinen Taschenrechner!
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}}
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}}
{{Lösung versteckt|1=
{{Lösung versteckt|1=
<math>P(X=710)=\tbinom{1000}{710}\cdot 0,71^{710}\cdot0,29^{290}</math><math>=0,0278</math>.<br>
[[Datei:Neueins.png|600px]]<br> Auch hier wird, wie bei der Umweltgruppe auch, die Verteilung mit der Wahrscheinlichkeit von 2019 betrachtet.  
Die Wahrscheinlichkeit, dass in der Stichprobe genau 710 Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,78 %.
}}
}}


c) Das '''höchstens''' 680 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen.
b) Markiere in der Skizze grob den Bereich rot, bei dem die Partei mit einer großen statistischen Sicherheit zeigen kann, dass der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen, gesunken ist.  
{{Lösung versteckt|1= Höchtes heißt, es können 1,2,3, ...680 der Befragten den Klimawandel als Bedrohung ansehen.<br>
Nutze zur Berechnung die Formel für die kumulierten Wahrscheinlichkeit (siehe Übung 1).<br> Nutze zur Berechnung deinen Taschenrechner!
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}}
{{Lösung versteckt|1=
{{Lösung versteckt|1=
<math>P(X\leq680)=\sum_{i=0}^{680} B_{1000,0,71} (i) = 0,0206</math><br>
[[Datei:NeuDrei.png|600px]]<br> Fühlen sich ca. höchstens 680 Menschen in der Umfrage durch den Klimawandel bedroht, so kann mit einer großen statistischen Sicherheit gesagt werden, dass der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen, im Vergleich zu 2019 gesunken ist. Hinweis! Die rote Fläche am linken Rand darf nicht zu groß sein.
Die Wahrscheinlichkeit, dass in der Stichprobe höchstens 680 der Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,06. %
}}
}}


d) Das '''mindestens''' 740 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen.
c) Liegt das Umfrageergebnis im nicht rot markierten Bereich, was kann die Partei dann für eine Aussagte treffen?
{{Lösung versteckt|1= Mindestwahrscheinlichkeiten werden über die Gegenwahrscheinlichkeit berechnet:<br> '''P(mindestens k)= 1 - P(höchstens k - 1)'''<br> Die Wahrscheinlichkeit für höchstens kannst du wieder mit dem Taschenrechner berechnen.
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}}
{{Lösung versteckt|1=
{{Lösung versteckt|1=
<math>P(X\geq740)=1-P(X\leq739)=0,0191</math><br>
In diesem Bereich kann die Partei keine Aussage treffen, da auch andere Verteilungen mit anderen Wahrscheinlichkeiten zu Grunde liegen könnten.  
Die Wahrscheinlichkeit, dass in der Stichprobe mindestens 740 Menschen den Klimawandel als Bedrohung ansehen, beträgt 1,91 %.
}}
}}


|3=Arbeitsmethode}}
|3=Arbeitsmethode}}


{{Fortsetzung|weiter=Aufbau eines Signifikanztests|weiterlink=Aufbau_eines_Signifikanztests}}
 
{{Fortsetzung|weiter=Aufbau und Durchführung eines Signifikanztests|weiterlink=Signifikanztest für binomialverteilte Zufallsgrößen/Aufbau und Durchführung eines Signifikanztests}}

Aktuelle Version vom 9. März 2020, 23:28 Uhr

Schau dir das Video an! Es erläutert die Grundidee des Signifikanztests.

Video laden
YouTube

In Übung 1 kannst du überprüfen, ob du den Grundgedanken des Signifikanztests verstanden hast.

Übung 1: Grundverständnis vom Signifikanztest

Kreuze jeweils die richtige Antwort an!

1. Beim Signifikanztest betrachtet man die Binomailverteilung für ... (die bisher angenommene bzw. geltende Wahrscheinlichkeit) (!die neu vermutete Wahrscheinlichkeit)

2. Für den Fall, dass die betrachtete Verteilung gilt, treten die Werte in der Mitte der Binomialverteilung... (!sehr unwahrscheinlich ein) (sehr wahrscheinlich ein) (!nie ein) (!immer ein)

3. Für den Fall, dass die betrachtete Verteilung gilt, treten die Werte an den Rändern der Binomialverteilung... (sehr unwahrscheinlich ein) (!sehr wahrscheinlich ein) (!nie ein) (!immer ein)

4. Tritt ein Wert im Rand der Binomialverteilung ein, so wird vermutet,... (!dass die bisherige geltende Wahrscheinlichkeit noch stimmt) (dass die bisherige geltende Wahrscheinlichkeit sich verändert hat)

5. Liegt das Ergebnis im rechten Rand der Binomialverteilung, so .. (kann man mit einer großen statistischen Sicherheit sagen, dass die Wahrscheinlichkeit gestiegen ist) (!so kann man mit Sicherheit sagen, dass die Wahrscheinlichkeit gestiegen ist)

6. Liegt das Ergebnis in der Mitte der Binomialverteilung, so .... (! ist gezeigt, dass die bisher geltende Wahrscheinlichkeit noch stimmt) (ist keine Aussage möglich)

7. Das Ziel eines Signifikanztests ist es, (zu zeigen, dass die bisher geltende Wahrscheinlichkeit sich verändert hat) (!die bisher geltende Wahrscheinlichkeit zu bestätigen)



Hast du weniger als 75% richtig, schaue dir das Video am besten nochmal an und versuche den Test nochmal zu lösen.
Hast du 75% oder mehr richtig, kannst du weitermachen mit der nächsten Aufgabe!
Viel Spaß!


Übung 2: Grundidee eines Signifikanztests

Eine Partei sieht den Klimawandel nicht als Bedrohung an. Diese Partei hat ihre Argumente gegen die Bedrohung des Klimawandels im Jahr 2019 in vielen Debatten ausführlich erläutert. Die Partei interessiert sich, ob der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019 (2019 lag der Wert bei 71%) gesunken ist.

a) Skizziere die Binomialverteilung, die die Partei für den Signifikanztest benötigt.

Schau dir nochmal die Frage 1 in Übung 1 an.
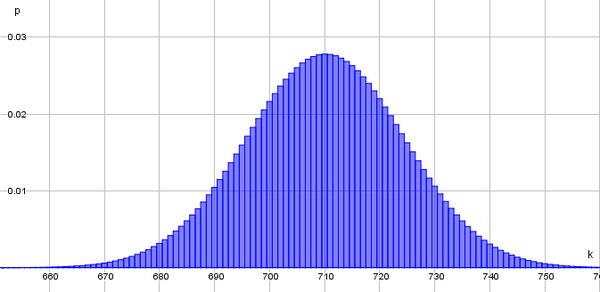
Neueins.png
Auch hier wird, wie bei der Umweltgruppe auch, die Verteilung mit der Wahrscheinlichkeit von 2019 betrachtet.

b) Markiere in der Skizze grob den Bereich rot, bei dem die Partei mit einer großen statistischen Sicherheit zeigen kann, dass der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen, gesunken ist.

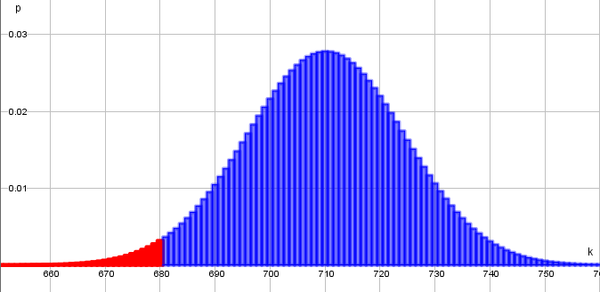
NeuDrei.png
Fühlen sich ca. höchstens 680 Menschen in der Umfrage durch den Klimawandel bedroht, so kann mit einer großen statistischen Sicherheit gesagt werden, dass der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen, im Vergleich zu 2019 gesunken ist. Hinweis! Die rote Fläche am linken Rand darf nicht zu groß sein.

c) Liegt das Umfrageergebnis im nicht rot markierten Bereich, was kann die Partei dann für eine Aussagte treffen?

In diesem Bereich kann die Partei keine Aussage treffen, da auch andere Verteilungen mit anderen Wahrscheinlichkeiten zu Grunde liegen könnten.


Aufbau und Durchführung eines Signifikanztests
Abgerufen von „https://unterrichten.zum.de/index.php?title=Signifikanztest_für_binomialverteilte_Zufallsgrößen/Grundidee_vom_Signifikanztest&oldid=111742“