Signifikanztest für binomialverteilte Zufallsgrößen/Grundidee vom Signifikanztest

Video 2 !

In Übung 1 kannst du überprüfen, ob du den Grundgedanken des Testens verstanden hast.

Übung 1: Grundverständnis vom Testen

Kreuze jeweils die richtige Antwort an!

1. Beim Signifikanztest betrachtet man die Binomailverteilung für ... (bisher angenommenen bzw. geltenden Wert) (!den neu vermuteten Wert)

2. Für den Fall, dass diese Verteilung noch gilt, treten die Werte in der Mitte der Binomialverteilung... (!sehr unwahrscheinlich ein) (sehr wahrscheinlich ein) (!nie ein) (!immer ein)

3. Für den Fall, dass diese Verteilung noch gilt, treten die Werte an den Rändern der Binomialverteilung... (sehr unwahrscheinlich ein) (!sehr wahrscheinlich ein) (!nie ein) (!immer ein)

4. Tritt ein Werte im Rand der Binomialverteilung ein, so wird vermutet,... (!dass der bisherige geltendende Wert noch stimmt) (dass der bisherige geltende Wert sich verändert hat)

5. Liegt das Stichprobenergebnis im rechten Rand der Binomialverteilung, so wird vermutet, dass (!der tatsächliche Wert kleiner ist, als der bisher geltende Wert) (der tatsächliche Wert größer ist, als der bisher geltende Wert)

6. Liegt das Ergenis im rechten Rand der Binomialverteilung, so .. (kann mit einer großen statitsichen Sicherheit sagen, dass der Wert gestiegen ist) (!so kann man mit Sicherheit sagen, dass der Wert gestiegen ist)

7.Liegt das Ergenis in der Mitte der Binomialverteilung, so .... (! ist geziegt, dass der bisher geltende Wert noch stimmt) (ist keine Aussage möglich)

8. Das Ziel eines Signifikanztests ist es, (zu zeigen, dass der bisher geltenden Wert sich verändert hat) (!den bisher geltenden Wert zu bestätigen)

Hast du weniger als 75% richtig, schaue dir das Video am besten nochmal an und versuche, den Test nochmal zu lösen.
Hast du 75% oder mehr richtig, kannst du weitermachen mit der nächsten Aufgabe!
Viel Spaß!

Übung 2: Vorüberlegungen vor der Durchführung eines Signifikanztests

Eine Patrei sieht den Klimawandel nicht als Bedrohung an. Ihre Argumente dafür, hat sie im laufe des Jahres 2019, stark öffentlich erläutert. Sie will daher am liebsten kein Klimaschutzprogramm in ihr Wahlprogramm aufnehmen. Aber auch die Patrei hat die Information, dass 2019, 71% der Deutschen sich durch den Klimawandel bedroht gefühlt haben. Da dies kein geringer Anteil ist, beschließen sie einen Signifikanztest durchzuführen. Falls durch den Signifikanztest sich zeigen lässt, dass der Anteil im Vergleich zu 2019 gesunken ist, wollen sie kein Klimaschutz in ihr Wahlprogramm aufnehmen. Sie beschließen 1000 Menschen zu befragen und legen das Signifikanzniveau auf 5% fest.

Hilf der Patrei den Signifikanztest vorzubereiten.

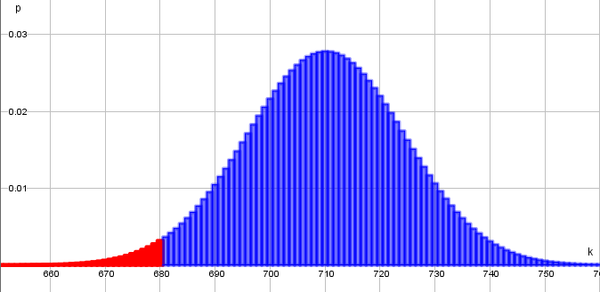
a) Übertrage in dein Heft die Skizze der Binomialverteilung für den Fall, dass sich bei der Befragung immer noch 71% der Menschen in Deutschland durch den Klimawandel bedroht fühlen. Markiere für die Partei in der Skizze grob den Verwerfungsbereich und den Annahmebereich.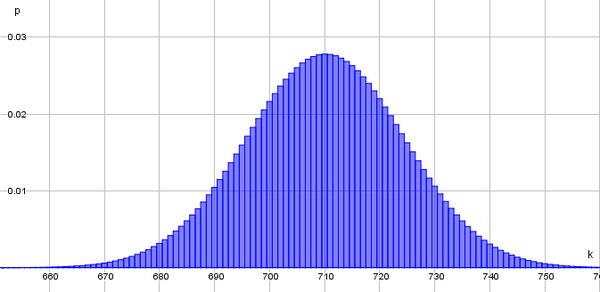

Überlege dir, welcher Rand der Binomialverteilung für die Partei interessant ist.
Dieser Rand ist dann der Verwerfungsbereich.

Der rotmarktierte Bereich ist der Verwerfungsbereich. Der Rest ist der Annahmebereich.

b) Schätze mit Hilfe der Binomialverteilung die Intervalle für den Annahme- und Verwerfungsbereich

Schaue dir dazu die Skizze bei a) an.

Der exakte Annahme- und Verwerfungsbereich lautet wie folgt: Annahmebereich {686, ..., 1000} und der Verwerfungsbereich {0,...685}.Wenn dein Werte in der Nähe liegen, ist es gut :) So kannst du immer beim späteren ausrechnen überprüfen, ob deine Werte Sinn ergeben.

c) Liegt das Umfrageergebnis im Verwerfungsbereich, wie kann die Partei dieses Ergebnis interpretieren?

Die Partei kann mit einer Irrtumswahrscheinlichkeit von 5% sagen, dass der Anteil der Menschen, die den Kimawandel als Bedrohung sehen im Vergleich zu 2019 gesunken ist.

d) Liegt das Umfrageergebnis im Annahmebereich, wie kann die Partei dieses Ergebis deuten?

Liegt das Ergebnis im Annahmebereich, so ist keine Aussage möglich.