Zufallsgrößen - Wahrscheinlichkeitsverteilungen - Erwartungswerte

Übergreifende Aufgabe

Erstelle auf Basis der Ergebnisse aller Aufgaben dieser Seite ein Produkt, aus dem die Bedeutung der eingeführten Fachbegriffe sowie die Vorgehensweise zur Berechnung neu eingeführter Werte hervorgeht. Entscheide selbst, in welcher Form du die Inhalte aufbereiten möchtest (z.B. in Textform, als Sketchnote, als Präsentation, ...)

Du darfst diese Aufgabe alleine oder in einer Gruppe von maximal vier Personen bearbeiten.

Grundlagen

Grundlagen

Im Erklärvideo werden wesentliche Grundbegriffe erklärt, die dir auf dieser Seite wieder begegnen werden. Sieh dir zuerst das Video an, bevor du weiter liest.

Video laden

Lokale Datei

Lokale Datei sammelt möglicherweise persönliche Daten.

FortfahrenAusblenden

Gewinnmöglichkeiten beim Glücksrad

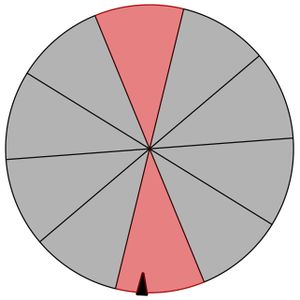
Klara bietet auf einem Straßenfest ein Glücksspiel an. Das abgebildete Glücksrad wird dreimal gedreht. Wird bei jeder Drehung ein graues Feld getroffen, so verliert man seinen Einsatz von 1,00 €. Wenn bei den drei Drehungen genau einmal ein rotes Feld getroffen wird, werden 1,50 € ausgezahlt, bei zweimal „rot” werden 2,50 € ausgezahlt und bei dreimal „rot” beträgt die Auszahlungssumme 5 €.

Die Wahrscheinlichkeiten der verschiedenen Gewinnsummen

Aufgabe 1

Stelle das dreimalige Drehen des Glücksrades in einem Baumdiagramm dar.

Aufgabe 2

Lege eine Tabelle an, in der du in der oberen Zeile die möglichen Gewinnsummen und darunter die Wahrscheinlichkeit, mit der die entsprechende Gewinnsumme erzielt wird, zusammenstellst. Du kannst dein Ergebnis überprüfen, indem du die Werte in die folgende Tabelle einträgst. Alle Werte, die nach einem Klick auf "Prüfen" stehen bleiben, sind korrekt.

Gewinnsumme:	-1,00|-1() €	0,50|0,5() €	1,50|1,5() €	4,00|4() €
Wahrscheinlichkeit:	0,512|64/125()	0,384|48/125()	0,096|12/125()	0,008|1/125()

Aufgabe 3

Stelle in deinem Ergebnis aus Aufgabe 2 einen Bezug zu den Begriffen Zufallsgröße und Wahrscheinlichkeitsverteilung her.

Welcher Gewinn ist zu erwarten?

Auf Basis der Wahrscheinlichkeitsverteilung der Gewinnsummen können wir nun herausfinden, mit welchem Gewinn jemand, der das Glücksspiel spielt, rechnen kann.

Aufgabe 4

Angenommen das Glücksspiel wird 1000-mal durchgeführt. Wie oft sind die verschiedenen Gewinnsummen dabei im Idealfall zu erwarten?

Berechne auf Basis der vorhergesagten absoluten Häufigkeiten das arithmetische Mittel der Gewinnsummen.

Nach dem Gesetz der großen Zahlen nähern sich die relativen Häufigkeiten der Ausgänge eines Glücksspiels bei sehr großer Versuchsanzahl immer weiter den theoretischen Wahrscheinlichkeiten an.

Nach 1000 Runden können als Schätzwert für die relativen Häufigkeiten der verschiedenen Gewinnsummen die Wahrscheinlichkeiten aus Aufgabe 2 verwendet werden. Berechne daraus die gesuchten absoluten Häufigkeiten.

Mit folgender Formel lässt sich das arithmetische Mittel berechnen:

$\bar x=\frac{1}{n}(x_1 \cdot H(x_1)+x_2 \cdot H(x_2)+ \cdots +x_{k-1} \cdot H(x_{k-1})+x_k \cdot H(x_k))$

Nach 1000 Versuchen hat man im Schnitt ein Gewinn von rund -0,14 € (genauer Wert: -0,144 €) - also ein Verlust von 0,14 € - gemacht.

Aufgabe 5

Berechne nun den Erwartungswert der Gewinnsumme mithilfe deiner Ergebnisse aus Aufgabe 2 und der Informationen aus dem Video. Sieh dir ggf. den Ausschnitt zum Erwartungswert noch einmal an. Was fällt auf?

Artihmetisches Mittel vs. Erwartungswert

Arithmetisches Mittel $\bar x$	Erwartungswert $\mu$ bzw. $E(X)$
beschreibt den Durchschnittswert eines vorhandenen Datensatzes basiert auf bereits vorliegenden Häufigkeiten Im Beispiel mit dem Glücksrad muss das Spiel zunächst mehrmals durchgeführt werden, damit auf Basis der bekannten Ausgänge das arithmetische Mittel der tatsächlichen Gewinnsummen berechnet werden kann.	beschreibt den zu erwartenden durchschnittlichen Wert, den die Zufallsgröße $X$ voraussichtlich annehmen wird basiert auf der Wahrscheinlichkeitsverteilung der Zufallsgröße $X$ Im Beispiel mit dem Glücksrad beschreibt der Erwartungswert durchschnittlich zu erwartenden Gewinn der Spieler und ist unabhängig vom tatsächlichen Ausgang des Spiels.

Handelt es sich um ein faieres Spiel?

Aufgabe 6

Formuliere Bedingungen, unter denen du ein Glücksspiel als fair bezeichnen würdest.

In der Stochastik liefert uns der Erwartungswert eine Möglichkeit, die Fairness eines Spiels zu beurteilen. Die Zufallsgröße $X$ soll weiterhin den Gewinn beschreiben.

Aufgabe 7

Was muss für den Erwartungswert $E(x)$ gelten, damit das Spiel sowohl aus Sicht des Spielers als auch aus Klaras Sicht als fair bezeichnet werden kann? Überlege zunächst selbst, recherchiere anschließend!

Entscheide auf Basis dieser Bedingung, ob Klaras Glücksspiel fair ist.

Überprüfe deine Einschätzung:

Ist das Spiel fair? (!Ja) (!Nein, Klara wird benachteiligt.) (Nein, der Spieler wird benachteiligt.)

Die Auszahlungssummen werden verändert.

Klara passt die Auszahlungsbeträge folgendermaßen an: Bei dreimal „grau” ist der Einsatz von einem € verloren, bei einmal „rot” werden 1,50 € ausgezahlt, bei zweimal „rot” werden 4 € ausgezahlt und bei dreimal „rot” beträgt die Auszahlungssumme 10 €.

Aufgabe 8

Stelle eine Wahrscheinlichkeitsverteilung für die Zufallsgröße $Y$, durch die die neuen Gewinnbeträge beschrieben werden, auf und berechne den Erwartungswert.

Überprüfe deine Ergebnisse:

Gewinnsumme:	-1,00|-1() €	0,50|0,5() €	3,00|3() €	9,00|9() €
Wahrscheinlichkeit:	0,512|64/125()	0,384|48/125()	0,096|12/125()	0,008|1/125()

$E(Y)=$ 0,04() €

Aufgabe 9

Berechne den Einsatz, den Klara verlangen müsste, damit es sich mit den neuen Auszahlungssummen um ein faires Spiel handelt.

Der Einsatz muss genau so groß sein, wie die durchschnittlich zu erwartende Auszahlungssumme.

Berechne den Erwartungswert der Zufallsgröße $Z$, die statt des Gewinns die Auszahlungssumme beschreibt.

Der Einsatz muss 1,04 € betragen.

Baumdiagramme und Pfadregeln

Vierfeldertafeln und bedingte Wahrscheinlichkeiten