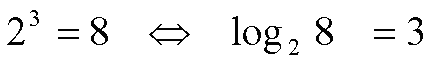Java/Sortieren
Um 10 v. Chr. ordnete Marcus Verrius Flaccus als Erster ein lateinisches Wörterbuch alphabetisch an. Die Menschen wollten schon immer wissen, wer der größte, stärkste, mächtigste ist. In unserem Zeitalter gilt um so mehr: Was sollte man mit einem ungeordneten Telefonbuch anfangen? Was nutzt eine Kunden- (aktuell eine Spender-) datei, die man nicht nach Namen, Alter, Wohnort, Einkommen sortieren kann?
Einführung von (statischen) Methoden
Oft gibt es in einem Computerprogramm Abläufe von Operationen, die mehrfach aufgerufen werden; das Sortieren ist dafür ein wichtiges Beispiel. Da man solche Handlungsanweisungen nicht immer wieder editieren möchte, modularisiert und verallgemeinert man diese Befehlsfolgen und nennt dies in Java eine Methode (in Pascal eine Funktion oder Prozedur). Insbesondere erreicht man durch den Aufruf von Modulen eine größere Übersichtlichkeit in der Aufrufebene.
Im letzten Kapitel (Mustererkennung) hätte man z.B. Methoden nutzen können, um die Felder mit Zufallszahlen zu füllen oder um die Inhalte aller Feldelemente auszugeben. Einer Methode kann man beim Aufruf Übergabe-Parameter mitschicken; man kann auch Werte zurück erhalten. Soll die Methode der ganzen Klasse zur Verfügung stehen (unabhängig von der Erzeugung eines Objektes), erhält die Methode den Modifier static.
Suche des Maximums in einem gegebenen Feld
Eine wichtige Vorstufe beim Sortieren ist das Finden eines Maximums z.B. in einem Zahlenfeld; dazu nutzen wir die Methode maximum und schicken das Feld a mit Typangabe als Parameter mit. Das int vor dem Methodennamen steht für den Rückgabetyp; unbedingt ist dann ein Ergebnis rückzumelden, und dies wird mit return gekennzeichnet.
public class Max {
static int maximum(int[] a) {
int n = a.length;
int max = a[0];
for (int i = 1;i < n;i++)
if (a[i] > max)
max = a[i];
return max;
}
public static void main(String[] args) {
int[] f = new int[] {9, 37,51,2,8,73,3,103,13,5,21};
int max = maximum(f);
System.out.printf("Das Maximum ist %d%n",max);
}
}
Ausgabe:
Das Maximum ist 103
In diesem Beispiel haben wir die Belegung des Feldes f gleich bei der Objekterzeugung von f als sog. Arrayliteral angegeben; interessanter ist es natürlich, das Feld zur Laufzeit z.B. durch einen Zufallsgenerator zu füllen. Außerdem wollen wir das Feld auch ausgeben.
Natürlich werden wir auch dafür statische Methoden einsetzen:
Methoden auch für Ein- und Ausgabe
import java.util.Scanner;
public class Max1 {
static int feld_laenge() {
Scanner s = new Scanner (System.in);
int n;
//Eingabeschleife bis sinnvolle Feldlänge
do {
System.out.println("Welche Feldlänge?");
n = s.nextInt();
}
while (n < 1);
return n;
}
static void feldein(int[] a) {
//Feldeingabemodul
for (int i = 0; i < a.length; i++)
a[i] = (int) Math.floor(Math.random()*10);
}
static void feldaus (int[] a) {
//Feldausgabemodul
System.out.printf("Ausgabe des Feldes:%n");
for (int i = 0; i < a.length; i++)
System.out.printf("%3d",a[i]);
System.out.printf("%n%n");
}
static int maximum(int[] a) {
// Bestimmung des Maximums
int n = a.length;
int max = a[n - 1];
for (int i = n - 2;i >= 0;i--)
if (a[i] > max)
max = a[i];
return max;
}
// Hauptprogramm
public static void main(String[] args) {
int[] f = new int[feld_laenge()];
feldein(f);
feldaus(f);
System.out.printf("Das Maximum ist %d%n",maximum(f));
}
}
Beispielausgabe:
Welche Feldlänge?
8
Ausgabe des Feldes:
3 2 0 5 0 2 6 5
Das Maximum ist 6
Auch hier erhalten die Methoden zur Ein- und Ausgabe einen Parameter (das Feld); eine Rückgabe ist jeweils nicht nötig, da der Feldübergabeparameter und die Feldvariable letztlich auf den gleichen Speicherplatz referenzieren (in den nächsten Kapiteln werden wir darlegen, dass Gleichsetzen von Objekten immer die Zuweisung des gleichen Speicherplatzes bedeutet). Methoden ohne Rückgabe erhalten den Modifier void. Außerdem ist zu beobachten, dass die Methode zur Eingabe der Feldlänge keinen Übergabeparameter hat (zu Methoden gehören aber immer - u.U. offene - Klammern) . Hier ist eine Rückgabe vorgesehen, und deshalb erzwingt der Compiler das return. Bemerkenswert ist, dass in Java die Feldlänge auch noch zur Laufzeit bestimmt werden kann!
Nochmals sei darauf hingewiesen, dass durch den Aufruf der Methoden der "rote Faden" im Hauptprogramm viel deutlicher erkennbar ist; die main-Methode hat an Übersichtlichkeit gewonnen.
Sortieren eines Feldes
Aus der Maximumsbestimmung lässt sich sehr konsequent Straight Selection als eines der drei elementaren Sortierverfahren ableiten; mehr darüber in den Erläuterungen zum Sortieren und in Algorithmen / Methoden und Aufwand.
import java.util.Scanner;
public class Sort{
static int feld_laenge() {
Scanner s = new Scanner (System.in);
int n;
do {
System.out.println("Welche Feldlänge n? (ganze Zahl ab 1)");
if (s.hasNextInt())
n = s.nextInt();
else {s.nextLine();
n = 0;} //Damit Eingabeschleife weiter läuft
}
while (n < 1) ;
return n;
}
//Die bereits bekannten Methoden sind wieder klein gedruckt
static void feldein(int[] a) {
//Feldeingabemodul
for (int i = 0; i < a.length; i++)
a[i] = (int) Math.floor(Math.random()*10);
}
static void feldaus (int[] a) {
//Feldausgabemodul
for (int i = 0; i < a.length; i++)
System.out.printf("%3d",a[i]);
System.out.printf("%n%n");
}
static void max_sort(int[] c) {
//Sortieren mit straight selection
int max;
int pos;
int n = c.length;
for (int i = n - 1; i > 0; i--) {
//Maximum für einen Schleifendurchgang
max = c[i];
// Position, an der man das Maximum findet
pos = i;
// ob man noch ein besseres Maximum für diesen Schleifendurchgang findet?
for (int j = i - 1 ; j >= 0; j--)
if (c[j] > max) {
max = c[j];
pos = j;
}
// Der alte Wert für das Maximum kommt an die Stelle, an der man den
// richtigen Wert fand
c[pos] = c[i];
c[i] = max;
}
}
public static void main(String[] args) {
int[] f = new int[feld_laenge()];
feldein(f);
System.out.printf("Ausgabe des Feldes vor dem Sortieren:%n");
feldaus(f);
max_sort(f);
System.out.printf("Ausgabe des Feldes nach dem Sortieren:%n");
feldaus(f);
}
}
Beispielausgabe:
Welche Feldlänge n? (ganze Zahl ab 1)
10
Ausgabe des Feldes vor dem Sortieren:
4 1 2 5 7 0 9 5 4 2
Ausgabe des Feldes nach dem Sortieren:
0 1 2 2 4 4 5 5 7 9
Mit diesem Programmbeispiel soll wieder gezeigt werden, wie man durch Modularisierung die Überschaubarkeit des Programmes optimieren und vom Hauptprogramm ausgehend die Intentionen nachvollziehen kann.
Ein weiteres wichtiges Thema ist die Robustheit der Benutzerschnittstelle und damit der Eingabemethode am Anfang: Diese muss fehlertolerant programmiert werden, d.h. das System darf nicht abstürzen, wenn Größenbereich oder Typ der Eingabedaten falsch gewählt sind.
Sehr gut lassen sich dazu Eingabeschleifen handhaben, welche solange laufen bis die Eingaben ok sind.
Dazu muss man wissen, dass der Scanner die Eingaben zunächst als Zeichenkette übernimmt, mit s.hasNextInt()prüft, ob der String in eine ganze Zahl umgewandelt werden kann und dies dann ggf. mit s.nextInt() realisiert. Im ungünstigen Fall muss mit s.nextLine() ein neuer String angefordert werden (hier wird außerdem noch der verbotene Wert 0 gesetzt; der Compiler achtet nämlich genau darauf, dass die Rückgabevariable der Methode wenigstens initialisiert ist).
Mischen zweier sortierter Felder
Elementare Sortierverfahren lassen sich anschaulich beschreiben; für die praktische Anwendung ist ihr quadratischer Aufwand jedoch nicht vertretbar; Ziel der weiteren Überlegungen wird also sein, den Aufwand deutlich zu reduzieren:
In einem ersten Schritt werden wir in diesem Abschnitt zwei sortierte Felder zu einem sortierten Feld mischen.
Im Sinne von "teile und herrsche" werden wir später ein Feld in zwei Felder teilen, jeweils sortieren und dann mischen.
In einem rekursiver Ansatz werden wir schließlich "teile und herrsche" "auf die Spitze treiben" und den Aufwand zwar nicht linear, aber immerhin linear - logarithmisch einstellen.
Für das Mischen übertragen wir folgenden Algorithmus:
Gegeben zwei sortierte Felder a und b mit den Längen n und m.
Erzeuge ein drittes Feld c (Feldplätze vom gleichen Datentyp) der Länge n + m.
Vergleiche die Feldplätze von a und b und schreibe das kleinere Feldelement auf den nächsten Feldplatz von c. Falls das letzte Feldelement noch nicht erreicht ist, erhöhe den Feldindex in dem Feld, in dem das kleinere Feldelement gefunden wurde; ansonsten übertrage künftig (schrittweise und ohne Vergleich) die übrigen Werte des anderen Feldes nach c.
import java.util.Scanner;
public class Mischen {
// Hier erhält auch eine Variable den Modifier static;
// dadurch steht der Scanner in allen Methoden zur Verfügung
static Scanner s = new Scanner (System.in);
// Welche Länge soll ein Feld haben?
static int feld_laenge(int ug,int og) {
// Untere und obere Grenze als Übergabeparameter
int n;
// Eingabeschleife
do {
System.out.printf(" Ganze Zahl ab %d bis %d%n",ug,og);
if (s.hasNextInt())
n = s.nextInt();
else {s.nextLine();
n = ug - 1;} //Damit Eingabeschleife weiter läuft
}
while ((n < ug) ||(n > og)) ;
return n;
}
//Die bereits bekannten Methoden sind wieder klein gedruckt
static void feld_ein(int[] c) {
//Feldeingabemodul
for (int i = 0; i < c.length; i++)
c[i] = (int) Math.floor(Math.random()*10);
}
static void feld_aus(int[] c) {
// Feldausgabemodul
System.out.println();
for(int i = 0; i <c.length; i++)
System.out.printf("%3d,",c[i]);
}
static void max_sort(int[] c) {
//Sortieren mit straight selection
int max;
int pos;
int n = c.length;
for (int i = n - 1; i > 0; i--) {
max = c[i];
pos = i;
for (int j = i - 1 ; j >= 0; j--)
if (c[j] > max) {
max = c[j];
pos = j;
}
c[pos] = c[i];
c[i] = max;
}
}
static int [] mischen (int[]a, int[] b ) {
//sortierte Felder mischen,indem man jeweils die Feldelemente vergleicht
// und das kleinere in einem dritten Feld notiert.
// Feldlängen
int n = a.length;
int m = b.length;
// neues Feld erzeugen
int[] c = new int[n + m];
int i = 0;
int j = 0;
int k = 0;
// Jeweils prüfen, welches Feldelement in c kommt
// Aufhören, wenn ein Feld alle Werte eingefügt hat;
// Dann muss man später nur noch mit dem anderen Feld auffüllen
while ((k < n + m) && (i != n) && (j != m)) {
if (a[i] <= b[j]) {
c[k] = a[i];
i++;
}
else {
c[k] = b[j];
j++;
}
k++;
}
// Wenn aus a schon alle Werte eingefügt sind, muss man nur noch die Werte
// aus b auffüllen; etc.
// Die Werte der Laufvariablen k, i und j werden aus der While-Schleife
//übernommen.
if (i == n )
for (int l = k ; l < (n + m); l++) {
c[l] = b[j];
j++;}
else
for (int l = k ; l < (n + m); l++) {
c[l] = a[i];
i++;}
return c;
}
public static void main (String[] args) {
// Laenge der Felder erfragen
System.out.printf("Wie lange ist das erste Feld? (höchstens 20) %n");
int n = feld_laenge(1,20);
System.out.printf("Wie lange ist das zweite Feld? (höchstens 20) %n");
int m = feld_laenge(1,20);
// 2 Felder einrichten, einlesen und sortieren
int[] a = new int[n];
int[] b = new int[m];
feld_ein(a);
feld_ein(b);
System.out.printf("%nDie beiden unsortierten Felder%n");
feld_aus(a);
feld_aus(b);
max_sort(a);
max_sort(b);
System.out.printf("%nDie beiden sortierten Felder%n");
feld_aus(a);
feld_aus(b);
int[] c = new int[n+m];
// Zwei sortierte Felder mischen
c = mischen(a,b);
System.out.printf("%nDas sortierte Feld nach dem Mischen%n");
feld_aus(c);
}
}
Beispielausgabe:
Wie lange ist das erste Feld? (höchstens 20) Ganze Zahl ab 1 bis 20 10 Wie lange ist das zweite Feld? (höchstens 20) Ganze Zahl ab 1 bis 20 3 Die beiden unsortierten Felder 5, 9, 4, 3, 8, 3, 7, 5, 1, 0, 0, 6, 6, Die beiden sortierten Felder 0, 1, 3, 3, 4, 5, 5, 7, 8, 9, 0, 6, 6, Das sortierte Feld nach dem Mischen 0, 0, 1, 3, 3, 4, 5, 5, 6, 6, 7, 8, 9,
Grundsätzlich wäre es sinnvoll gewesen, die Feldlängen n und m zu statischen Variablen zu erheben (vgl. Scannervariable s); man hätte sich dann erspart, in allen Methoden die Feldlänge neu zu bestimmen... Andererseits sollten zentrale Input- / Output - / Sortiermethoden leicht in andere Projekte portierbar und damit autonom sein. Die bisherigen Feldmethoden hatten alle den Modifier void. Eine Rückgabe war nicht erforderlich, da man in der Aufrufebene und auf Methodenebene immer das gleiche Feld-Objekt referenzierte; vgl. Die Methode Mischen allerdings gibt ein weiteres (sortiertes) Feld zurück; dieses muss vor dem Aufruf der Methode erzeugt werden.
Feld halbieren, sortieren und mischen
Wie oben schon angekündigt werden wir jetzt im Sinne von "divide and conquer" daran gehen, den Aufwand durch Halbieren des Feldes zu verringern: Der Aufwand lässt sich z.B. durch die Zahl der Vergleiche beschreiben; für diese Zahl kann man bei Straight Selection den Term
1/2*n*(n - 1)
elementar herleiten; halbe Feldlänge bedeutet also weniger als halb soviel Aufwand, so dass es sich also lohnt, Untersuchungen in dieser Richtung anzustellen.
Unser Verfahren wird also die beiden Feldhälften elementar sortieren und dann mischen. Diesmal lassen wir uns nicht die Felder, sondern die Zahl der notwendigen Vergleiche ausgeben. Dazu benötigen wir eine statische Variable v, die wir im Sortier- und Mischalgorithmus jeweils passend als Zähler einbauen.
Als Vergleichswert bei n = 100 Feldelementen (wenn man ausschließlich mit Straight Selection sortiert) ist nach obiger Formel 4950 anzusetzen. Diesen Wert gilt es zu unterbieten…:
import java.util.Scanner;
public class Halb_Sort {
static Scanner s = new Scanner (System.in);
// Zähler für Vergleiche
static int v= 0;
static void feld_ein(int[] c) {
//Feldeingabemodul
for (int i = 0; i < c.length; i++)
c[i] = (int) Math.floor(Math.random()*10);
}
static int feld_laenge(int ug) {
// Untere Grenze als Übergabeparameter
int n;
do {
System.out.printf(" Ganze Zahl ab %d %n",ug);
if (s.hasNextInt())
n = s.nextInt();
else {s.nextLine();n = ug - 1;}
}
while (n < ug);
return n;
}
static void max_sort(int[] c) {
//Sortieren mit straight selection
int max;
int pos;
int n = c.length;
for (int i = n - 1; i > 0; i--) {
max = c[i];
pos = i;
for (int j = i - 1 ; j >= 0; j--) {
v++;
if (c[j] > max) {
max = c[j];
pos = j;
}
}
c[pos] = c[i];
c[i] = max;
}
}
static int [] mischen (int[]a, int[] b ) {
//Wie oben; bis auf den Zähler v
int n = a.length;
int m = b.length;
int[] c = new int[n + m];
int i = 0;
int j = 0;
int k = 0;
while ((k < n + m) && (i != n) && (j != m)) {
if (a[i] <= b[j]) {
c[k] = a[i];
i++;
}
else {
c[k] = b[j];
j++;
}
k++;
v++;
}
if (i == n )
for (int l = k ; l < (n + m); l++) {
c[l] = b[j];
j++;}
else
for (int l = k ; l < (n + m); l++) {
c[l] = a[i];
i++;}
return c;
}
static int[] sort (int[] a) {
int n = a.length;
if (n > 1)
{
// Zwei neue Felder anlegen
int m = n / 2;
int []l =new int[m];
int []r =new int[n-m];
// Die zwei Hälften mit den passenden Feldelementen füllen
for (int i = 0; i < m; i++)
l[i] = a[i];
for (int i = 0; i < (n-m); i++)
r[i] = a[m +i];
// jede Hälfte sortieren
max_sort(l);
max_sort(r);
// Die beiden sortierten Hälften zusammenfügen
a = mischen(l,r);
}
return a;
}
public static void main(String[] args) {
System.out.printf("Wie lange soll das Feld sein? %n");
int n = feld_laenge(1);
// Feld einrichten und einlesen
int[] f = new int[n];
feld_ein(f);
// Sortieren
f = sort(f);
System.out.printf("%d Vergleiche", v);
}
}
Beispielausgabe:
Wie lange soll das Feld sein?
Ganze Zahl ab 1
100
2545 Vergleiche
Falls man sich die Mühe macht und das Feld sogar in vier Teile teilt, sortiert und mischt, schwankt die Zahl der Vergleiche sogar nur noch um 1380 (vgl. Quelltext Viertel_Sort.java). Insgesamt haben wir also unser Ziel erreicht, den Aufwand deutlich zu verringern; allerdings kann man leicht zeigen, dass sich die Zahl der wesentlichen Vergleiche immer noch mit dem Quadrat von n entwickelt. Außerdem war der Programmieraufwand für das Zerlegen des Feldes in 4 Teile bereits schon sehr groß (vgl. Quelltext Viertel_Sort.java). Ein Aufwand weniger als quadratisch wäre aber letztlich nur erreichbar, wenn wir das Feld so weit zerlegen, dass die Feldlänge jeweils 1 ist.... Dies soll im nächsten Abschnitt begründet werden.
Sortieren durch Mischen (Mergesort)
Es bietet sich also an, das gegebene Feld fortgesetzt zu halbieren, d.h. aus der Methode die Methode selbst aufzurufen: Das optimierte Sortierprogramm ist rekursiv zu formulieren und allgemein als Mergesort bekannt:
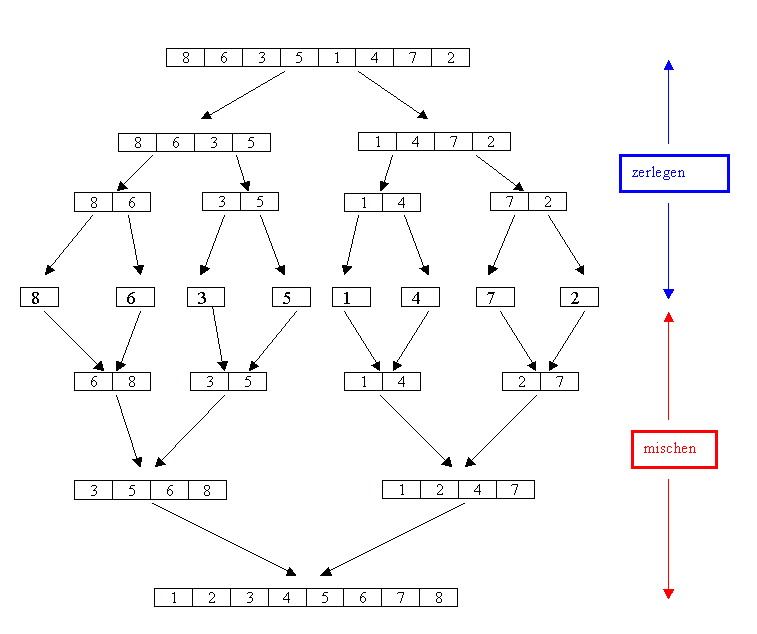
Wenn wir im folgenden Beispiel von n = 8 Feldelementen ausgehen, erreichen wir mit drei Halbierungsdurchgängen jeweils als Feldlänge 1. Die Drei ist der Schlüssel zur Lösung unseres Aufwandproblemes:
Entsprechend vollzieht sich auch das Mischen in drei Ebenen:
- In der ersten Stufe gibt es 4 = n / 2 Vergleiche.
- In der zweiten Stufe gibt es (mindestens) 2 * 2 = 4 Vergleiche.
- In der dritten Stufe gibt es (mindestens) 4 Vergleiche.
Insgesamt gibt es also 3 * 4 = log( 8) * 8 / 2 Vergleiche; damit ist die bekannte Beziehung für den Aufwand n * log (n) motiviert.
Um Mergesort zu realisieren, müssen wir im letzten Programm (Halb_Sort) nur die Methode sort() durch folgenden rekursiven Ansatz austauschen; alle anderen Methoden - auch das Mischen - sind bereits entwickelt! Die Methode max_sort (Straight Selection) entfällt naturgemäß ganz!
static int[] sort (int[] a) {
// Rekursionsende bei Feldlänge 1
int n = a.length;
if (n > 1)
{
// Zwei neue Felder anlegen
int m = n / 2;
int []l =new int[m];
int []r =new int[n-m];
// Die zwei Hälften mit den passenden Feldelementen füllen
for (int i = 0; i < m; i++)
l[i] = a[i];
for (int i = 0; i < (n-m); i++)
r[i] = a[m +i];
// jede Hälfte sortieren; rekursiver Aufruf!
l = sort(l);
r = sort(r);
// Die beiden sortierten Hälften zusammenfügen
a = mischen(l,r);
}
return a;
}
Wesentliche Vergleiche werden hier nur in der Mischenmethode gezählt: Beispielausgabe:
Wie lange soll das Feld sein?
100
530 Vergleiche
Mit 4950 Vergleichen bei 100 Feldelementen hatten wir bei Straight Selection begonnen, so dass wir am Schluss auch eine sehr schöne experimentelle Bestätigung der Theorie zur Aufwandsbetrachtung haben.