Chemie-Lexikon/Stöchiometrie - Einführung in die Stoffmenge und das Mol

Unsere bisherigen Berechnungen beruhten meist auf Massenverhältnissen, die wir anhand der ausgeglichenen Reaktionsgleichung bestimmen konnten. Damit haben wir für jede Art von Aufgaben eine Möglichkeit stöchiometrische Berechnungen durchzuführen.

Beim Satz von Avogadro haben wir aber sehen können, dass die Anzahl der Teilchen, die bei gasförmigen Stoffen miteinander reagieren, ausreicht, um Aussagen über die Volumina an Edukten und Produkten zu machen. Warum können wir nicht genauso bei Feststoffen oder Flüssigkeiten vorgehen? Hintergrund ist, dass die Teilchen bei gasförmigen Stoffen einen recht großen Abstand haben und dieser ist abhängig vom Stoff, dessen Teilchen und deren Interaktion, was ja überhaupt erst den Satz von Avogadro möglich macht. Bei Feststoffen und bei Flüssigkeiten sind die Teilchen aber eng beeinander. Hier sind es die Teilchen und deren Größe, die bestimmen, wieviele Teilchen auf eine Volumeneinheit kommen. Und da die Teilchen der verschiedenen Stoffe eine unterschiedliche Größe und Masse haben, können wir hier nicht vom Volumen ausgehen.

Die Geschichte des Mols

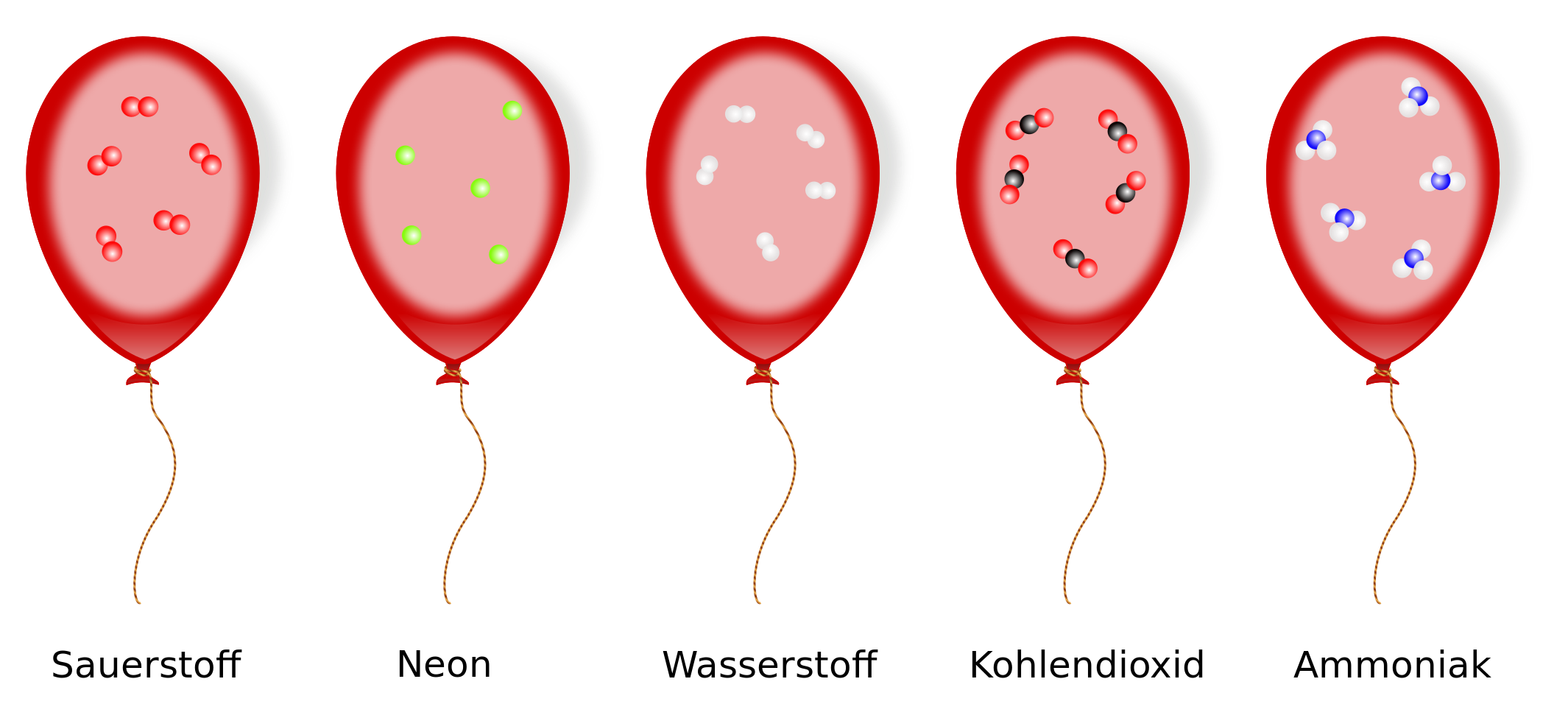
Beim Satz von Avogadro geht es vor allem um die Teilchenanzahl, die bei gleichem Volumen, gleichem Druck und Temperatur identisch ist. Wieviele Teilchen in einer Volumeneinheit tatsächlich enthalten sind, war zu Zeiten Avogadros (um 1811) noch gar nicht bekannt. Denn man konnte zwar bei vielen Atomen abschätzen, wie sich ihre Massen zueinander verhielten (die relative Atommasse!) , aber wie groß bzw. klein die Masse einzelner Atome im Vergleich zu messbaren Masseneinheiten wie dem Gramm war, konnte überhaupt nicht abgeschätzt werden. Auch die Größe der Atome selber war noch nicht bekannt.

Relative und Absolute Atommasse

• Die relative Atommasse, gibt die Massen einzelner Atome im Vergleich zu anderen Atomen an.

Die erste Tabelle mit relativen Atommassen wurde 1805 von John Dalton veröffentlicht. Er erhielt sie anhand der Massenverhältnisse bei chemischen Reaktionen, wobei er das leichteste Atom, das Wasserstoffatom, als „Masseneinheit“ wählte.

• Die absolute Atommasse wird in kg, g oder u angegeben und ist damit genau, über die Basiseinheit für die Masse definiert.

Tatsächlich wurde die Frage nach der wirklichen Masse oder Größe eines Atomes bis 1865 als eher unwichtig angesehen, denn man konnte sich nicht vorstellen, wie man eine solch kleine Masse oder Größe bestimmen sollte. Im Jahre 1865 dagegen wurde durch Überlegungen und Berechnungen des österreichischen Physikers und Chemikers Joseph Loschmidt erstmals möglich, die Zahl an Molekülen größenordnungsmäßig zu bestimmen, also abzuschätzen im Bereich welcher 10er-Potenz die Masse bzw. die Anzahl der Teilchen in einer Volumeneinheit liegen. So gab Loschmidt selber als die Größe für Luftteilchen an, dass sie etwa 1 Millionstel eines Millimeters als Durchmesser haben. Nach heutigen Erkenntnissen lag er damit etwa um den Faktor 3 daneben (die Teilchen sind 3-mal kleiner, als Loschmidt annahm), was er aber selber vorhersagte. Trotzdem ist die Genauigkeit erstaunlich. Aus diesen Werten konnte dann auch die Masse der Gasteilchen bestimmt werden und damit wurden aus den relativen Atommassen absolute Werte.

Für seine Überlegungen nutzte Loschmidt die kinetische Gastheorie, wo es um die Eigenschaften von Gasen geht, insbesondere die Gasgesetze, die auch Avogadro schon für seine Berechnungen genutzt hat. Dabei wird die Energie der Gasteilchen betrachtet, die Übertragung von Energie bei Kollisionen untereinander und mit anderen Objekten (wie die Außenwand eines Gefäßes), die den Gesetzen der allgemeinen Mechanik gehorchen mussten.

• 

  Amadeo Avogadro

• 

  Josef Loschmidt

• 

  Wilhelm Ostwaldt

Der Begriff „Mol“ wurde um 1900 von Wilhelm Ostwald geprägt und ist vermutlich von dem Begriff „Molekül“ abgeleitet. 1911 wurde die Avogadro-Konstante oder auch Loschmidtsche Zahl als die Anzahl der Teilchen pro Mol eines Stoffes eingeführt. Im Jahr 1971 wurde das Mol als Basiseinheit in das Internationale Einheitensystem oder SI aufgenommen als eine Einheit, mit der die Stoffmenge bzw. Teilchenanzahl bestimmt wird.

Die SI-Einheiten

Das Internationale Einheitensystem oder SI (frz. Système international d’unités) ist das am weitesten verbreitete Einheitensystem für physikalische Größen. Es ist dezimal (d. h. die Bruchteile oder Vielfachen der einzelnen Basiseinheiten unterscheiden sich nur um Zehnerpotenzen) und wird weltweit genutzt. Im Gegensatz dazu sind in vielen englisch-sprachigen Ländern und diejenigen des britischen Commonwealth die Maßeinheiten der imperial units immer noch weit verbreitet, die immer unterschiedliche Umrechnungszahlen haben (wie etwa Yard, Meile, Unze, Pfund, Pint, ...) - mehr dazu unter Angloamerikanisches Maßsystem

Größe	Länge	Masse	Zeit	Stromstärke	Temperatur	Stoffmenge	Lichtstärke
Einheit	Meter $m$	Kilogramm $kg$	Sekunde $s$	Ampere $A$	Kelvin $K$	Mol $mol$	Candela $cd$

Die Größen werden dabei meist durch Naturkonstanten definiert, die unabhängig von Zeit und Ort sind.

Das Mol und die Stoffmenge

• Ein Mol ($n = 1 mol$) enthält etwa 6,022 · 10²³ Teilchen. Diese Zahl ist so definiert, dass 12 g Kohlenstoff des Isotops C-12 genau einem Mol entsprechen.
  • Die Avogadro-Konstante $N_A$ ist festgelegt als die Anzahl der Teilchen pro Mol . Damit ist $N_\mathrm{A} = 6,022\;140\;857\;(74) \cdot 10^{23}\ \mathrm{mol}^{-1}$, wobei die Einheit Teilchen pro Mol bedeutet.
• Die Stoffmenge (Symbol $n$) gibt indirekt die Teilchenzahl einer Stoffportion an. Teilchen können hier Atome, Ionen, Moleküle, Formeleinheiten oder auch Elektronen sein.

Zum besseren Verständnis, was $n = 1 mol$ bedeutet oder wie es verwendet werden kann, passt der Vergleich dem "Dutzend", wobei 1 Dutzend eine Stückzahl von zwölf bezeichnet. So sind 2 Dutzend Eier dann $2\;Dutzend = 2 \cdot 12\;Stueck = 24\;Stueck$ oder $\frac{1}{2}\;Dutzend = 0.5 \cdot 12\;Stueck = 6 \;Stueck$.

Bei Mol ist es ähnlich: 1 mol entspricht 6,022 · 10²³ Teilchen und damit sind 2 mol Teilchen, dann also $2 \;mol = 2 \cdot 6,022 \cdot 10^{23} Teilchen = 12,044 \cdot 10^{23} \;Teilchen$ oder $0,5 \;mol = 0,5 \cdot 6,022 \cdot 10^{23}\; Teilchen = 3,011 \cdot 10^{23} \;Teilchen$

AUFGABE 1 - Hast du das "Mol" verstanden?

Bearbeite → dieses Quiz, um zu testen, ob die Begriff und die Defintion von Mol und Stoffmenge verstanden hast!

WICHTIG: Halte dir bei Fehlern, die du gemacht hast, die Frage fest und die richtige Antwort, nachdem du sie gefunden hast. Versuche eine Erklärung dafür zu finden, warum "diese" Antwort richtig ist. Dies wird im Unterricht gemeinsam besprochen!

Die Bedeutung des Mol für Reaktionen

Mit dem Mol, als Anzahl für die Teilchen, hat man nun die Möglichkeiten, die Mengen der beteiligten Stoffe statt in einer Masseneinheit wie Gramm oder Kilogramm auch in Mol anzugeben.

Beispiel: Die Reaktion von Lithium mit Wasser

$2 \, Li + 2 \, H_2O \rightarrow 1 \, H_2 + 2 \, LiOH$

Bei der Bildung von LiOH reagieren nach der Reaktionsgleichung zwei Lithium-Atome mit zwei Wassermolekülen zu einem Wasserstoffmolekül und 2 Einheiten Lithiumhydroxid. Weil in einem Mol von jeder Substanz gleich viele Teilchen vorhanden sind, kann man dann auch sagen, dass 2 mol Lithium-Atome mit 2 mol Wasser zu 1 mol Wasserstoff und 2 mol Lithiumhydroxid reagieren. Da bei den meisten Stoffen die Art der kleinsten Teilchen klar festgelegt sind, muss man auch nicht angeben, um welche Art von Teilchen es geht.

Damit kann man aus der Reaktionsgleichung, ähnlich wie beim Satz von Avogadro, schnell Angaben zu Stoffmengen-Verhältnissen bei Reaktionen angeben. Und das unabhängig davon, ob es ein gasförmiger, flüssiger oder fester Stoff ist.

AUFGABE 2 - Stoffmengenverhältnisse bei Reaktionen angeben.

Versuche, ob die du die Fragen zu den Stoffmengenverhältnissen in → diesem Quiz beantworten kannst.

Denk daran, dass es um Verhältnisse geht, die sich anhand der stöchiometrischen Koeffizienten aus den Reaktionsgleichungen ergeben.

Problematisch ist, dass man ein Mol Teilchen nicht so einfach abzählen kann. Daher müssen wir noch weitere Begriffe einführen, damit die Stoffmenge sinnvoll nutzbar ist.

Die Molmasse

Warum hat man eigentlich das Mol auf eine Anzahl von etwa 6,022 · 10²³ Teilchen festgelegt? Eventuell wäre doch eine glatte Zahl praktischer?

Die Anzahl von etwa 6,022 · 10²³, also der Avogadro-Konstante $N_A$, ergibt sich aus dem Wunsch, die Anzahl der Teilchen und damit die Stoffmenge möglichst einfach zu bestimmen. Das Besondere an der Zahl ist, dass sie dem Umrechnungsfaktor von der Atomaren-Masseneinheit u in die Massen-Einheit g entspricht.

ZUR ERINNERUNG Umrechnung von u zu g

$1 \;u = 1,660539040 \cdot 10^{-24} g$ bzw. $1 \;g = 6,02214085774 \cdot 10^{23} u$

Dies ist in der Definition von 1 mol enthalten, denn da heißt es:

12 g Kohlenstoff des Isotops C-12 entsprechen genau einem Mol.

Da das C-12 Isotop die Masse von etwa 12 u hat, könnte man die Masse von einem Mol C-12 Isotopen berechnen, wenn man den rechnerischen Zusammenhang zwischen g und u nutzt:

$m(1 \; mol \; C^{12})$

$\; = 6,02214085774 \cdot 10^{23} \cdot m(C^{12})$

$\; = 6,02214085774 \cdot 10^{23} \cdot 12 u$

$\; = 6,02214085774 \cdot 10^{23} \cdot 12 \cdot 1,660539040 \cdot 10^{-24} g$

$\; = 6,02214085774 \cdot 10^{23} \cdot 1,660539040 \cdot 10^{-24} \cdot 12 g$

$\; = 1 \cdot 12 g$

$\; = 12 g$

Die Masse von einem Mol C-12 Isotope kann aus der Anzahl der Teilchen (Avogadro-Konstante $N_A$) pro Mol bestimmt werden, indem man die Masse von einem C-12-Isotop nimmt, die 12 u ist. Dann wird die Umrechnungszahl von u in g genutzt, um den (noch nicht ausgerechneten) Wert der Masse in g umzurechnen. Die Zahl der Avogadro-Konstante und der Umrechnungsfaktor heben sich zu 1 auf und daher hat ein Mol von C-12-Isotopen die Masse von 12 g.

Diese Vorgehensweise ist natürlich etwas umständlich, wenn man mit Stoffmengen bei Reaktionen arbeiten will. Wichtig wäre es auch umgekehrt zu wissen, wieviel mol einer gegebenen Stoffportion entsprechen, also quasi, wieviele Teilchen in einer abgewogenen Menge eines Stoffes enthalten sind.

Was wir wissen ist, das man aufgrund des Zusammenhangs zwischen Avogadro-Kontante und Umrechnungsfaktor von u in g die Masse von einem Mol sehr einfach bestimmen kann.

BEGRIFF Molmasse

Die Masse von 1 mol eines Stoffes (= Molmasse) kann aus der Masse des Teilchens bestimmt werden. Die Einheit ist $\frac{g}{mol}$ also Gramm pro Mol, als Symbol verwendet man M.

Beispiele:

• Lithium besteht aus Atomen, die jeweils die Masse 6,94 u haben. 1 mol Lithium(-Atome) hat dann die Masse M = 6,94 g/mol.
• Wasser besteht aus H₂O-Molekülen, wobei jedes Wasser-Molekül die Masse 18 u hat. 1 mol Wasser hat dann die Masse 18 g und die Molmasse ist M = 18 g/mol.

Wieviel Mol Schwefel ist das wohl?

Bevor es an Berechnungen bei Reaktionsgleichungen geht, solltest du erst einmal ein wenig die Berechnung der Molmasse üben.

AUFGABE 3 - Bestimme Molmassen (1)

Bestimme die Molmassen für die folgenden Stoffe:

$H_2O$ , $3 \ CO$ , $Na_2SO_3$ , $2 H_2S$ , $Ca(HSO_4)_2$

LÖSUNG - Aufgabe 3

Die stöchiometrischen Faktoren muss man hier ignorieren, da es um die Stoffe und damit die vorhandenen Teilchen geht. Denn die Molare Masse ist eine Stoffeigenschaft.

$M(H_2O)=18 \frac{g}{mol}$ , $M(CO) = 28 \frac{g}{mol}$ , $M(Na_2SO_3) = 126 \frac{g}{mol}$ , $M(H_2S)=34,1\frac{g}{mol}$ , $M(Ca(HSO_4)_2) = 234 \frac{g}{mol}$

AUFGABE 4 - Bestimme Molmassen (2)

Bei dieser Aufgabe musst du erst das Teilchen des Stoffes bestimmen, für das du die Molmasse bestimmen sollst.

Wasserstoff, Methan, Kochsalz, Gold, Kohlendioxid, Chlor, Dialuminiumtrioxid, Ammoniak

LÖSUNG - Aufgabe 4

ACHTUNG: Denke an die Chlorreichen Sieben!

Wasserstoff $M(H_2)=2 \frac{g}{mol}$, Methan $M(CH_4)=16,4 \frac{g}{mol}$ , Kochsalz $M(NaCl)=58,44 \frac{g}{mol}$, Gold $M(Au)=197 \frac{g}{mol}$, Kohlendixod $M(CO_2)=44,01 \frac{g}{mol}$; Chlor $M(Cl_2)=70,9 \frac{g}{mol}$, Dialuminiumtrioxid $M(Al_2O_3)=101,96 \frac{g}{mol}$, Ammoniak $M(NH_3)=17,03 \frac{g}{mol}$

Berechnungen mit der Molmasse

Da wir nun wissen, wie wir mit Hilfe der Summenformel eines Stoffes und dem Periodensystem bestimmen können, wieviel 1 mol eines Stoffes wiegt, können wir das nun weiter nutzen, um von einer beliebigen Portion, dessen Masse wir kennen, die Stoffmenge zu bestimmen.

IDEE Zählen durch Wiegen

Nehmen wir mal an, du hast einen ganzen Haufen von cent-Stücken gesammelt. Hast du Lust, sie zu zählen? Vermutlich nein, aber das ist auch gar nicht notwendig, denn es gibt einen recht einfachen Trick, wenn du eine Waage zur Hand hast:

• 

  Das Masse von einer 10-Cent Münze kann man leicht bestimmen. Wenn man diese Masse kennt ...

• 

  ... kann man durch das Wiegen des gesamten Haufens und Teilen durch die Masse von einer Münze, die Anzahl im Haufen bestimmen.

Allgemein ist die Rechnung:

$Anzahl = \frac{Masse\;Haufen}{Masse\;einer\;Muenze}$

Dieses Prinzip können wir auch bei der Berechnung der Stoffmenge anwenden, indem wir die Molmasse nutzen. Dann könnte man zum Beispiel aus Reaktionsgleichungen nicht nur erkennen, welche Stoffmengen da miteinander reagieren, sondern auch Massen bestimmen.

Wenn wir uns an die Reaktionsgleichung der Thermit-Reaktion anschauen ...

$Fe_2O_3 + 2 Al \longrightarrow 2 Fe + Al_2O_3$

... dann ist ja erkennbar, dass 1 mol Eisenoxid $Fe_2O_3$ mit 2 mol Aluminium $Al$ reagieren. Oder es würden auch 2 mol Eisenoxid mit 4 mol Aluminium reagieren. Gehen wir zum Beispiel wieder von den 35 g Eisenoxid aus, dann könnten wir berechnen, wieviel Mol das sind.

Wenn wir nun berechnen könnten, wieviel Mol eine bestimmte Portion eines Stoffes (gewogen, also z.B. in g oder kg) ist, dann könnte man aus dem bekannten Stoffmengenverhältnis bestimmen, wieviel Mol des gesuchten Stoffes entsteht.

Berechnung der Stoffmenge

WICHTIG Berechnung der Stoffmenge

Die Stoffmenge n einer Stoffportion lässt sich bestimmen, indem man die Masse m einer Stoffportion durch die Molmasse M des Stoffes teilt.

Als Formel:

$n = \frac{m}{M}$ oder $Stoffmenge = \frac{Masse}{Molmasse}$

Beispiel:

Eine Portion Schwefel wiegt 23,5 g, also ist $m(S)\;=\;23,5\; g$. Die Molmasse von Schwefel ist $M(S)\;= \;32,06 \;g/mol$. Daraus kann die Stoffmenge der gegebenen Portion Schwefel bestimmt werden durch die Rechnung:

$n(S) = \frac{m(S)}{M(S)}=\frac{23,5 g}{32,06 g/mol} \approx 0,733 mol$

Hinweis: Die Einheit g wird bei der Rechnung weggekürzt, so dass nur "mol" übrig bleibt!

So können wir also berechnen, welche Stoffmenge, also mol, 35 g Eisenoxid sind?

Gegeben ist m(Fe₂O₃) = 35 g. Wegen der Molmasse M(Fe₂O₃) = 159,7 g/mol ergibt sich für die Stoffmenge n = 0,22 mol.

Und nun erst einmal, ein paar Übungen dazu.

AUFGABE 5 - Bestimme die Stoffmengen

WICHTIG: Denk daran, dass du bei allen Aufgaben die Molmasse der betrachteten Stoffes zuerst berechnen musst! Wenn ein Volumen gegeben ist, musst du vorher noch mit der Dichte die Masse bestimmen.

$50 g \ Fe_2O_3$, $123 g \ AlCl_3$, $10 g \ Wasserstoff$, $2,5 l \ Wasser$, $1 kg \ Helium$, $165,3 g \ Magnesiumoxid$, $10 l \ Sauerstoff$

LÖSUNG - Aufgabe 5

Wasserstoff

• $50 g \ Fe_2O_3$: $M(Fe_2O_3)=160 \frac{g}{mol}$, $n = 0,31 mol$
• $123 g \ AlCl_3$: $M(AlCl_3)=133,5 \frac{g}{mol}$, $n = 0,92 mol$
• $10 g \ Wasserstoff$: $M(H_2)=2 \frac{g}{mol}$, $n = 5 mol$
• $2,5 l \ Wasser = 2500 g Wasser$: $M(H_20)=18 \frac{g}{mol}$, $n = 138,98 mol$
• $1 kg \ Helium$: $M(He)=4 \frac{g}{mol}$, $n = 250 mol$
• $165,3 \ MgO$: $M(MgO)=40,3 \frac{g}{mol}$, $n = 4,1 mol$
• $10 l \ Sauerstoff$: aus der Tabelle im Buch $\rho(Sauerstoff)=1,43 \frac{g}{l}$, dadurch ergibt sich $m(O_2)= 14,29 \ g$, $M(O_2) = 32 \frac{g}{mol}$, $n = 0,45 mol$

TIPP Ausführliches Aufschreiben

Wenn du mit mehreren Werten und Stoffen rechnen musst, ist es sinnvoll, die Informationen ausführlich aufzuschreiben, also $M(S) = ...$, $m(S) = ...$ und $n(S) = ...$, damit man die Werte nicht durcheinander bringt

Nun hatten wir ja bestimmt, wieviel mol die 35 g Fe₂O₃ sind, nämlich 0,22 mol. Da 1 mol Eisenoxid $Fe_2O_3$ mit 2 mol Aluminium $Al$ reagieren, also die doppelte Menge Aluminium gebraucht wird, bräuchte ich zu den 35 g Eisenoxid also das doppelte von 0,22 mol, also 0,44 mol Aluminium. Nun muss man nur noch bestimmen, wieviel die 0,44 mol Aluminium wiegen.

Berechnungen der Masse

Mit Hilfe der Formel zur Berechnung der Stoffmenge kann man auch umgekehrt bestimmen, wieviel eine bestimmte Stoffmenge wiegt. Dazu muss man nur die Formel umstellen!

WICHTIG Bestimmung der Masse einer Stoffportion

Umformung nach $m$

$n = \frac{m}{M} \;\;\;\;\left| \; \cdot \; M \right.$ $n \cdot M = m$

Also berechnet man die Masse einer gegebenen Stoffmenge durch die Gleichung:

$m = n \cdot M$ oder $Masse = Stoffmenge \cdot Molmasse$ Einheiten $mol \cdot \frac{g}{mol} = g$

Wieviel 0,44 mol Aluminium sind, sollte mit dieser Formel kein Problem sein, oder?

AUFGABE 6 - Bestimme Massen

Wieviel wiegen die angegebenen Mengen der Stoffe?

WICHTIG: Denk daran, dass du bei allen Aufgaben die Molmasse der betrachteten Stoffes zuerst berechnen musst!

$0,44 \ mol \ Aluminium, \ 0,6 \ mol \ Wasserstoff$, $2,3 \ mol \ PbO_2$, $1/3 \ mol$ von $2 Al_2O_3$, $5 \ mol \ Wasser$

LÖSUNG - Aufgabe 6

• $0,44 \ mol \ Aluminium$: $M(Al)=27 \frac{g}{mol}$, $m = 11,88 g$
• $0,6 \ mol \ Wasserstoff$: $M(H_2)=2 \frac{g}{mol}$, $m = 1,2 g$
• $2,3 \ mol \ PbO_2$: $M(PbO_2)=239,2 \frac{g}{mol}$, $m = 550,16 g$
• $1/3 \ mol$ von $2 Al_2O_3$: $M(Al_2O_3)=102 \frac{g}{mol}$, $m = 34 g$
• $5 \ mol \ Wasser$ : $M(H_2O)=18 \frac{g}{mol}$, $m = 90 g$

Das Molvolumen

Schauen wir nun noch einmal zurück auf den Satz von Avogadro:

Satz von Avogadro

Alle Gase enthalten bei gleicher Temperatur und gleichem Druck in gleichen Volumina die gleiche Teilchenzahl.

Warum ist der Satz von Avogadro auch wichtig im Zusammenhang mit der Stoffmenge? Beide haben die Gemeinsamkeit, dass es um Teilchenanzahlen geht.

Vergleicht man zum Beispiel 1 l von zwei verschiedenen Gasen, so haben nach dem Satz von Avogadro beide Gase die gleiche Anzahl an Teilchen. Wenn die Anzahl der Teilchen gleich ist, dann ist auch die Stoffmenge von einem Liter eines Gases identisch.

Überträgt man das auf 1 mol von Gasen, wo man ja immer die gleiche Teilchenanzahl hat, dann müsste man also auch sagen können, das 1 mol eines beliebigen Gases immer das gleiche Volumen hat.

Molvolumen

1 mol eines beliebigen Gases hat bei gleichen Bedingungen (Druck und Temperatur) das gleiche Volumen, nämlich $V_m = 22,4 \frac{l}{mol}$.

Dies bezeichnet man als Molvolumen oder Molares Volumen.

Aber Achtung! Die Benutzung des Molvolumens macht nur bei der Betrachtung von Gasen Sinn, denn bei allen Gasen ist $V_m = 22,4 \frac{l}{mol}$. Bei Feststoffen und Flüssigkeiten könnte man das Molvolumen zwar auch bestimmen, aber die Volumina sind alle verschiedenen.

Überlegen wir kurz, was uns das Molvolumen bringt? Im Prinzip können wir nun das Volumen von Gasen in Stoffmengen und dann auch in Massen umrechnen.

Herleitung einer Formel zum Rechnen mit dem Molvolumen

Um eine Formel zu finden, mit der man aus einem gegebenen Volumen die Stoffmenge oder umgekehrt aus der Stoffmenge das Volumen berechnen kann, kann man sich den Dreisatz bzw. die proportionalen Zuordnungen zur Hilfe nehmen:

einem Volumen von $22,4 \ l$ entspricht die Stoffmenge $1 mol$

ein bleibiges Volumen $V$ entspricht der Stoffmenge $n$

Wegen der Quotientgleichheit muss gelten:

$\frac{22,4 \ l}{ 1 \ mol} = \frac{V}{n}$

daraus ergibt sich:

$22,4 \frac{l}{mol} = \frac{V}{n}$

oder:

$V_m = \frac{V}{n}$

Berechnung mit Stoffmengen und Volumen

Die Stoffmenge kann aus dem Gasvolumen mit der folgenden Formel berechnet werden:

$n=\frac{V}{V_m}$

Umgekehrt kann das Volumen eines Gases aus der Stoffmenge berechnet werden:

$V = n \cdot V_m$

Und nun ein paar Aufgaben, bei den es viele kleine Gemeinheiten gibt ;-) Es geht um verschiedene große und kleine Einheiten, wann man mit der Molvolumen rechnen kann und was tun wenn es nicht geht.

Mal schauen, wie viele Aufgaben du richtig haben wirst?

AUFGABE 7 - Rechnungen rund die Stoffmenge und um Volumina

Wenn möglich, sollten die Rechnungen immer unter Verwendung der Stoffmenge geschehen und nicht ohne sie!

a.) Berechne das Volumen:

0,31 mol Kohlendioxid ; 2,8 mol Aluminium ; 11 mol Chlor ; 25 g Ammoniak NH₃ (ohne die Dichte!)

b.) Berechne die Stoffmenge:

1500 l Schwefelwasserstoff, 42 l Luft , 15 ml Sauerstoff , 1 l Wasser, 3000 m³ Methan (passen in das alte Gasometer in Zwickau, Bild rechts)

LÖSUNG zu Aufgabe 7

Die Formel spielt hier absolut keine Rolle, auch nicht, dass zum Beispiel Chlor Cl₂ ist. Allerdings kann man bei Aluminium und Wasser nicht mit dem Molvolumen rechnen, da es beides keine Gase ist!

TIPP: Schreibe die Rechnung mit den Einheiten auch, damit du siehst, dass beim Ergebnis auch die richtige Einheit herauskommt.

a.)

• Kohlendioxid: n = 0,31 mol enstpricht V = 6,94 l
• Aluminium: n = 2,8 mol, mit M = 27 g/mol ergibt m = 75,6 g, mit der Dichte ρ = 2,7 g/cm³ kommt man auf V = 28 cm³
• Chlor: n = 11 mol entspricht V = 246,4 l
• Ammoniak: m = 25 g, mit M = 17 g/mol ergibt sich n = 1,47 mol, das entspricht V = 32,94 l

b.)

• Schwefelwasserstoff H₂S : V = 1550 l entsprechen n = 67 mol
• Luft (egal wie die Zusammensetzung ist!): V = 42 l entsprechen 1,875 mol
• Sauerstoff: V = 15 ml = 0,015 l entsprechen n = 6,696·10^-4 mol = 0,6696 mmol (Millimol)
• Wasser: Dichte sollte bekannt sein, daher 1 l = 1000 g Wasser, mit M = 18 g/mol ergibt sich n = 55,56 mol
• Methan: 3.000 m³ = 3.000.000 l, entsprechen n = 133.928,57 mol

AUFGABE 8 - Druckluftgasbehälter bom Sporttauchen

Tauchen nehmen ihre Luft zum Tauchen mit unter Wasser. Ein üblicher Behälter umfasst etwa 20 l. Wieviel mol Luft ist in der Flasche enthalten?

LÖSUNG zu Aufgabe 8

Das Molvolumen von 22,4 l/mol gilt nur für Normaldruck. Die die in den Gasflaschen enthaltene Luft aber unter erhöhtem Druck steht (Druckgasbehälter!) kann ich hier nichts berechnen, ohne zu wissen, unter welchem Druck das Gas im Behälter steht.

Wenn man den Druck kennen würde, könnte man die allgemein Gasgleichung nehmen, nach der gilt: ${p \cdot V \over T} = konst$.

So könnte man von erhöhtem Druck auf "Normaldruck" herunterrechnen.

Allerdings ... mit dem berechneten Volumen kann man dann auch nicht so einfach die Tauchzeit berechnen, denn unter Wasser, bei erhöhten Druck, nimmt der Luftverbrauch zu. So gibt es für das Tauchen meist spezielle Formeln, mit denen man mit dem Flaschen-Volumen, dem Druck in der Flasche und der Tauchtiefe die mögliche Tauchzeit berechnen kann.