Benutzer:KaJa123/ Nullstellen und Schnittpunkte linearer Funktionen
Benutzer:KaJa123/ Nullstellen und Schnittpunkte linearer Funktionen
Nullstellen und Schnittpunkte linearer Funktionen
Um dein Vorwissen zu aktivieren, starten wir mit einen Quiz zu linearen Funktionen!
Nullstellen einer Funktion
🎯 Lernziele
- Du verstehst, was Nullstellen sind und wie man sie interpretieren kann.
- Du kannst Nullstellen grafisch und algebraisch bestimmen.
- Du kannst digitale Werkzeuge wie GeoGebra einsetzen.
- Du kannst Nullstellen in realen Kontexten deuten.
1️⃣ Einstieg
Wann ist es wichtig zu wissen, wann eine Funktion den Wert 0 hat?
- Wurf: Wann trifft der Ball den Boden?
- Gewinn: Wann ist der Gewinn null?
- Gerade: Wo schneidet die Funktion die x-Achse?
Definition Nullstelle: "Die Nullstelle ist der x-Wert, bei dem y=0 ist." Also f(x)=0.
Grafisch bedeutet das: Der Graph schneidet die x-Achse.Falls du es noch nicht ganz verstanden hast, kannst du dir das Erklär-Video anschauen!
Mini-Check
Blau:
Rot:
Grün:
Schnittpunkte
Im folgenden Abschnitt wirst du dich näher mit Schnittpunkten zweier linearer Funktionen beschäftigen. Zu jeder Aufgabe werden Hilfestellungen gegeben, falls du mal selbst nicht auf einen Rechenweg kommen solltest. Notiere deine Rechnung, falls nicht anders angegeben, immer in deinem Heft.
Frau Müller möchte einen neuen Streaming-Vertrag abschließen. Sie vergleicht dazu unterschiedliche Anbieter und stoßt auf folgende Angebote:
- Streaming-Anbieter A: 10€ einmalige Startgebühr, 8€ monatliche Gebühr
- Streaming-Anbieter B: keine Startgebühr, 10€ monatliche Gebühr
- Erstelle eine Tabelle, die die Entwicklung der Gebühren darstellt.
- Stelle die Entwicklung der Gebühren mit Hilfe deiner Tabelle graphisch dar.
- Was ist an den Graphen abzulesen? Wie könntest du die Entwicklung formal ausdrücken?
- Die Graphen schneiden sich im Punkt (5|50). Im Sachkontext bedeutet es, dass Streaming-Anbieter A nach fünf Monaten langfristig günstiger ist.
Betrachtet man zwei lineare Funktionen f(x) und g(x), können diese drei Beziehungen beobachtet werden:
1. f(x) und g(x) sind identisch ⇒ für alle x ist f(x)=g(x)
2. f(x) und g(x) schneiden sich in einem Punkt ⇒ für ein x ist f(x)=g(x)
3. f(x) und g(x) sind parallel ⇒ für kein x ist f(x)=g(x)
→ In unserem Fall interessiert uns am meisten der 2. Fall. Wenn sich zwei Geraden schneiden, dann nennen wir den Schnittpunkt SP(x|y). An diesem Punkt sind die Werte von f(x) gleich zu denen von g(x) (→f(x)=g(x))
Falls du es noch nicht ganz verstanden hast, kannst du dir das Erklär-Video anschauen!
Sophie und Michel möchten im Frühjahr heiraten. Um ihren Gästen eine unkomplizierte Heimfahrt zu ermöglichen, möchten sie ein Taxi-Unternehmen buchen, welches einen Shuttle-Service anbietet. Das Taxi-Unternehmen bietet zwei Optionen an:
- Tarif A: 100€ Pauschaule + 1,50€ pro km
- Tarif B: keine Grundgebühr, aber 3,50€ pro km
- Erstelle eine Tabelle, die die Entwicklung der Gebühren darstellt.
- Stelle die Entwicklung der Gebühren mit Hilfe deiner Tabelle graphisch dar.
- Was ist an den Graphen abzulesen? Wie könntest du die Entwicklung formal ausdrücken?
- Die Graphen schneiden sich im Punkt (50|175). Im Sachkontext bedeutet es, dass der Tarif A ab 175 Gesamtkilometern besser ist. Bis 175 Gesamtkilometer lohnt sich Tarif B mehr.
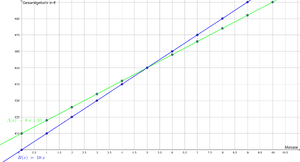
Zwei Fahrzeuge A und B fahren auf derselben Straße in dieselbe Richtung.
- Fahrzeug A startet um 8:00 Uhr an einem Rastplatz und fährt mit einer konstanten Geschwindigkeit von 60 km/h.
- Fahrzeug B startet ebenfalls um 8:00 Uhr, jedoch 20 km hinter dem Rastplatz, und fährt mit einer konstanten Geschwindigkeit von 80 km/h.
An welchen Ort überholt Fahrzeug B das andere Fahrzeug?
- Lege eine Variable t fest, die die Zeit in Stunden seit 8:00 Uhr beschreibt. Stelle für beide Fahrzeuge eine lineare Funktion auf, die die zurückgelegte Strecke s (in km) in Abhängigkeit von der Zeit t beschreibt.
- Stelle die beiden Funktionen in einem Koordinatensystem grafisch dar oder visualisiere die Entwicklung tabellarisch.
- Berechne den Schnittpunkt der beiden Funktionen und interpretiere ihn. (Nach welcher Zeit befinden sich beide Fahrzeuge am gleichen Ort?)
- Überprüfe, ob das Ergebnis im Sachzusammenhang sinnvoll ist, und begründe deine Antwort.
- Die Graphen schneiden sich im Punkt (60|60). Im Sachkontext bedeutet es, dass die Fahrzeuge nach 60 min (1h) sich in 60km Entfernung des Rastplatzes befinden. Fahrzeug B überholt Fahrzeug A also bei Jedha. Die zurückgelegten Strecken in Abhängigkeit von der Zeit in min kann durch A(t)=t und B(t)=8/6t-20 beschrieben werden.
Jetzt bist du gefragt! Überlege dir deine eigene Aufgabe mit Alltagsbezug! Formuliere dafür eine Situationsbeschreibung, die Aufgabenstellung und rechne deine Aufgabe zur Überprüfung durch. Lade dein Ergebnis in das Padlet hoch, sodass deine Mitschüler:innen sich an deinen Aufgaben probieren können! Falls es nicht funktioniert nutze den Link: https://padlet.com/karolinaiwonaszymiczek/eure-eigenen-aufgaben-m1piqjedetmvczin
Dir fehlen Ideen? Nutze eine KI-Plattform, um eine kreative Aufgabe zu erstellen. Kennzeichne deine Nutzung in Klammern hinter der Überschrift im Padlet. Löse die Aufgaben anschließend eigenständig!
Zwei lineare Funktionen haben die allgemeine Form f(x)= mx+b (). Dabei gibt der Wert m() die Steigung der Geraden an. Der Wert b () heißt y-Achsenabschnitt und gibt den Schnittpunkt der Funktion mit der y-Achse() an. Der Schnittpunkt zweier Geraden ist der Punkt, an dem beide Geraden den gleichen x-Wert () zum selben y-Wert () besitzen. Der Schnittpunkt kann durch das Gleichsetzen () von f(x) und g(x) berechnet werden, also schreibt man f(x)=g(x) (). Man löst die Gleichung dann nach x () auf. Dieser Wert ist die x-Koordinate des Schnittpunktes. Anschließend setzt man den Wert in eine der beiden Funktionen () ein, um die y-Koordinate zu berechnen. Haben zwei Geraden die gleiche () Steigung, aber unterschiedliche y-Achsenabschnitte, so sind sie parallel () und haben keinen Schnittpunkt. Sind sowohl Steigung als auch y-Achsenabschnitt gleich (), so sind die Geraden identisch () und haben unendlich viele Schnittpunkte. Wenn man eine Sachaufgabe hat, müssen wir zuerst die Situation mathematisieren () und die entsprechenden Funktionen aufstellen. Anschließend berechnen wir die Schnittpunkte. Zuletzt deuten () wir die Ergebnisse im Sachkontext.
