Atommodelle im Wandel der Zeit/Bohr
Das Schalenmodell nach Nils Bohr ist eine Weiterentwicklung des Kern-Hülle-Modells. Auf dieser Seite findest du viele Informationen dazu, welche konkreteren Informationen die Wissenschaftler nach Ernest Rutherford noch zum Atomkern und der Atomhülle entdeckt haben. Es bietet sich an, die Informationen auf dieser Seite arbeitsteilig durchzuarbeiten: Ein Teil der Lerngruppe beschäftigt sich mit dem Atomkern, ein anderer Teil der Lerngruppe beschäftigt sich mit der Atomhülle. Am Ende erklären sich immer zwei Schüler*innen gegenseitig, was sie herausgefunden haben und erstellen gemeinsam einen Post, in dem Nils Bohr sein Modell kurz und knapp vorstellt.
Der Atomkern
Im Zusammenhang mit seinem Streuversuch untersuchte Rutherford den Aufbau des Atomkerns genauer. Er fand dabei nicht nur heraus, dass die positive Ladung des Atomkerns mit steigender Ordnungszahl im Periodensystem immer stärker wird, sondern auch, dass diese Zunahme einer gewissen Gesetzmäßigkeit folgt: Wenn man der positiven Ladung des Wasserstoff-Atomkerns den Wert "+1" zuschreibt, hat der Atomkern des Heliums die Ladung "+2", der Kern des Lithiums die Ladung "+3" und so weiter. Die Ladung des Atomkerns eines Elements entspricht also genau der Ordnungszahl im Periodensystem.
Rutherford schloss daraus im Jahr 1919, dass es ein positiv geladenes Elementarteilchen geben muss, das genau die Ladung "+1" hat. Dieses Teilchen nannte er Proton. Die Ordnungszahl eines Elements gibt damit an, wie viele Protonen sich im Atomkern befinden.
Beispiel: Magnesium hat die Ordnungszahl 12. Im Atomkern des Magnesium-Atoms gibt es also 12 Protonen.
1932 konnte James Chadwick beweisen, dass es im Atomkern noch eine zweite Sorte von Elementarteilchen gibt. Da dieses neu entdeckte Teilchen keine elektrische Ladung hat, nannte er es Neutron. Die Rolle der Neutronen liegt in erster Linie darin, die positiv geladenen Protonen zusammenzuhalten und eine Abstoßung zu verhindern.
Sowohl die Protonen als auch die Neutronen haben jeweils die Masse 1 u. Die Masse der Elektronen in der Atomhülle hingegen ist so gering, dass sie sich nicht auf die Massenzahl eines Atoms auswirkt. Mithilfe der Ordnungszahl und der Massenzahl eines Elementes kann man also berechnen, wie viele Neutronen sich im Atomkern befinden.
Beispiel: Im Periodensystem wird das Element Kalium so dargestellt:
Kalium hat also die Ordnungszahl 19. Das bedeutet, im Atomkern gibt es 19 Protonen. Diese Protonen habe zusammen eine Masse von . Da Kalium die Massenzahl 39 hat, muss es im Atomkern noch Neutronen geben.
Verständnisaufgaben zur Aufbau des Atomkerns
Erkläre stichpunktartig den Zusammenhang zwischen Ordnungs- und Protonenzahl sowie zwischen Massenzahl und Neutronenzahl am Beispiel des Atomkerns von .
Gib die Anzahl der Protonen und Neutronen für folgende Atome an: , ,
...
Die Atomhülle
Energiestufenmodell
Niels Bohr veröffentlichte im Jahr 1913 ein Atommodell, das Vorstellungen zur Atomhülle lieferte, die deutlich detaillierter waren als die Ideen aus Rutherfords Kern-Hülle-Modell. Bohr setzte sich damit auseinander, wie viel Energie benötigt wird, um einzelne Elektronen aus der Hülle eines Atoms zu entfernen. Dabei entstehen geladene Teilchen, die sogenannten Ionen. Die Energie, die zur Entfernung eines Elektrons aus der Atomhülle benötigt wird, heißt dementsprechend Ionisierungsenergie.
Als Beispiel betrachten wir zunächst ein Aluminium-Atom. Aluminium ist das Element mit der Ordnungszahl 13. Dementsprechend befinden sich im Kern eines Aluminium-Atoms 13 Protonen und in seiner Hülle 13 Elektronen.
Erkunde mithilfe des folgenden Applets, wie viel Energie jeweils zum Entfernen der einzelnen Elektronen eines Aluminium-Atoms benötigt wird. Bewege dazu den Schieberegler, beschreibe die Entwicklung der Ionisierungsenergien und notiere besondere Auffälligkeiten.
Notfall-Link bei Problemen mit dem Applet
Bei den Experimenten zu Messung der Ionisierungsenergien befinden sich Schritt für Schritt immer weniger Elektronen in der Atomhülle, während die Anzahl der Protonen im Atomkern konstant bleibt. Die Anziehungskraft der gleichbleibenden positiven Ladung des Kerns verteilt sich dabei auf immer weniger Elektronen, sodass die verbleibenden Elektronen immer stärker "festgehalten" werden. Aus diesem Grund wird immer mehr Energie zum Entfernen der Elektronen benötigt. Diese Überlegungen lassen sich schon durch das Kern-Hülle-Modell begründen.
Aber wie kommt zu den sprunghaften Anstiegen der Ionisierungsenergie zwischen dem 3. und 4. bzw. zwischen dem 11. und 12. Elektron des Aluminium-Atoms? Bei der Erklärung dieser Beobachtungen kommt das Kern-Hülle-Modell an seine Grenzen. Nach dem Bohr'schen Atommodell markieren diese Energie-Sprünge die Grenzen zwischen verschiedenen Energiestufen. Je höher die Energiestufe ist, auf der sich ein Elektron befindet, desto leichter lässt es sich entfernen. Die Verteilung der Elektronen auf die Energiestufen wird als Elektronenkonfiguration bezeichnet.
Beim Aluminium-Atom sind drei Energiestufen besetzt. Die Elektronen aus der 3. Energiestufe werden zuerst entfernt, die Elektronen der 1. Energiestufe zuletzt.
Im folgenden Applet wurde die Darstellung aus Aufgabe 1 ergänzt. Du siehst nun links neben dem Koordinatensystem die Elektronenkonfiguration des Aluminiums nach Bohrs Energiestufenmodell. Verdeutliche dir die Informationen aus dem Info-Text, indem du noch einmal das Entfernen der Elektronen mithilfe des Schiebereglers simulierst.
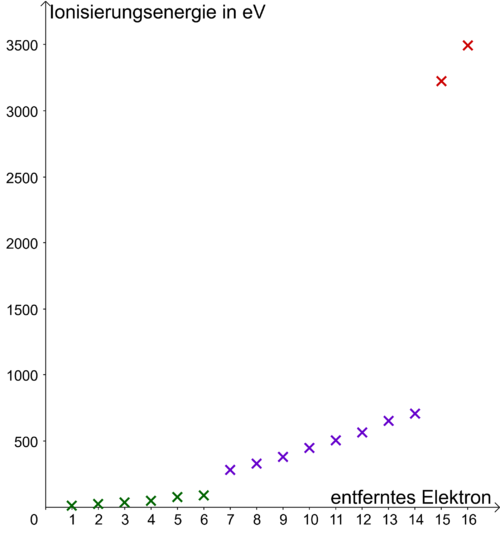
Die Abbildung zeigt die Ionisierungsenergien für die Elektronen im Schwefel-Atom. Zeichne analog zu Aufgabe 2 die Verteilung der Elektronen auf die Energiestufen im Schwefel-Atom.
Fülle die Lücken so, dass die Angaben der Reihenfolge entsprechen, in der die Energiestufen vom oben nach unten im Modell auftauchen!
Auf der 3.|dritten() Energiestufe befinden sich 6|sechs() Elektronen.
Auf der 2.|zweiten() Energiestufe befinden sich 8|acht() Elektronen.
Auf der 1.|ersten() Energiestufe befinden sich 2|zwei() Elektronen.
Der Abstand zwischen der ersten und zweiten Energiestufe ist deutlich größer() als der Abstand zwischen der zweiten und dritten Energiestufe.
Schalenmodell
Auf der Basis des Energiestufenmodells wurde auch die anschauliche Vorstellung vom Aufbau eines Atoms überarbeitet. Im Schalenmodell werden die unterschiedlichen Energiestufen als unterschiedliche Abstände der Elektronen zum Atomkern interpretiert. Die Elektronen befinden sich in unterschiedlichen Schalen, die den Atomkern kugelförmig umgeben.
Auch im folgenden Applet geht es wieder um die Elektronenkonfiguration des Aluminiums. Die Darstellung im Energiestufenmodell wird der Darstellung im Schalenmodell gegenübergestellt. Erkunde den Zusammenhang zwischen den beiden Modellen mithilfe des Schiebereglers und erläutere deine Beobachtungen.
Die Elektronenschalen werden nach außen hin immer großer. Deshalb passen in die äußeren Schalen mehr Elektronen hinein, als in die erste, innerste Schale. Bei den Hauptgruppenelementen der ersten Perioden beinhaltet die innere Schale bis zu 2 Elektronen und alle weiteren bis zu 8 Elektronen. Die Elektronenschalen werden dabei von innen nach außen nach und nach besetzt. Das bedeutet, dass eine zusätzliche Schale erst dann begonnen wird, wenn die vorhandenen voll besetzt sind.
Zusammenfassende Aufgaben
Teste dein Wissen zum Bohr'schen Atommodell mit dem folgenden Quiz:
Die folgende Übung hat es in sich! Jedes Feld steht für ein anderes Hauptgruppenelement. Nimm ein Periodensystem zur Hilfe und ordne die Kärtchen dem richtigen Feld zu.
Notfall-Link bei Problemen mit dem Applet
Stell dir vor, auch Niels Bohr wäre wie seine Vorgänger auf Instagram aktiv gewesen. Erstelle auch zum Schalenmodell einen Post, in dem die wesentlichen Aspekte zum Aufbau des Atomkerns angerissen werden.
Hier findest du einen Generator für Instagram-Posts.
Die Idee des historisch-genetischen Ansatz es zur Entwicklung des Atommodells findet sich auch in einem MINT-EC Themenheft. Florian Spieler setzt es dort in Form von Briefen um, die die Wissenschaftler austauschen. Die Umsetzung durch kurz gehaltene Social-Media-Beiträge soll die Erarbeitung näher an die Lebenswelt der Schülerinnen und Schüler heranrücken und dadurch kurzweiliger gestalten. [1]
- ↑ Spieler, Florian (2018): Von Demokrit zu Bohr – die historische Genese des Atommodells in: Verein MINT-EC: Alles Chemie - Atombau und PSE. Abrufbar unter https://www.lncu.de/files/coursemanager/contentfile/780/Chemie_A_22_ONLINE_c.pdf [26.10.2019]
