Alles rund um Quadratische Funktionen

Info

In diesem Lernpfad geht es darum, dein Wissen im Bereich quadratischer Funktionen zu vertiefen.

Dazu werden dir Informationen und Aufgaben zur Scheitelpunktform, der Umwandlung zwischen Scheitelpunktform und Normalform sowie zur Berechnung von Nullstellen bereitgestellt. Zusätzlich erwarten dich zwei Anwendungsaufgaben, in welchen du die zuvor gelernten Inhalte testen kannst.

In diesem Lernpfad findest du Aufgaben mit einem *. Bei diesen handelt es sich um Forderaufgaben. Aufgaben mit ** sind anspruchsvolle Knobelaufgaben. Hat eine Aufgabe kein *, dann ist die Aufgabe zur Wiederholung und Vertiefung der Inhalte geeignet.

Scheitelpunktform

1. Die Scheitelpunktform

Fülle den folgenden Lückentext aus, indem du die passenden Silben einfügst.

Wir schauen uns die Funktion $g(x)=a\cdot (x-d)^{2}+e$ an. Funktionen dieser Art heißen quadratische Funktionen. Der Graph einer solchen Funktion ist eine Parabel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Scheitelpunkt. Liegt die Funktionsgleichung in der Scheitelpunktform vor, wie es hier der Fall ist, dann kann der Scheitelpunkt $S$ direkt aus der Funktionsgleichung abgelesen werden. Der Parameter $d$ ist die $x$ -Koordinate und der Parameter $e$ ist die $y$ -Koordinate des Scheitelpunkts. $\Rightarrow S(d|e)$ .
Ist der Parameter $a$ kleiner als Null ( $a<0$ ), dann ist der Graph der Funktion $g$ nach unten geöffnet.
Ist $a$ größer als Null ( $a>0$ ), dann ist der Graph von $g$ nach oben geöffnet.
Ist $a$ größer als Eins ( $a>1$ ) oder kleiner als minus Eins ( $a<-1$ ), dann sieht der Graph von $g$ schmaler aus. Man sagt, dass in diesem Fall der Graph gestreckt wird.
Liegt $a$ zwischen minus Eins und Eins ( $-1<a<1$ ), dann sieht der Graph von $g$ breiter aus. Man sagt, dass in diesem Fall der Graph gestaucht wird.

Ist $d$ größer als Null ( $d>0$ ), dann wird der Graph von $g$ nach rechts verschoben.
Ist $d$ kleiner als Null ( $d<0$ ), dann wird der Graph von $g$ nach links verschoben.

Ist $e$ kleiner als Null ( $e<0$ ), dann wird der Graph von $g$ nach unten verschoben.
Ist $e$ größer als Null ( $e>0$ ), dann wird der Graph von $g$ nach oben verschoben.

Entdecke

Hier kannst du den Einfluss der einzelnen Parameter der Scheitelpunktform $a,d,e$ auf den Funktionsgraphen erkunden. Bewege dafür jeweils die Schieberegler und beobachte wie sich der Graph von $f$ verändert.

2.WANTED! Welche Punkte gehören nicht zu der Funktion f?

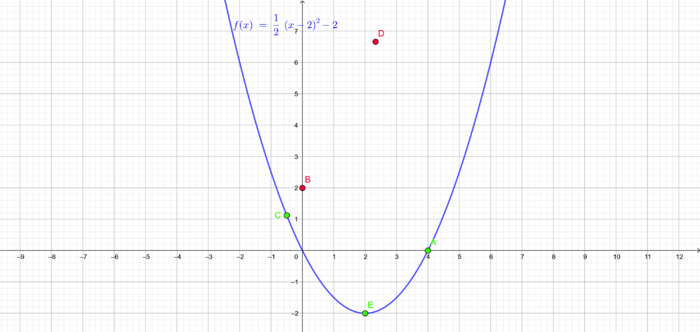
Gegeben seien die Funktion $f(x)={\frac {1}{2}}\cdot (x-2)^{2}-2$ und die Punkte

$A=(4|0),$

$B=(0|2),$

$C=(-{\frac {1}{2}}|{\frac {9}{8}}),$

$D=({\frac {7}{3}}|{\frac {20}{3}})$ und

$E=(2|-2)$ .

a) Überprüfe rechnerisch, ob die Punkte $A,B,C,D$ und $E$ auf dem Graphen von $f$ liegen.

Du kannst einfach prüfen, ob ein Punkt auf dem Graphen liegt: Setze den

x

-Wert in die Funktionsgleichung ein und berechne den zugehörigen

y

-Wert

Die Punkte $A,C$ und $E$ liegen auf dem Graphen, die Punkte $B$ und $D$ nicht.

${\begin{array}{rlll}A&&=&&(4|0):\\f(4)&&=&&{\frac {1}{2}}\cdot (4-2)^{2}-2={\frac {1}{2}}\cdot 2^{2}-2={\frac {1}{2}}\cdot 4-2=2-2=0\\\\B&&=&&(0|2):\\f(0)&&=&&{\frac {1}{2}}\cdot (0-2)^{2}-2={\frac {1}{2}}\cdot (-2)^{2}-2={\frac {1}{2}}\cdot 4-2=2-2=0\neq 2\\\\C&&=&&(-{\frac {1}{2}}|{\frac {9}{8}}):\\f(-{\frac {1}{2}})&&=&&{\frac {1}{2}}\cdot (-{\frac {1}{2}}-2)^{2}-2={\frac {1}{2}}\cdot (-{\frac {5}{2}})^{2}-2={\frac {1}{2}}\cdot {\frac {25}{4}}-2={\frac {25}{8}}-2={\frac {9}{8}}\\\\D&&=&&({\frac {7}{3}}|{\frac {20}{3}}):\\f({\frac {7}{3}})&&=&&{\frac {1}{2}}\cdot ({\frac {7}{3}}-2)^{2}-2={\frac {1}{2}}\cdot ({\frac {1}{3}})^{2}-2={\frac {1}{2}}\cdot {\frac {1}{9}}-2=-{\frac {1}{18}}-2=-{\frac {35}{18}}\neq {\frac {20}{3}}\\\\E&&=&&(2|-2):\\f(2)&&=&&{\frac {1}{2}}\cdot (2-2)^{2}-2={\frac {1}{2}}\cdot 0^{2}-2={\frac {1}{2}}\cdot 0-2=0-2=-2\\\end{array}}$

b) Zeichne den Graphen der Funktion $f$ und die Punkte $A-E$ in dein Heft. Vergleiche anschließend die Ergebnisse aus a) mit deiner Zeichnung

Du hast Probleme beim Zeichnen des Graphen? Der Lückentext in Aufgabe 1 hilft dir weiter.

Starte beim Zeichnen mit dem Scheitelpunkt, den du aus der Funktionsgleichung ablesen kannst. Auch hierbei kann dir Aufgabe 1 helfen.

Beim Zeichnen des Funktionsgraphen gibt dir der Parameter

a

an, wie viele Einheiten du nach oben oder unten "gehen" musst, wenn du eine Einheit nach rechts oder links "gehst".

Wenn deine Zeichnung so aussieht, hast du alles richtig gemacht:

3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?

Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. Hinweis: Du kannst die Bilder der Funktionsgraphen vergrößern, indem du mit der Maus auf diese klickst.

Betrachtet man die Funktionsgleichung

j(x)=a\cdot (x-d)^{2}+e

, so steht

d

für die Verschiebung in

x

-Richtung. Ist das Vorzeichen vor dem

d

dabei negativ, so verschiebt man den Graphen nach rechts und wenn es positiv ist nach links. Das

e

steht für die Verschiebung in

y

-Richtung nach oben, falls

e

positiv ist und nach unten wenn es negativ ist.

Betrachtet man die Funktionsgleichung $j(x)=a\cdot (x-d)^{2}+e$ , so beschreibt $a$ die Streckung (falls $a>1$ ) oder die Stauchung (falls $a<1$ ). Man geht vom Scheitelpunkt aus um eine Einheit nach links oder rechts und dann um $a$ Einheiten nach oben (falls $a$ negativ ist nach unten).

Falls

a<1

ist, oder generell ein Bruch ist, kann dies manchmal schwierig sein, da sich zum Beispiel

{\frac {2}{3}}

nicht so einfach ablesen lässt. Hierfür kann man die Normalparabel

x^{2}

betrachten. Sinnvoll ist es nun den Nenner, also

3

einzusetzen. Somit erhält man

3^{2}=9

. Die erhaltene Zahl muss man nun mit dem Bruch multiplizieren

9*{\frac {2}{3}}=6

. Man geht nun vom Scheitelpunkt um die eingesetzte Zahl nach links oder rechts (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} ) und um die am Ende erhaltene Zahl nach oben (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 6} ), oder nach unten falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ ist. (Wenn du hier noch Probleme hast scrolle hoch zum GeoGebra-Applet und verschiebe den Regler für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} . Beobachte dabei wie sich der Graph verändert.)

Beispiele sind:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=(x-3)^2+2} hat ihren Scheitelpunkt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (3| 2)}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=(x+0)^2-4} hat ihren Scheitelpunkt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (0| -4)}

4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktform aufstellen

Stell die zugehörigen Funktionsgleichungen in Scheitelpunktform auf. Wähle im Anschluss die richtige Lösung aus (Du musst in der App runterscrollen).

Überlege dir zunächst, welche Parameter du brauchst um eine Funktionsgleichung in Scheitelpunktform aufzustellen. Falls du Aufgabe 1 schon bearbeitet hast, findest du dort nützliche Hinweise. Du kannst dir auch nochmal das GeoGebra-Applet (oben) anschauen und die Schieberegler bewegen um zu sehen wie sich der Graph und die Funktionsgleichung verändert.

Die Scheitelpunktform hat die Funktionsgleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e} . Für den Scheitelpunkt gilt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=(d|e)} . Wenn du also den Scheitelpunkt aus der Darstellung des Funktionsgraphen abliest und seine Koordinaten in die Funktionsgleichung einsetzt, musst du nur noch den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} bestimmen. Achte beim Einsetzen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} in die Funktionsgleichung darauf, dass sich das Vorzeichen durch das Minus in der Klammer der Funktionsgleichung einmal umkehrt.

Um den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} zu bestimmen gibt es verschiedene Möglichkeiten.

Möglichkeit 1: Du kannst einen beliebigen weiteren Punkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (x|y)} aus dem Graphen ablesen und in die Funktionsgleichung einsetzen. Im Anschluss musst du nur noch die Gleichung nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} auflösen. Bei Bedarf kannst Du gerne dein Heft benutzen, um dir Rechenschritte zu notieren.

Möglichkeit 2: Alternativ kannst du den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} auch direkt aus dem Graphen ablesen: Gehst du vom Scheitelpunkt aus um eine Einheit nach rechts, so entspricht Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} der Anzahl an Einheiten, die du nach oben (positives Vorzeichen) oder nach unten (negatives Vorzeichen) gehen musst, bis du wieder auf dem Graphen bist.

Falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<1} ist kann dies manchmal schwierig sein, da sich zum Beispiel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{2}{3}} nicht so einfach ablesen lässt. Hierfür kann man die Normalparabel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^2} betrachten. Sinnvoll ist es nun den Nenner, also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} einzusetzen. Somit erhält man Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3^2=9} . Die erhaltene Zahl muss man nun mit dem Bruch multiplizieren Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 9\cdot\frac{2}{3}=6} . Man geht nun vom Scheitelpunkt um die eingesetzte Zahl nach links oder rechts (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} ) und um die am Ende erhaltene Zahl nach oben (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 6} ), oder nach unten falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ ist. (Wenn du hier noch Probleme hast scrolle hoch zum GeoGebra-Applet und verschiebe den Regler für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} . Beobachte dabei wie sich der Graph verändert.)

5. Funktionsgleichung gesucht!

Im folgenden sind je der Scheitelpunkt und ein weiterer Punkt einer Funktion gegeben. Stelle mit diesen Informationen die zugehörige Funktionsgleichung in Scheitelpunktform auf (im Heft).

a) Wie lautet die Funktionsgleichung zu den Punkten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(2|1)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(3|5)} ?

b) Wie lautet die Funktionsgleichung zu den Punkten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(-\frac{1}{3}|-2)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(-3|0)} ?

c) Wie lautet die Funktionsgleichung zu den Punkten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(3|2)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(0|-\frac{5}{6})} ?

Die Scheitelpunktform hat die Funktionsgleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e} . Überlege dir, was die einzelnen Parameter beschreiben (schaue evtl. Aufgabe 1 nochmal an).

Für den Scheitelpunkt gilt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=(d|e)} . Wenn du also den Scheitelpunkt in die Funktionsgleichung einsetzt, musst du nur noch den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} bestimmen. Achte beim Einsetzen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} in die Funktionsgleichung darauf, dass sich das Vorzeichen durch das Minus in der Klammer der Funktionsgleichung einmal umkehrt.

Um den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} zu bestimmen musst du den Punkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P} in die Funktionsgleichung einsetzen und nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} auflösen.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e}

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(2|1)} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} ein: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-2)^2+1}

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(3|5)} ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && 5 &&=&& a\cdot(3-2)^2+1\\ &\Leftrightarrow& 5 &&=&& a\cdot 1^2+1\\ &\Leftrightarrow& 5 &&=&& a\cdot 1+1\\ &\Leftrightarrow& 4 &&=&& a\\ \end{array} }

Somit ergibt sich: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=4\cdot(x-2)^2+1}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e}

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(-\frac{1}{3}|-2)} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} ein: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x+\frac{1}{3})^2-2}

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(-3|0)} ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && 0 &&=&& a\cdot(-3+\frac{1}{3})^2-2\\ &\Leftrightarrow & 0 &&=&& a\cdot (-\frac{8}{3})^2-2\\ &\Leftrightarrow & 0 &&=&& a\cdot \frac{64}{9}-2\\ &\Leftrightarrow & 2 &&=&& \frac{64}{9}\cdot a\\ &\Leftrightarrow & \frac{9}{32} &&=&& a \end{array} }

Somit ergibt sich: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=\frac{9}{32}\cdot(x+\frac{1}{3})^2-2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e}

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(3|2)} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} ein: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-3)^2+2}

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(0|-\frac{5}{6})} ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && -\frac{5}{6} &&=&& a\cdot(0-3)^2+2\\ &\Leftrightarrow & -\frac{5}{6} &&=&& a\cdot (-3)^2+2\\ &\Leftrightarrow & -\frac{5}{6} &&=&& a\cdot 9+2\\ &\Leftrightarrow & -\frac{17}{6} &&=&& 9\cdot a\\ &\Leftrightarrow & -\frac{17}{54} &&=&& a\\ \end{array} }

Somit ergibt sich: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=-\frac{17}{54}\cdot(x-3)^2+2}

6. Anwendungsaufgabe für Zwischendurch: Flugbahn eines Steins

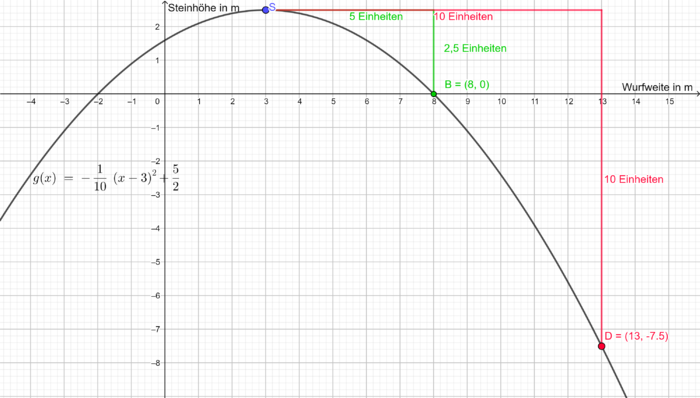
Jonas wirft einen Stein vom Ufer in einen See. Die Flugbahn des Steins lässt sich mit der quadratischen Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=-\frac{1}{10}\cdot(x-3)^2+\frac{5}{2}} beschreiben, wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} die Entfernung des Steins vom Ufer und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)} die Höhe des Steins (jeweils in Meter) beschreibt.

a) Nach wie vielen Metern erreicht der Stein seinen höchsten Punkt?

Da die Funktion eine negative Steigung besitzt, erreicht der Stein seinen höchsten Punkt am Scheitelpunkt der Funktion. Da die Funktion in Scheitelpunktform angegeben ist, kannst du diesen direkt aus der Funktionsgleichung ablesen.

Der Scheitelpunkt der Funktion ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=(3|\frac{5}{2})} . Der Stein erreicht seinen höchsten Punkt also nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} Metern.

b) Zeichne die Flugbahn des Steins in dein Heft.

Zu Erinnerung: Eine quadratische Funktion in Scheitelpunktform hat die Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e} . Um die Flugbahn zeichnen zu können, musst du die Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a,d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} der gegebenen Funktionsgleichung identifizieren.

Zeichne zunächst den Scheitelpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=(d|e)} ein. Beim weiteren Zeichnen des Funktionsgraphen hilft dir der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} . Da Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=-\frac{1}{10}<1} ist, ist dies etwas schwieriger. Hierfür kann man die Normalparabel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^2} betrachten.

Der Scheitelpunkt liegt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=(3|\frac{5}{2})} . Für $a=-{\frac {1}{10}}$ ist es sinnvoll den Nenner, also $10$ in $x^{2}$ einzusetzen. Somit erhält man $10^{2}=100$ . Die erhaltene Zahl muss man nun mit dem Bruch multiplizieren $100\cdot (-{\frac {1}{10}})=-10$ . Man geht nun vom Scheitelpunkt um die eingesetzte Zahl nach links oder rechts ( $10$ ) und um die am Ende erhaltene Zahl nach unten ( $10$ ), da die Zahl negativ war. Da somit die Zeichnung recht groß wird, kann man sich auch überlegen eine niedrigere Zahl in $x^{2}$ einzusetzen. Dies sollte am besten ein Teiler vom Nenner sein, z.B. $5$ . Das Vorgehen ist identisch: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 5^2=25 \Rightarrow 25\cdot (-\frac{1}{10})=-2,5} .

Beachte, dass die Flugbahn erst mit dem Abwurf des Steins beginnt und mit dem Auftreffen des Steins auf die Wasseroberfläche endet. Auf der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse trägst du die Wurfweite in Meter ab, auf der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achse die Höhe des Steins in Meter.

c)* In welcher Entfernung von Jonas taucht der Stein ins Wasser ein?

Um diesen Aufgabenteil zu lösen, musst du die Nullstellen der Funktion bestimmen (an einer dieser Nullstellen trifft der Stein auf das Wasser). Falls du dich dabei noch unsicher fühlst, bearbeite zuerst Aufgabe 9. Dort findest Du alle notwendigen Hilfestellungen. In jedem Fall solltest du für die Rechenschritte dein Heft benutzen.

Du musst zunächst die Nullstellen der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)} bestimmen. An einer dieser Nullstellen trifft der Stein auf die Wasseroberfläche.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && g(x) &&=&& 0 \\ &\Leftrightarrow& 0 &&=&& -\frac{1}{10}\cdot(x-3)^2+\frac{5}{2} &\mid \cdot(-10)\\ &\Leftrightarrow& 0 &&=&& (x-3)^2-25 &\mid +25 \\ &\Leftrightarrow& 25 &&=&& (x-3)^2 &\mid \sqrt{} \\ \end{array} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &\Rightarrow&(x_1-3) = -5& \textrm{sowie}& (x_2-3)=5\\ \end{array} }

Also folgt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1=-2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2=8} . Damit haben wir zwei Nullstellen.

Da wir jedoch davon ausgehen, dass Jonas den Stein nach vorne in den See wirft, beträgt die Wurfweite Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 8 m} .

Zusammenfassung zur Scheitelpunktform

Die allgemeine Scheitelpunktform lautet Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot (x-d)^2+e} .
Der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} ist der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert des Scheitelpunktes, wobei man hier immer das Vorzeichen in der Klammer umkehren muss.
Der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} ist der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert des Scheitelpunktes.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(d|e)} ist der Scheitelpunkt der Funktion.
Der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} wird als Streckungsfaktor bezeichnet.
- Ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a>1} wird die Funktion gestreckt, ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<1} wird die Funktion gestaucht.
- Ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} positiv so ist die Parabel nach oben geöffnet, ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ so ist sie nach unten geöffnet.
- Wenn man den Streckungsfaktor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} zum zeichnen nutzen möchte, geht man vom Scheitelpunkt aus um eine Einheit nach links oder rechts und dann um Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} Einheiten nach oben (falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ ist nach unten). Falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<1} ist, oder generell ein Bruch ist, kann dies manchmal schwierig sein. Hierfür kann man die Normalparabel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^2} betrachten. Sinnvoll ist es nun den Nenner einzusetzen. Die erhaltene Zahl muss man nun mit dem Bruch multiplizieren. Man geht nun vom Scheitelpunkt um die eingesetzte Zahl nach links oder rechts und um die am Ende erhaltene Zahl nach oben, oder nach unten falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ ist.
Hat man nur den Scheitelpunkt und einen weiteren Punkt gegeben und soll die zugehörige Funktionsgleichung aufstellen, so nimmt man sich die allgemeine Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot (x-d)^2+e} . Hier kann man den Scheitelpunkt einfach einsetzen für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} . Als nächstes setzt man den anderen Punkt für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} ein und formt nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} um.

Umwandlung Scheitelpunktform und Normalform

Bisher hast du dich intensiv mit der Scheitelpunktform beschäftigt. In diesem Abschnitt wirst du auch mit der Normalform einer quadratischen Funktion arbeiten. Diese lautet Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot x^2+b\cdot x+c}

Um die Scheitelpunktform in die Normalform zu überführen benötigst du die ersten beiden Binomischen Formeln.
Um die Normalform in die Scheitelpunktform zu überführen benötigst du die Methode der quadratischen Ergänzung.

Die ersten beiden Binomischen Formeln

1. Binomische Formel: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a+b)^2 = a^2+2ab+b^2}
2. Binomische Formel: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a-b)^2=a^2-2ab+b^2 }

Somit gilt:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} f(x) &&=&& a\cdot (x-d)^2+e\\ &&=&& a\cdot (x^2-2\cdot d\cdot x + d^2)+e\\ &&=&& a\cdot x^2-a\cdot 2\cdot d\cdot x + a\cdot d^2+e\\ &&=&& a\cdot x^2+b\cdot x+c \end{array} }

(mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b=-a\cdot 2\cdot d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c=a\cdot d^2+e} ).

Als Beispiel:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} f(x) &&=&& 2\cdot (x-4)^2+1\\ &&=&& 2\cdot (x^2-2\cdot 4\cdot x + 4^2)+1\\ &&=&& 2\cdot x^2-2\cdot 8\cdot x + 2\cdot 16+1\\ &&=&& 2\cdot x^2-16\cdot x+17 \end{array} }

quadratische Ergänzung

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} f(x) &&=&& a\cdot x^2+b\cdot x+c &\mid \text{Klammere a aus}\\ &&=&& a\cdot (x^2+\frac{b}{a}\cdot x+\frac{c}{a}) &\mid \text{Rechne} \frac{b}{a} \div 2 = d\\ &&=&& a\cdot (x^2+2\cdot d \cdot x+\frac{c}{a}) &\mid \text{addiere und subtrahiere d²}\\ &&=&& a\cdot ((x^2+2\cdot d \cdot x+d^2)-d^2+\frac{c}{a}) &\mid \text{fasse die innere Klammer zur binomischen Formel zusammen}\\ &&=&& a\cdot ((x+d)^2-d^2+\frac{c}{a}) &\mid \text{multipliziere a mit der Klammer}\\ &&=&& a\cdot (x+d)^2+a\cdot (-d^2+\frac{c}{a}) &\mid a\cdot (-d^2+\frac{c}{a})=e\\ &&=&& a\cdot (x+d)^2+e \end{array} }

Als Beispiel

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} f(x) &&=&& 2\cdot x^2+8\cdot x+9 &\mid \text{Klammere 2 aus}\\ &&=&& 2\cdot (x^2+\frac{8}{2}\cdot x+\frac{9}{2}) &\mid \text{Rechne} \frac{8}{2} \div 2 = 2=d\\ &&=&& 2\cdot (x^2+2\cdot 2 \cdot x+3) &\mid \text{addiere und subtrahiere d²=2²=4}\\ &&=&& 2\cdot ((x^2+2\cdot 2 \cdot x+4)-4+3) &\mid \text{fasse die innere Klammer zur binomischen Formel zusammen}\\ &&=&& 2\cdot ((x+2)^2-1) &\mid \text{multipliziere 2 mit der Klammer}\\ &&=&& 2\cdot (x+2)^2+2\cdot (-1)\\ &&=&& 2\cdot (x+2)^2-1 \end{array} }

7. Die Umwandlungen zwischen Scheitelpunktform und Normalform

Fülle den Lückentext aus, indem du auf eine Lücke klickst und die richtige Antwort auswählst.

8. Finde die Paare*

Wandle die Funktionen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g, f, o, m, p} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} in deinem Heft in die Normalform um und die Funktionen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j, l, k, i} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} in die Scheitelpunktform. Verbinde anschließend die Paare. Hinweis: Drei Funktionen haben keinen Partner.

9. Würdest du bei der Umwandlung zwischen der Scheitelpunktform und der Normalform auch Millionär werden?**

Wähle die Antwortmöglichkeit A,B,C oder D, welche die angefangene Gleichung zu einer korrekten quadratischen Gleichung ergänzt.

Die zum Lösen benötigten Formeln sind die binomischen Formeln.

Die binomischen Formeln lauten:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a+b)^2=a^2+2 \cdot ab+b^2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a-b)^2=a^2-2 \cdot ab+b^2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a+b)\cdot(a-b)=a^2-b^2}

Die Normalform

10. Die Normalform

Fülle den folgenden Lückentext aus, indem du die passenden Silben einfügst.

Wir schauen uns die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot x^2+b\cdot x+c} an. Diese Funktionsgleichung liegt in der Normalform vor. In dieser Form kann der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achsenabschnitt direkt abgelesen werden, es ist nämlich der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} . Ist der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} kleiner als Null (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<0} ), dann ist der Graph der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} nach unten geöffnet.
Der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} wird als Streckungsfaktor bezeichnet, wie auch in der Scheitelpunktform. Ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} größer als Null (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a>0} ), dann ist der Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} nach oben geöffnet.
Ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} größer als Eins (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a>1} ) oder kleiner als minus Eins (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<-1} ), dann sieht der Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} schmaler aus. Man sagt, dass in diesem Fall der Graph gestreckt wird.
Liegt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} zwischen minus Eins und Eins (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -1<a<1} ), dann sieht der Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} breiter aus. Man sagt, dass in diesem Fall der Graph gestaucht wird.

Entdecke

Hier kannst du den Einfluss der einzelnen Parameter der Normalform Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a, b, c } auf den Funktionsgraphen erkunden. Bewege dafür jeweils die Schieberegler und beobachte wie sich der Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f } verändert.

11. Funktionsgleichung gesucht!

Im folgenden sind je drei Punkte einer Funktion gegeben. Stelle mit diesen Informationen die zugehörige Funktionsgleichung in Normalform auf (im Heft).

a) Wie lautet die Funktionsgleichung zu den Punkten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(3|2), Q(-1|0)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R(0|7)} ?

Die Normalform hat die Funktionsgleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot x^2+ b\cdot x+c} . Überlege dir wie du die Punkte in diese Funktion einfügen kannst.

Setze die Punkte jeweils einzeln in die Funktionsgleichung ein (den ersten Wert für das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} und den zweiten Wert für das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} ). Du hast nun zwei verschiedene Gleichungen und bereits einen Wert für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} den du in die anderen Gleichungen einsetzten kannst.

Du hast verschiedene Verfahren gelernt um auf die anderen beiden Variablen zu kommen, das Einsetzungsverfahren und das Gleichsetzungsverfahren, wende eines der beiden an (natürlich ginge hier auch das Additionsverfahren, dieses ist allerdings etwas komplizierter).

Für das Einsetzungsverfahren musst du eine der Gleichungen nach einer Variable umstellen und dies dann für die Variable in die andere Gleichung einsetzen.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot x^2+b\cdot x+c}

Setze die Punkte Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P, Q} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R} in die allgemeine Gleichung ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} P(3|2): 2 &&=&& a\cdot 3^2+b\cdot 3+c\\ &&=&& a\cdot 9+b\cdot 3+c\\ \\ Q(-1|0): 0 &&=&& a\cdot(-1)^2+b\cdot (-1) +c\\ &&=&& a-b+c\\ \\ R(0|7): 7 &&=&& a\cdot0^2+b\cdot 0 +c\\ &&=&& c\\ \Rightarrow 7 &&=&&c \end{array} }

Setze den erhaltenen Wert für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} in die ersten beiden Gleichungen ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 1.: &&2 &&=&& a\cdot 9+b\cdot 3+7 &\mid -7\\ &\Leftrightarrow& -5 &&=&& a\cdot 9+b\cdot 3\\ \\ 2.: &&0 &&=&& a-b+7 &\mid -7\\ &\Leftrightarrow& -7 &&=&& a-b \end{array} }

Einsetzungsverfahren:

Stelle eine der beiden Gleichungen, z.B. die zweite, nach einer Variable um, z.B. nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 2.: &&-7 &&=&& a-b &\mid +b\\ &\Leftrightarrow& -7+b &&=&& a \end{array} }

Setze nun Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -7+b} in der anderen Gleichung für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} ein und stelle nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} um:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 1.: &&-5 &&=&& a\cdot 9+b\cdot 3 &\mid a=-7+b\\ &\Leftrightarrow& -5 &&=&& (-7+b)\cdot 9+b\cdot 3\\ &\Leftrightarrow& -5 &&=&& -63+b\cdot 9+b\cdot 3\\ &\Leftrightarrow& -5 &&=&& -63+12\cdot b &\mid +63\\ &\Leftrightarrow& 58 &&=&& 12\cdot b &\mid \div 12\\ &\Leftrightarrow& \frac{29}{6} &&=&& b\\ \end{array} }

Setze nun den Wert für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} in eine der Gleichungen ein, z.B. in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -7=a-b} , und stelle nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} um:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&-7 &&=&& a-b &\mid b=\frac{29}{6}\\ &\Leftrightarrow& -7 &&=&& a-\frac{29}{6} &\mid +\frac{29}{6}\\ &\Leftrightarrow& -\frac{13}{6} &&=&& a\\ \end{array} }

Somit ergibt sich: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=-\frac{13}{6}\cdot x^2+\frac{29}{6}\cdot x+7} .

(du könntest natürlich auch das Gleichsetzungsverfahren nutzen, oder das LGS mit dem Additionsverfahren lösen)

b)* Wie lautet die Funktionsgleichung zu den Punkten $P(4|3),Q(6|14)$ und $R(9|-4)$ ?

Die Normalform hat die Funktionsgleichung

g(x)=a\cdot x^{2}+b\cdot x+c

. Überlege dir wie du die Punkte in diese Funktion einfügen kannst.

Setze die Punkte jeweils einzeln in die Funktionsgleichung ein (den ersten Wert für das

x

und den zweiten Wert für das

y

). Du hast nun drei verschiedene Gleichungen. Überlege dir wie du dieses lineare Gleichungssystem (LGS) lösen kannst (evtl. hast du hier bereits einen Wert für

c

den du in die anderen Gleichungen einsetzten kannst).

Löse das LGS am besten mit dem Additionsverfahren. Du musst nun die Gleichungen so von einander subtrahieren oder addieren, sodass eine der Variablen dabei wegfallen. Dafür musst du zuerst dafür sorgen, sodass die Vorfaktoren dieser Variablen in beiden Gleichungen identisch sind. Hast du nun nur noch eine Variable in der entstandenen Gleichung kannst du nach dieser Variablen auflösen. Hast du noch zwei Variablen musst du erneut eine der Gleichungen mit einer anderen verrechnen um eine weitere Gleichung mit den beiden Variablen zu erhalten. Diese beiden musst du abermals so verrechnen, dass eine der beiden Variablen wegfällt.

Die ausgerechnete Variable kannst du nun in eine der Gleichungen einsetzen wo noch eine weitere Variable vorkommt. Jetzt kannst du erneut umstellen und die zweite Variable berechnen. Wiederhole das Verfahren, falls du

c

noch berechnen musst.

$g(x)=a\cdot x^{2}+b\cdot x+c$

Setze die Punkte $P,Q$ und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R} in die allgemeine Gleichung ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} P(4|3): 3 &&=&& a\cdot 4^2+b\cdot 4+c\\ &&=&& a\cdot 16+b\cdot 4+c\\ \\ Q(6|14): 14 &&=&& a\cdot 6^2+b\cdot 6 +c\\ &&=&& a\cdot 36+b\cdot 6+c\\ \\ R(9|-4): -4 &&=&& a\cdot 9^2+b\cdot 9 +c\\ &&=&& a\cdot 81+b\cdot 9+c\\ \end{array} }

Subtrahiere nun die Gleichungen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3=a\cdot 16+b\cdot 4+c} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 14=a\cdot 36+b\cdot 6+c} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&1.: 3 &&=&& a\cdot 16+b\cdot 4+c\\ &&2.: 14 &&=&& a\cdot 36+b\cdot 6+c\\ \\ &&1. - 2.:\\ &&3-14 &&=&& (16-36)\cdot a+ (4-6)\cdot b\\ &\Leftrightarrow& -11 &&=&& -20\cdot a-2\cdot b \end{array} }

Subtrahiere nun die Gleichungen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 14=a\cdot 36+b\cdot 6+c} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -4=a\cdot 81+b\cdot 9+c} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&2.: 14 &&=&& a\cdot 36+b\cdot 6+c\\ &&3.: -4 &&=&& a\cdot 81+b\cdot 9+c\\ \\ &&2. - 3.:\\ &&14-(-4) &&=&& (36-81)\cdot a+ (6-9)\cdot b\\ &\Leftrightarrow& 18 &&=&& -45\cdot a-3\cdot b \end{array} }

Bringe den Vorfaktor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} der beiden erhaltenen Gleichungen auf den selben Wert, z.B. auf Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 6} , indem du die erste Gleichung mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} und die zweite mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2} multiplizierst:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&-11\cdot 3 &&=&& -20\cdot 3\cdot a-2\cdot 3 \cdot b\\ &\Leftrightarrow& -33 &&=&& -60\cdot a-6\cdot b\\ \\ &&18\cdot 2 &&=&& -45\cdot 2\cdot a-3\cdot 2 \cdot b\\ &\Leftrightarrow& 36 &&=&& -90\cdot a-6\cdot b \end{array} }

Subtrahiere nun die Gleichungen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -33=-60\cdot a-6\cdot b} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 36=-90\cdot a-6\cdot b} und stelle nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} um:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&1.: -33 &&=&& -60\cdot a-6\cdot b\\ &&2.: 36 &&=&& -90\cdot a-6\cdot b\\ \\ &&1.- 2.:\\ &&-33-36 &&=&& (-60-(-90))\cdot a\\ &\Leftrightarrow& -69 &&=&& 30\cdot a &\mid \div 30\\ &\Leftrightarrow& -2.3 &&=&& a \end{array} }

Setze nun Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} in eine der Gleichungen ohne Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} ein, z.B. in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -11=-20\cdot a-2\cdot b} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&-11 &&=&& -20\cdot (-2.3)-2\cdot b\\ &\Leftrightarrow& -11 &&=&& 46-2\cdot b &\mid -46\\ &\Leftrightarrow& -57 &&=&& -2\cdot b &\mid \div (-2)\\ &\Leftrightarrow& 28.5 &&=&& b \end{array} }

Setze nun Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} in eine der Gleichungen mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} ein, z.B. in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3=a\cdot 16+b\cdot 4+c} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&3 &&=&& -2.3\cdot 16+28.5\cdot 4+c\\ &\Leftrightarrow& 3 &&=&& 77.2+c &\mid -77.2\\ &\Leftrightarrow& -74.2 &&=&& c \end{array} }

Somit ergibt sich: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x)=-2.3\cdot x^2+28.5\cdot x-74.2} .

Zusammenfassung zur Normalform

Die allgemeine Normalform lautet Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot x^2+b\cdot x+c} .
Der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} ist der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achsenabschnitt.
Der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} wird als Streckungsfaktor bezeichnet.
- Ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a>1} wird die Funktion gestreckt, ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<1} wird die Funktion gestaucht.
- Ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} positiv so ist die Parabel nach oben geöffnet, ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ so ist sie nach unten geöffnet.
- Wenn man den Streckungsfaktor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} zum zeichnen nutzen möchte, geht man vom Scheitelpunkt aus um eine Einheit nach links oder rechts und dann um Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} Einheiten nach oben (falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ ist nach unten). Falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<1} ist, oder generell ein Bruch ist, kann dies manchmal schwierig sein. Hierfür kann man die Normalparabel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^2} betrachten. Sinnvoll ist es nun den Nenner einzusetzen. Die erhaltene Zahl muss man nun mit dem Bruch multiplizieren. Man geht nun vom Scheitelpunkt um die eingesetzte Zahl nach links oder rechts und um die am Ende erhaltene Zahl nach oben, oder nach unten falls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} negativ ist.
Hat man drei Punkte gegeben und soll die zugehörige Funktionsgleichung aufstellen, so nimmt man sich die allgemeine Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot x^2+b\cdot x+c} . Hier setzt man alle drei Punkte jeweils für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} ein und erhält so drei Gleichungen. Nun löst man das lineare Gleichungssystem mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren.
Man gelangt von der Normalform (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot x^2+b\cdot x+c} ) zur Scheitelpunktform (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot (x-d)^2+e} ) mittels Quadratischer Ergänzung.
Man gelangt von der Scheitelpunktform (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot (x-d)^2+e} ) zur Normalform (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a\cdot x^2+b\cdot x+c} ) durch Ausmultiplizieren der Klammer.

Nullstellen

Eine Parabel kann entweder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2, 1} oder keine Nullstellen besitzen.

Sie hat Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2} Nullstellen, falls:
- sie nach oben geöffnet ist und ihr Scheitelpunkt einen negativen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert (kleiner als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} ) hat.
- sie nach unten geöffnet ist und ihr Scheitelpunkt einen positiven Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert (größer als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} ) hat.
Sie hat Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1} Nullstelle, falls ihr Scheitelpunkt den Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} hat (also die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse berührt).
Sie hat keine Nullstellen, falls:
- sie nach oben geöffnet ist und ihr Scheitelpunkt einen positiven Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert (größer als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} ) hat.
- sie nach unten geöffnet ist und ihr Scheitelpunkt einen negativen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert (kleiner als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} ) hat.

Entdecke!

Verändere die Parabel mit Hilfe der Schieberegler und beobachte die Nullstellen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_1} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_2} . Wann sind sie unterschiedlich, wann gleich und wann nicht vorhanden?

Im folgenden Abschnitt werden die verschiedenen Methoden zur Nullstellenberechnung wiederholt.

Methode 1: Wurzelziehen

Gegeben sei eine Gleichung der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=a\cdot x^2-c} , z.B. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=3\cdot x^2-27} .

Bei dieser Form ist die Bedingungen fürs Wurzelziehen erfüllt: Es gibt keinen Term der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b\cdot x} .

Nun muss noch umgeformt werden:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0 &&=&& a\cdot x^2-c &\mid \text{bringe c auf die andere Seite, also +c}\\ &\Leftrightarrow& c &&=&& a\cdot x^2 &\mid \text{teile durch a, damit der Vorfaktor von dem x² zu 1 wird}\\ &\Leftrightarrow& \frac{c}{a} &&=&& x^2 &\mid \text{ziehe nun die Wurzel, beachte dass die Zahl dafür positiv sein muss, und dass du zwei Ergebnisse hast}\\ &\Leftrightarrow& \pm \sqrt{\frac{c}{a}} &&=&& \sqrt{x^2}\\ \\ &\Rightarrow& x_1 &&=&& \sqrt{\frac{c}{a}}\\ &&x_2 &&=&& -\sqrt{\frac{c}{a}} \end{array} }

Als Beispiel:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0 &&=&& 3\cdot x^2-27 &\mid +27\\ &\Leftrightarrow& 27 &&=&& 3\cdot x^2 &\mid \div 3\\ &\Leftrightarrow& \frac{27}{3} &&=&& x^2 &\mid \sqrt{}\\ &\Leftrightarrow& \pm \sqrt{9} &&=&& \sqrt{x^2}\\ \\ &\Rightarrow& x_1 &&=&& 3\\ &&x_2 &&=&& -3 \end{array} }

Methode 2: Ausklammern

Gegeben sei eine Gleichung der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=a\cdot x^2+b\cdot x} , z.B. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=4\cdot x^2+8\cdot x} .

Bei dieser Form ist die Bedingungen fürs Ausklammern erfüllt: Es gibt keinen Term der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} , also keine Zahl ohne ein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} .

Nun muss noch umgeformt werden:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0 &&=&& a\cdot x^2+b\cdot x &\mid \text{teile durch a, damit der Vorfaktor von dem x² zu 1 wird}\\ &\Leftrightarrow& 0 &&=&& x^2+\frac{b}{a} \cdot x &\mid \text{klammere x aus}\\ &\Leftrightarrow& 0 &&=&& x\cdot (x+\frac{b}{a}) &\mid \text{dieses Produkt ist genau dann 0 wenn einer der beiden Faktoren 0 ist}\\ \\ &\Rightarrow& x &&=&& 0\\ \text{oder} &&x+\frac{b}{a}&&=&& 0 &\mid -\frac{b}{a}\\ &\Leftrightarrow& x &&=&& -\frac{b}{a}\\ \\ &\Rightarrow& x_1 &&=&& 0\\ &&x_2 &&=&& -\frac{b}{a} \end{array} }

Als Beispiel:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0 &&=&& 4\cdot x^2+8\cdot x &\mid \div 4\\ &\Leftrightarrow& 0 &&=&& x^2+\frac{8}{4} \cdot x &\mid \text{klammere x aus}\\ &\Leftrightarrow& 0 &&=&& x\cdot (x+2) &\mid \text{dieses Produkt ist genau dann 0 wenn einer der beiden Faktoren 0 ist}\\ \\ &\Rightarrow& x &&=&& 0\\ \text{oder} &&x+2&&=&& 0 &\mid -2\\ &\Leftrightarrow& x &&=&& -2\\ \\ &\Rightarrow& x_1 &&=&& 0\\ &&x_2 &&=&& -2 \end{array} }

Methode 3: p-q Formel

Gegeben sei eine Gleichung der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=a\cdot x^2+b\cdot x+c} , z.B. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=2\cdot x^2+8\cdot x+14} .

Bei dieser Form muss man entweder die p-q Formel (oder quadratische Ergänzung) anwenden.

Es muss umgeformt werden:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0 &&=&& a\cdot x^2+b\cdot x +c&\mid \text{teile durch a, damit der Vorfaktor von dem x² zu 1 wird}\\ &\Leftrightarrow& 0 &&=&& x^2+\frac{b}{a} \cdot x+\frac{c}{a} &\mid \text{setze in die pq-Formel ein}\\ &&x_{1/2} &&=&& -\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} &\mid p=+\frac{b}{a}, q=+\frac{c}{a}\\ &\Rightarrow& x_{1/2} &&=&& -\frac{b}{a\cdot 2}\pm \sqrt{(\frac{b}{a\cdot 2})^2-\frac{c}{a}}\\ \\ &\Rightarrow& x_1 &&=&& -\frac{b}{a\cdot 2}+ \sqrt{(\frac{b}{a\cdot 2})^2-\frac{c}{a}}\\ &&x_2 &&=&& \frac{b}{a\cdot 2}- \sqrt{(\frac{b}{a\cdot 2})^2-\frac{c}{a}} \end{array} }

Als Beispiel:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0 &&=&& 2\cdot x^2+16\cdot x +14&\mid \div 2\\ &\Leftrightarrow& 0 &&=&& x^2+\frac{16}{2} \cdot x+\frac{14}{2} &\mid \text{setze in die pq-Formel ein}\\ &&x_{1/2} &&=&& -\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} &\mid p=+\frac{16}{2}=8, q=+\frac{14}{2}=7\\ &\Rightarrow& x_{1/2} &&=&& -\frac{8}{2}\pm \sqrt{(\frac{8}{2})^2-7}\\ && &&=&& -4\pm \sqrt{4^2-7}\\ && &&=&& -4\pm \sqrt{16-7}\\ && &&=&& -4\pm \sqrt{9}\\ && &&=&& -4\pm 3\\ \\ &\Rightarrow& x_1 &&=&& -1\\ &&x_2 &&=&& -7 \end{array} }

12. Erkennen der schnellsten Methode zum Nullstellen berechnen.

Ordne die Gleichungen der Methode zu, mit der man die Nullstellen am schnellsten berechnen kann.

Wurzelziehen kann man anwenden wenn nur die Terme der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\cdot x^2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} vorkommen also kein Term mit einem Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} vorhanden ist. Hierzu zählen natürlich auch die Gleichungen wo zweimal ein Term mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^2} vorkommt. Passe auch auf wenn auf beiden Seiten der gleiche Term mit einem Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} vorkommt, kürzt sich dieser weg.

Ausklammern kann man anwenden wenn nur die Terme der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\cdot x^2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b\cdot x} vorkommen, also keine Zahl ohne ein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} vorhanden ist. Hierzu zählen natürlich auch die Gleichungen wo zweimal ein Term mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} vorkommt. Passe auch auf wenn auf beiden Seiten die gleiche Zahl ohne ein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} vorkommt, kürzt sich diese weg.

Die pq-Formel muss man anwenden wenn alle Termformen vorkommen, also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\cdot x^2, b\cdot x} und

c

. Pass hier allerdings auf wenn auf beiden Seiten der gleiche Term mit einem

x

, oder die gleiche Zahl ohne ein

x

vorkommt, kürzen sich dieser weg.

13. Nullstellen berechnen.

Löse die folgenden Gleichungen mit der jeweils schnellsten Methode.

a) $-6={\frac {3}{4}}\cdot x^{2}-9$

b) $4\cdot x^{2}=8\cdot x$

c) ${\frac {1}{3}}\cdot x^{2}-2\cdot x=8$

Mache dir klar welche Methode du jeweils anwenden kannst. Falls du dir unsicher bist scrolle hoch zu den Erklärungen der Methoden.

Überlege dir wie du die Gleichungen umstellen musst um die passende Form zu erhalten. Beachte ob ein Vorfaktor vor dem

x^{2}

steht und bringe ihn auf

1

.

Da hier kein Term der Form $b\cdot x$ vorkommt, kann die Methode Wurzelziehen angewandt werden:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&-6 &&=&& \frac{3}{4}\cdot x^2-9 &\mid +9\\ &\Leftrightarrow& 3 &&=&& \frac{3}{4}\cdot x^2 &\mid \cdot \frac{4}{3}\\ &\Leftrightarrow& \frac{3\cdot 4}{3} &&=&& x^2 &\mid \sqrt{}\\ &\Leftrightarrow& \pm \sqrt{4} &&=&& \sqrt{x^2}\\ \\ &\Rightarrow& x_1 &&=&& 2\\ &&x_2 &&=&& -2 \end{array} }

Da hier kein Term der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} vorkommt, also keine Zahl ohne ein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} , kann die Methode Ausklammern angewandt werden:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&4\cdot x^2 &&=&&8\cdot x &\mid \div 4\\ &\Leftrightarrow& x^2 &&=&& \frac{8}{4}\cdot x &\mid -\frac{8}{4}\cdot x\\ &\Leftrightarrow& x^2-2\cdot x &&=&& 0 &\mid \text{klammere x aus}\\ &\Leftrightarrow& x\cdot (x-2) &&=&&0 &\mid \text{dieses Produkt ist genau dann 0 wenn einer der beiden Faktoren 0 ist}\\ \\ &\Rightarrow& x &&=&& 0\\ \text{oder} &&x-2&&=&& 0 &\mid +2\\ &\Leftrightarrow& x &&=&& 2\\ \\ &\Rightarrow& x_1 &&=&& 0\\ &&x_2 &&=&& 2 \end{array} }

Da hier alle Termformen (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^2, b\cdot x, c} ) vorhanden sind muss die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle pq} -Formel angewandt werden:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&\frac{1}{3}\cdot x^2-2\cdot x &&=&& 8 &\mid -8\\ &\Leftrightarrow& \frac{1}{3}\cdot x^2-2\cdot x-8 &&=&& 0 &\mid \cdot 3\\ &\Leftrightarrow& x^2-3\cdot 2\cdot x-3\cdot 8 &&=&& 0 &\mid \text{setzte in die pq-Formel ein}\\ &&x_{1/2} &&=&& -\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} &\mid p=-3\cdot 2=-6, q=-3\cdot 8=-24\\ &\Rightarrow& x_{1/2} &&=&& -\frac{-6}{2}\pm \sqrt{(\frac{6}{2})^2-(-24)}\\ && &&=&& 3\pm \sqrt{3^2+24}\\ && &&=&& 3\pm \sqrt{9+24}\\ && &&=&& 3\pm \sqrt{33}\\ \\ &\Rightarrow& x_1 &&=&& 3+ \sqrt{33}\\ &&x_2 &&=&& 3- \sqrt{33} \end{array} }

14. Ordne zu.

Ordne den Funktionsgleichungen die zugehörigen Nullstellen zu. Berechne diese dafür in deinem Heft.

15. Baseball

Baseball ist eine der beliebtesten Sportarten der Welt. Beim Wurf erreicht der Ball Geschwindigkeiten bis zu Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 160km/h} . Wenn der Schlagmann den Ball richtig trifft, kann dieser über die Tribüne hinweg aus dem Stadion fliegen. Ein bestimmter Schlag kann durch die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h(x)=-0.0075\cdot x^2+1.2\cdot x+1} beschrieben werden, wobei die horizontale Entfernung zum Schlagmann und die Höhe des Balls, jeweils in Meter angibt.

a) Wie weit fliegt der Ball? Überlege dir dafür wo der Ball geschlagen wird und wo er aufkommt.

Da wo der Ball geschlagen wird, ist er ja noch keinen Meter geflogen, dementsprechend ist der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert hier noch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} .

Da wo der Ball auf dem Boden aufkommt hat er keine Höhe mehr, weswegen der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} . Gesucht ist demnach eine Nullstelle.

Setze die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h(x)=0} und berechne die Nullstellen. Du erhältst zwei. Überlege die nun welcher Wert mehr Sinn macht. Da der Abschlagpunkt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=0} ist, ist die Nullstelle die Entfernung die der Ball fliegt.

Setze die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h(x)=0} : Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -0.0075\cdot x^2+1.2\cdot x+1=0} .

Um diese Gleichung zu lösen muss die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p-q} Formel verwendet werden.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&0.0075\cdot x^2+1.2\cdot x+1 &&=&& 0 &\mid \div (-0.0075)\\ &\Leftrightarrow& x^2+\frac{1.2}{-0.0075}\cdot x +\frac{1}{-0.0075} &&=&& 0 &\mid \text{setzte in die pq-Formel ein}\\ &&x_{1/2} &&=&& -\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} &\mid p=+\frac{1.2}{-0.0075}=-160, q=+\frac{1}{-0.0075}=-\frac{400}{3}\\ &\Rightarrow& x_{1/2} &&=&& -\frac{-160}{2}\pm \sqrt{(\frac{160}{2})^2-(-\frac{400}{3})}\\ && &&=&& 80\pm \sqrt{80^2+\frac{400}{3}}\\ && &&=&& 80\pm \sqrt{6400+\frac{400}{3}}\\ && &&=&& 80\pm \sqrt{\frac{19600}{3}}\\ \\ &\Rightarrow& x_1 &&=&& 80+ \sqrt{\frac{19600}{3}}\approx 160.83\\ &&x_2 &&=&& 80- \sqrt{\frac{19600}{3}}\approx -0.83 \end{array} }

Da der Ball bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=0} geschlagen wird und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} die horizontale Flugweite angibt macht ein negativer Wert keinen sinn, weswegen der Ball demnach ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 160.83} Meter weit fliegt.

b) In einer Entfernung von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} Metern steht ein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,83} Meter großer Spieler. Dieser kann einen Ball aus ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} Metern Höhe fangen. Würde es ihm gelingen den Ball mit der obigen Flugkurve zu fangen?

Du musst berechnen wie hoch der Ball nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} Metern ist. Überlege dir dafür wo du die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} in die Gleichung einsetzen musst.

Setzte die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} ein, da der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert ja die horizontale Entfernung zum Abschlagpunkt angibt.

Gesucht ist die Höhe des Balls nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} Metern. Daher setzten wir die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} ein, da der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert ja die horizontale Entfernung zum Abschlagpunkt angibt:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} h(153) &&=&& -0.0075\cdot 153^2+1.2\cdot 153+1\\ &&=&& 9.03 \end{array} }

Der Ball ist also nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 153} Metern noch über Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 9} Meter hoch, weswegen der Spieler, der einen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} Meter hohen Ball fangen kann, an diesen nicht drankommt.

Anwendungsaufgaben

Bei den Anwendungsaufgaben zu quadratischen Funktionen handelt es sich in der Regel um eine Optimierungsaufgabe oder um das Lösen eines Sachzusammenhanges.

Optimierungsaufgaben

Bei Optimierungsaufgaben wird in der Regel danach gefragt unter welchen Bedingungen ein Wert maximal oder minimal wird. Da eine quadratische Funktion als Funktionsgraphen eine Parabel darstellt, ist der höchste (bei negativer Steigung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<0} ) bzw. tiefste (bei positiver Steigung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a>0} ) Punkt der Scheitelpunkt. Hier ist der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert der Funktion also maximal oder minimal. Dementsprechend muss die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achse den Wert beschreiben der maximal oder minimal werden soll.

Ist zum Beispiel bei einer vorgegebenen Länge (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 20m} ) Zaun der maximale Flächeninhalt gesucht, so muss auf der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achse der Flächeninhalt eingetragen werden.

Die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse muss dabei eine der Bedingungen beschreiben, die man verändern darf.

Zum Beispiel die Länge von einer Seite, diese setzt man dann als Variable Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} .

Vorgehen:

Schreibe dir auf was gesucht ist.
- z.B. maximaler Flächeninhalt.
Schreibe dir auf was gegeben ist.
- z.B. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 20m} Zaun zum einzäunen eines Rechtecks.
Notiere dir Formeln die du zu den gegebenen Größen weißt.
- Um den Flächeninhalt eines Rechtecks zu berechnen brauche ich die Formel: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A=a\cdot b} .
- Da ich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 20m} Zaun zur Verfügung habe, hat der Umfang meines Rechtecks den Wert Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 20} , also: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U=2\cdot a + 2\cdot b=20} .
Mache dir klar welcher Wert der ist, welcher in der quadratischen Funktion auf der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achse eingetragen sein muss.
- Da der Flächeninhalt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} maximiert werden soll gehört dieser auf die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achse. Da der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert vom Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert abhängt schreiben wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A(x)} .
Entscheide dich welche Bedingung du als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} setzen möchtest und stelle die andere Bedingung in Abhängigkeit von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} dar.
- Wir können uns zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} entscheiden. Wir setzen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} als Variable Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A(x)=x\cdot b} . Da uns das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} hier noch stört, müssen wir diese in Abhängigkeit von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} schreiben indem wir die zweite Formel umformen:
  
  Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&20 &&=&& 2\cdot x + 2\cdot b &\mid -2\cdot x\\ &\Leftrightarrow& 20-2\cdot x &&=&& 2\cdot b &\mid \div 2\\ &\Leftrightarrow& 10-x &&=&& b \end{array} }
  
  Nun können wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A(x)=x\cdot b} ersetzten:
  
  Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} A(x) &&=&& x\cdot b &\mid b=10-x\\ &&=&& x\cdot (10-x)\\ &&=&& 10\cdot x-x^2 \end{array} }
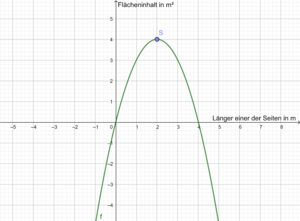
Forme in die Scheitelpunktform um.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} A(x) &&=&& -x^210\cdot x\\ &&=&& -(x-2\cdot 5\cdot x+5^2-5^2)\\ &&=&& -((x-5)^2-5^2)\\ &&=&&-(x-5)^2+25 \end{array} }
Lese den Scheitelpunkt ab und interpretiere ihn.
- Der Scheitelpunkt liegt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(5|25)} . Der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert gibt den Flächeninhalt an, weswegen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 25m^2} der maximale Flächeninhalt ist. Dieser wird erreicht bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=5} , also wenn die Seitenlänge von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=5m} beträgt. Da
  
  Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 20 &&=&& 2\cdot a + 2\cdot b\\ &&=&& 2\cdot 5 + 2\cdot b\\ &&=&& 10 + 2\cdot b \end{array} }
  
  gelten muss erhalten wir durch umformen für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} eine Länge von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 5m} .

16. Das Gemüsebeet.

Lina wollte schon immer ein Gemüsebeet in ihrem Garten haben. Da sie viel Wert auf das Aussehen legt hat sie sich als Zaun für einen Staketenzaun entschieden. Da dieser allerdings sehr teuer ist hat sie davon nur Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16} Meter gekauft.

a) Wie groß kann ihr Beet maximal werden?

Überlege dir was maximiert werden soll und welche Formeln du zu den gegebenen und gesuchten Größen kennst.

Der maximale Flächeninhalt ist gesucht und du brauchst die Formeln:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 1. A &&=&& a \cdot b\\ 2. U &&=&& 2\cdot a+2\cdot b &&=&& 16. \end{array} }

Stelle nun die Formel zum Umfang nach einer der beiden Variablen um und setzte dies dann für die Variable in der Formel für den Flächeninhalt ein.

Bestimme nun den Scheitelpunkt. Der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert ist der Wert des maximalen Flächeninhaltes und der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert ist die Länge der einen Seite.

Gesucht ist der maximale Flächeninhalt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16m} Umfang. Wie haben also die Formeln:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 1.: U &&=&& 2\cdot a+2\cdot b &&=&& 16\\ 2.: A &&=&& a\cdot b \end{array} }

Auf der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Achse muss nachher der Flächeninhalt eingetragen sein, da wir von diesem das Maximum suchen. Wie müssen also eine quadratische Funktion der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A(x)} aufstellen. Unsere Variablen sind dabei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} . Wir formen nun die Umfangsformel nach einer der beiden Variablen um, zum Beispiel nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} :

${\begin{array}{rlll}&&2\cdot a+2\cdot b&&=&&16&\mid -2\cdot b\\&\Leftrightarrow &2\cdot a&&=&&16-2\cdot b&\mid \div 2\\&\Leftrightarrow &a&&=&&8-b\end{array}}$

Den Wert den wir nun für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} erhalten haben können wir in die Formel für den Flächeninhalt einsetzten. Wir können uns entscheiden ob wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} setzten oder einfach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A(b)} schreiben:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&A &&=&& a\cdot b &\mid a=8-b\\ &\Leftrightarrow& A(b) &&=&& (8-b)\cdot b \\ && &&=&& -b^2+8b\\ && &&=&& -(b+4)^2+16\\ &\Rightarrow& SP &&=&& (-4|16) \end{array} }

Somit müssen die Seiten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 4m} lang sein, um den maximalen Flächeninhalt von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16m^2} zu erreichen.

b)* Um ihr Beet etwas größer zu bekommen möchte sie eine Wand des Gartenhäuschen mit einbauen, so spart sie immerhin Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3} Meter Zaun. Sie hat gelesen, dass man für sechs verschiedene Gemüsesorten mindestens ein Beet von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 20m^2} haben sollte. Kann Lina sechs verschiedene Gemüsesorten anbauen?

Überlege dir welchen Einfluss das Gartenhäuschen auf die Gleichung des Umfanges hat.

Normal lautet die Formel für den Umfang Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U=2\cdot a+2\cdot b=16} . Von der rechten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} Seite fallen jetzt allerdings Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3m} weg, die nicht mit umzäunt werden müssen. Daher gilt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U=2\cdot a+b+b-3=16}

Stelle nun die Umfangsgleichung wieder nach einer Variablen um und verfahre wie in a).

Gesucht ist der maximale Flächeninhalt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16m} Umfang und dem einbauen einer Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3m} langen Mauer. Wie haben also die Formeln:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 1.: U &&=&& 2\cdot a+b+b-3 &&=&& 16\\ &&\Leftrightarrow&& 2\cdot a+2\cdot b -3 &&=&& 16 &\mid +3\\ &&\Leftrightarrow&& 2\cdot a+2\cdot b &&=&& 19\\ 2.: A &&=&& a\cdot b \end{array} }

Wir haben hier also lediglich den Unterschied, dass wir einen Umfang von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 19m} statt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16m} haben:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && 2\cdot a+2\cdot b &&=&& 19 &\mid -2\cdot b\\ &\Leftrightarrow& 2\cdot a &&=&& 19-2\cdot b &\mid \div 2\\ &\Leftrightarrow& a &&=&& 9.5-b \end{array} }

Einsetzten:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&A &&=&& a\cdot b &\mid a=9.5-b\\ &\Leftrightarrow& A(b) &&=&& (9.5-b)\cdot b \\ && &&=&& -b^2+9.5b\\ && &&=&& -(b+4.75)^2+\frac{361}{16}\\ &\Rightarrow& SP &&=&& (-4.75|\frac{361}{16}) \end{array} }

Somit müssen die Seiten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 4.75m} lang sein, um den maximalen Flächeninhalt von ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 22.56m^2} zu erreichen. Da Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 22.56m^2 > 20m^2} kann Lina auch sechs Gemüsesorten anpflanzen.

c)** Robin möchte Lina gerne helfen und für sie ein Frühbeet bauen, in welchem sie ihre Pflanzen heranzüchten kann. Dafür will er eine rechteckige Box bauen. Diese soll sowohl nach oben und nach unten geöffnet sein, es geht also nur um die Wände. Insgesamt hat Robin Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 30m^2} Holz gekauft. Die Höhe der Box soll Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1.5m} betragen. Robin möchte wissen wie er die anderen Seitenlängen wählen muss, um das maximale Volumen zu erhalten. (Du kannst annehmen, dass er keinen Verschnitt hat und die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 30m^3} ohne Verluste verbauen kann.)

Überlege dir was maximiert werden soll und welche Formeln du zu den gegebenen und gesuchten Größen kennst.

Das maximale Volumen ist gesucht und der Flächeninhalt der Mantelfläche und die Höhe sind gegeben.

Du brauchst die Formeln:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 1. V &&=&& a \cdot b\cdot c\\ 2. A &&=&& 2\cdot a\cdot b+2\cdot a\cdot c &&=&& 30. \end{array} }

(mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} als Höhe).Stelle nun die Formel zum Flächeninhalt nach einer der beiden Variablen um und setzte dies dann für die Variable in der Formel für das Volumen ein.

Bestimme nun den Scheitelpunkt. Der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert ist der Wert des maximalen Volumens und der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert ist die Länge der einen Seite. Berechne jetzt noch die Länge der anderen Seite.

Gesucht ist also das maximale Volumen bei einer Mantelfläche von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 30m^2} und einer Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1.5m} . Wir brauchen daher die Formeln:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} V &&=&& a\cdot b\cdot c &\mid \text{Formel für das Volumen}\\ A &&=&& a\cdot b\cdot 2+a\cdot c \cdot 2 &\mid \text{Formel für die Mantelfläche mit a als Höhe} \end{array} }

Da wir den Flächeninhalt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (30m^2)} und die Höhe Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1.5m)} gegeben haben können wir diese Werte jeweils einsetzten:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} V &&=&& 1.5\cdot b\cdot c &\mid \text{Formel für das Volumen mit der Höhe 1.5}\\ 30 &&=&& 1.5\cdot b\cdot 2+1.5\cdot c \cdot 2 &\mid \text{Formel für die Mantelfläche mit a als Höhe}\\ &&=&& 3\cdot b+3\cdot c \end{array} }

Als nächste müssen wir wie gewohnt umformen. Da diesmal das Volumen maximiert werden soll und wir als zusätzliche Formel den Flächeninhalt haben, müssen wir hier die Formel für den Flächeninhalt nach einer Variable umformen, z.b. nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&30 &&=&& 3\cdot b+3\cdot c &\mid -3\cdot c\\ &\Leftrightarrow& 30-3\cdot c &&=&& 3\cdot b &\mid \div 3\\ &\Leftrightarrow& 10-c &&=&& b \end{array} }

Diesen Wert setzen wir nun für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} in die Volumenformel ein:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} V(c) &&=&& 1.5\cdot b\cdot c &\mid b=10-c\\ &&=&& 1.5\cdot (10-c)\cdot c &\mid \text{ausrechnen}\\ &&=&& 15\cdot c-1.5\cdot c^2 \end{array} }

Somit haben wir nun eine Formel für das Volumen. Da dieses maximal werden soll müssen wir den Scheitelpunkt bestimmen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} V(c) &&=&& -1.5\cdot c^2+15\cdot c\\ &&=&& -1.5\cdot (c^2+10c)\\ &&=&& -1.5\cdot ((c^2+2\cdot 5 \cdot c+5^2)-5^2)\\ &&=&& -1.5\cdot ((c+5)^2-5^2)\\ &&=&& -1.5\cdot (c+5)^2+37.5 \end{array} }

Wir erhalten daher ein maximales Volumen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 37.5m^3} wenn Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c=5m} lang ist. Demnach muss Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b=10-c=10-5=5m} lang sein.

17. Pizzaladen**

Laura und Paul möchten zusammen einen Pizzaladen eröffnen. Vorher möchten sie die Produktion kalkulieren. Pro Tag können sie mit Miete, Stromkosten, Wasserkosten, etc. mit rund Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 500} € rechnen. Pro Pizza entstehen durch Material- und Lohnkosten nochmal rund Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10} €. Zusätzlich entstehen für die Produktion von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} Pizzen nochmals Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0.004\cdot x^2} €. Pro Pizza möchten sie Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 15} € nehmen. Zusätzlich müssen sie Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 40} % von ihrem Gewinn versteuern. Bei welcher Tagesanzahl von Pizzen wäre der verdienst maximal und wie hoch wäre dieser?

Überlege dir was maximiert werden soll und wie du die gegebene Größen in eine Funktion schreiben kannst.

Der maximale Gewinn nach Abzug der Steuern ist gesucht (Hinweis: Hier ist Zinssatzrechnung notwendig) ist gesucht. Die Fixkosten, die Kosten pro Stück und der verdienst sind gegeben. Diese müssen nun mit den richtigen Rechenzeichen in eine Funktion gebracht werden. Wichtig zu den steuern ist, dass hier nicht 40% wie bei Zinsen drauf gerechnet, sondern abgezogen werden.

Die Beträge die Kosten verursachen müssen ein Minus bekommen, da sie ja vom Gewinn abgezogen werden.

Bestimme nun den Scheitelpunkt. Der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} -Wert ist der Wert des maximalen Gewinns und der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Wert ist die Anzahl der Pizzen.

Da nur die Stückzahl der Pizzen variiert werden kann, setzen wir diese als unser Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} . Wir bringen nun alle Informationen in einer Gleichung zusammen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&-500 &\mid \text{Es fallen jeden Tag 500€ an die vom Gewinn abgezogen werden}\\ &&-500-10\cdot x &\mid \text{Zusätzlich fallen pro Pizza 10€ an}\\ &&-500-10\cdot x-0.004\cdot x^2 &\mid \text{Zusätzlich fallen 0.004x²€ für x Pizzen an}\\ &&-500-10\cdot x-0.004\cdot x^2+15\cdot x &\mid \text{Pro Pizza erhalten sie 15€}\\ &&(-500-10\cdot x-0.004\cdot x^2+15\cdot x)\cdot (1-0.4) &\mid \text{Von dem Gewinn werden nun 40 Prozent Steuern abgezogen, daher mal (1-0.4)}\\ f(x) &=& (-500-10\cdot x-0.004\cdot x^2+15\cdot x)\cdot (1-0.4) &\mid \text{Dies ist also unsere Funktion} \end{array} }

Wir haben nun also unsere Funktion gefunden. Diese können wir nun vereinfachen und da wieder das Maximum gesucht ist den Scheitelpunkt bestimmen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} f(x) &&=&& (-500-10\cdot x-0.004\cdot x^2+15\cdot x)\cdot (1-0.4) &\mid \text{vereinfachen}\\ &&=&& (-500+5\cdot x-0.004\cdot x^2)\cdot (1-0.4) &\mid \text{Klammer ausmultiplizieren}\\ &&=&& -500+5\cdot x-0.004\cdot x^2+200-2\cdot x+0.0016x^2 &\mid \text{vereinfachen}\\ &&=&& -300+3\cdot x-0.0024\cdot x^2 &\mid \text{-0.0024 ausklammern}\\ &&=&& -0.0024\cdot(125000-1250\cdot x+x^2) &\mid \text{quadratische Ergänzung}\\ &&=&& -0.0024\cdot((x^2-2\cdot 625\cdot x+625^2)-625^2+125000)\\ &&=&& -0.0024\cdot((x-625)^2-265625)\\ &&=&& -0.0024\cdot(x-625)^2-637.5 \end{array} }

Somit ist also der maximale Gewinn bei einer Produktion von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 625} Pizzen pro Tag gegeben. Der maximale Gewinn beträgt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 637.5} €.

Lösen eines Sachzusammenhangs

Bei Sachzusammenhangsaufagben wird in der Regel nach dem Wert einer bestimmten Variable gefragt. Diese Variable hat dabei einen Einfluss auf die gegebenen Größen. So ist zum Beispiel oft nach einem bestimmten Zinssatz gefragt, den man anhand von gegebenen Kontoständen ermitteln soll. Dafür muss man wissen in welcher Weise die gegebenen Größen von der Variablen abhängen.

Ist zum Beispiel der Kontostand zu Ende eines Jahres von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1000} Euro gegeben, werden dann die Jahreszinsen hinzugefügt, nochmal Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 150} Euro abgebucht und Anfang des Jahres darauf die Jahreszinsen nochmals ergänzt und dann der Kontostand Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 975} Euro gegeben, so ist in der Regel der Zinssatz Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} gesucht.

Hier ist in der Regel die gesuchte Variable die, welche man in der quadratischen Funktion als das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} setzt. Meistens stellt man durch die Bedingungen direkt eine Gleichung auf, welche man dann lösen muss (Nullstellenberechnung).

Hier wäre also unser Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} unser Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} .

Vorgehen:

Schreibe dir auf was gesucht ist.
- z.B. Zinssatz.
Schreibe dir auf was gegeben ist.
- z.B. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1000} Euro Ende Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2013} .
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2014} kommen Zinsen drauf und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 150} Euro werden abgezogen
- Anfang Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2015} kommen nochmal Zinsen drauf und man erhält Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 975} €
Notiere dir Formeln die du zu den gegebenen Größen weißt.
- Der Kontostand mit den Jahreszinsen berechnet man durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1000\cdot (1+p)} . (Wir behalten ja unseren Kontostand von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1000} Euro und bekommen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1000\cdot p} Euro noch zusätzlich, also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1000+1000\cdot p =1000\cdot (1+p)} ).
Bringe alle Größen in einer Formel unter.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &1000 &\mid \text{Kontostand 2013}\\ &1000\cdot (1+p) &\mid \text{Kontostand mit Zinsen}\\ &1000\cdot (1+p)-150 &\mid \text{Kontostand mit Zinsen und 150 Euro abgezogen}\\ &(1000\cdot (1+p)-150)\cdot (1+p) &\mid \text{Kontostand mit Zinsen, 150 Euro abgezogen und nächsten Zinsen}\\ &(1000\cdot (1+p)-150)\cdot (1+p)=975 &\mid \text{Kontostand mit Zinsen, 150 Euro abgezogen, nächsten Zinsen und Endbetrag} \end{array} }
Löse die erhaltene Gleichung.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&(1000\cdot (1+p)-150)\cdot (1+p) &&=&& 975 &\mid \text{multipliziere die innere Klammer aus}\\ &\Leftrightarrow& (1000+1000\cdot p-150)\cdot (1+p) &&=&& 975 &\mid \text{vereinfache}\\ &\Leftrightarrow& (850+1000\cdot p)\cdot (1+p) &&=&& 975 &\mid \text{multipliziere die Klammer aus}\\ &\Leftrightarrow& 850+1000\cdot p+850\cdot p+1000\cdot p^2 &&=&& 975 &\mid \text{vereinfache}\\ &\Leftrightarrow& 850+1850\cdot p+1000\cdot p^2 &&=&& 975 &\mid -975\\ &\Leftrightarrow& -125+1850\cdot p+1000\cdot p^2 &&=&& 0 &\mid \div 1000\\ &\Leftrightarrow& -0.125+1.85\cdot p+p^2 &&=&& 0 &\mid \text{pq-Formel, p=1.85 und q=-0.125}\\ &\Rightarrow& p_{1/2} &&=&& -\frac{1.85}{2} \pm \sqrt{(\frac{1.85}{2})^2-(-0.125)}\\ && &&=&& -0.925 \pm \sqrt{\frac{1369}{1600}+0.125}\\ && &&=&& -0.925 \pm \sqrt{\frac{1569}{1600}}\\ &\Rightarrow& p_1 &&=&& -0.925+\sqrt{\frac{1569}{1600}}\approx 0.07\\ &&p_2 &&=&& -0.925-\sqrt{\frac{1569}{1600}}\approx -1.18 \end{array} }
Interpretiere die Nullstellen im Sachzusammenhang und wähle die passende aus.
- Da Geld hinzugefügt und nicht abgezogen wird macht ein negativer Wert keinen Sinn, demnach ist unser gesuchter Zinssatz Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p\approx 0.07} . Als Prozentzahl also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0.07\cdot 100=7} %.

18. Kapitalanlage

Sören (14 Jahre alt) möchte sich mit 16 einen Roller kaufen um unabhängiger zu sein. Er hat bereits durch Geburtstage und Minijobs Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 490} € gespart. Die meisten Roller kosten um die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 550} €.

a) Er möchte nicht länger alles Geld beiseite legen müssen und überlegt, ob er das Geld einfach auf die Bank bringen könnte und durch die Zinsen in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2} Jahren sein Geld zusammen hätte. Wie hoch müsste dafür der Zinssatz sein?

Überlege dir was gegeben und was gesucht ist. Setzte die gesuchte Größe als deine Variable. Trage dann alle Informationen in einer Gleichung zusammen und löse sie.

Der Zinssatz ist ja gesucht, also ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} unsere Variable. Überlege dir, wie du den Kontostand nach einem Jahr mit den hinzugekommenen Zinsen berechnen kannst.

Den Kontostand nach einem Jahr berechnest du durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 490+490\cdot p} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 490\cdot (1+p)} . Überlege dir nun wie du das zweite Jahr mit einbringen kannst und was am Ende als Kontostand rauskommen soll. Wenn du eine Gleichung aufgestellt hast berechne Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} .

Für das zweite Jahr hast du ja nun den Kontostand Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 490\cdot (1+p)} . Von diesem Betrag erhältst du wieder Zinsen mit dem selben Zinssatz Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (490\cdot (1+p))\cdot (1+p)} . Sören braucht einen Kontostand von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 550} € um sich den Roller nach zwei Jahren leisten zu können.

Bringe die gegebenen Informationen in einer Gleichung unter:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 490 &\mid \text{Startguthaben}\\ 490\cdot (1+p) &\mid \text{Startguthaben und Jahreszinsen}\\ (490\cdot (1+p))\cdot (1+p) &\mid \text{Startguthaben und zweimal Jahreszinsen}\\ (490\cdot (1+p))\cdot (1+p)=550 &\mid \text{Startguthaben und zweimal Jahreszinsen und Endbetrag} \end{array} }

Löse die Gleichung:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && (490\cdot (1+p))\cdot (1+p) &&=&& 550 &\mid \text{multipliziere die innere Klammer aus}\\ &\Leftrightarrow& (490+490\cdot p)\cdot (1+p) &&=&& 550 &\mid \text{multipliziere die Klammer aus}\\ &\Leftrightarrow& 490+490\cdot p+490\cdot p+490\cdot p^2 &&=&& 550 &\mid \text{vereinfache}\\ &\Leftrightarrow& 490+980\cdot p+490\cdot p^2 &&=&& 550 &\mid -550\\ &\Leftrightarrow& -60+980\cdot p+490\cdot p^2 &&=&& 0 &\mid \div 490\\ &\Leftrightarrow& -\frac{6}{49}+2\cdot p+p^2 &&=&& 0 &\mid \text{pq-Formel}: p=2, q=-\frac{6}{49}\\ &\Rightarrow& p_{1/2} &&=&& -\frac{2}{2} \pm \sqrt{(\frac{2}{2})^2-(-\frac{6}{49})}\\ && &&=&& -1 \pm \sqrt{1+\frac{6}{49}}\\ && &&=&& -1 \pm \sqrt{\frac{55}{49}}\\ &\Rightarrow& p_1 &&=&& -1+\sqrt{\frac{55}{49}}\approx 0.06\\ && p_2 &&=&& -1-\sqrt{\frac{55}{49}}\approx -2.06 \end{array} }

Da auch hier Geld hinzukommen und nicht abgezogen werden soll, kann der negative Wert ausgeschlossen werden. Demnach ist der Zinssatz den Sören benötigen würde Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p\approx 0.06} , also ungefähr Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 6} %.

b)* Sören bringt sein Geld auf die Bank. Nach dem ersten Jahr Zinsen geht sein Handy kaputt und er muss von seinem ersparten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100} € abheben. Nachdem er ein weiteres mal Zinsen erhält, bekommt er von seinen Eltern zum Geburtstag einen Zuschuss von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 150} €. Den Roller kann er sich jetzt genau leisten. Wie hoch war der Zinssatz der Bank?

Überlege dir was gegeben und was gesucht ist. Setzte die gesuchte Größe als deine Variable. Trage dann alle Informationen in einer Gleichung zusammen und löse sie.

Wie in a) ist ja der Zinssatz gesucht, also ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} unsere Variable. Da es auch hier wieder um zwei Jahre geht, kannst du die Zinsen wie in a) berechnen. Du musst jetzt allerdings überlegen wo und wie du die weiteren gegebenen Größen mit in die Gleichung einbauen kannst.

Im ersten Jahr passiert nichts, also kannst du hier einfach wieder die Formel für die Zinsen nehmen. Dann werden allerdings Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100} € abgezogen. Dann erhält Sören erneut Zinsen, wieder mit dem selben Zinssatz Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} . Am Ende kriegt er noch zusätzlich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 150} € von seinen Eltern. Auch hier ist der Endkontostand dann wieder bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 550} €. Überlege dir wie du diese Informationen in eine Gleichung bringen kannst und berechne dann Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} .

Da im ersten Jahr nichts passiert hast du für das erste mal Zinsen wieder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 490\cdot (1+p)} . Von diesem Betrag werden dann allerdings Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100} € abgezogen, also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 490\cdot (1+p)-100} . Dann erhält Sören erneut Zinsen, wieder mit dem selben Zinssatz Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (490\cdot (1+p)-100)\cdot (1+p)} . Am Ende kriegt er noch zusätzlich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 150} € von seinen Eltern, alsoFehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (490\cdot (1+p)-100)\cdot (1+p)+150} . Auch hier ist der Endkontostand dann wieder bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 550} €.

Bringe die gegebenen Infos in eine Gleichung:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 490 &\mid \text{Startguthaben}\\ 490\cdot (1+p) &\mid \text{Startguthaben und Zinsen}\\ 490\cdot (1+p)-100 &\mid \text{Startguthaben und Zinsen abzüglich der Handykosten}\\ (490\cdot (1+p)-100)\cdot (1+p) &\mid \text{Startguthaben und Zinsen abzüglich der Handykosten und erneute Zinsen}\\ (490\cdot (1+p)-100)\cdot (1+p)+150 &\mid \text{Startguthaben und Zinsen abzüglich der Handykosten, erneute Zinsen und Zuschuss}\\ (490\cdot (1+p)-100)\cdot (1+p)+150=550 &\mid \text{Startguthaben und Zinsen abzüglich der Handykosten, erneute Zinsen, Zuschuss und Endbetrag} \end{array} }

Löse die Gleichung:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && (490\cdot (1+p)-100)\cdot (1+p)+150 &&=&& 550 &\mid \text{multipliziere die innere Klammer aus}\\ &\Leftrightarrow& (490+490\cdot p-100)\cdot (1+p)+150 &&=&& 550 &\mid \text{vereinfache}\\ &\Leftrightarrow& (390+490\cdot p)\cdot (1+p)+150 &&=&& 550 &\mid \text{multipliziere die Klammer aus}\\ &\Leftrightarrow& 390+490\cdot p+390\cdot p+490\cdot p^2+150 &&=&& 550 &\mid \text{vereinfache}\\ &\Leftrightarrow& 540+880\cdot p+490\cdot p^2 &&=&& 550 &\mid -550\\ &\Leftrightarrow& -10+880\cdot p+490\cdot p^2 &&=&& 0 &\mid \div 490\\ &\Leftrightarrow& -\frac{1}{49}+\frac{88}{49}\cdot p+p^2 &&=&& 0 &\mid \text{pq-Formel}: p=\frac{88}{49}, q=-\frac{1}{49}\\ &\Rightarrow& p_{1/2} &&=&& -\frac{88}{49\cdot 2} \pm \sqrt{(\frac{88}{49\cdot 2})^2-(-\frac{1}{49})}\\ && &&=&& -\frac{44}{49} \pm \sqrt{\frac{1936}{2401}+\frac{1}{49}}\\ && &&=&& -\frac{44}{49} \pm \sqrt{\frac{1985}{2401}}\\ &\Rightarrow& p_1 &&=&& -\frac{44}{49}+\sqrt{\frac{1985}{2401}}\approx 0.01\\ && p_2 &&=&& -\frac{44}{49}-\sqrt{\frac{1985}{2401}}\approx -1.81 \end{array} }

Da auch hier eine negative Zahl keinen Sinn macht, beträgt der Zinssatz Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p=0.01} , also in Prozent Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0.01\cdot 100=1} %.

19. Gartenplanung*

Katrin arbeitet in einem Gartenbaubetrieb. Sie soll eine rechteckige Fläche gestalten mit den Seitenlängen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 9m} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 12m} . Am inneren Rand des Rechteckes soll ein Weg verlaufen, der immer gleich breit bleibt und insgesamt die Hälfte der Fläche einnimmt. Wie breit muss der Weg dafür sein?

Überlege dir was gesucht und was gegeben ist. Kannst du die Größen mit Hilfe von bekannten Formeln in Beziehung setzten?

Die breite des Weges ist gesucht und die Längenangaben des gesamten Rechteckes sind gegeben. Zudem wissen wir, dass der Weg / bzw. das Beet jeweils die Hälfte der Fläche bedecken sollen. Die Fläche können wir durch die gegebenen Längen direkt berechnen. Schaue wie du den Flächeninhalt des Beetes in Abhängigkeit von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} berechnen kannst. (Du kannst natürlich auch mit dem Flächeninhalt des Weges rechnen, allerdings ist dieser etwas komplizierter zu berechnen).

Die Seitenlänge Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} des Beetes lässt sich berechnen durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 12-2\cdot c} und die von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 9-2\cdot c} . Somit ergibt sich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A=(12-2\cdot c)\cdot (9-2\cdot c)} . Dies muss nun gleich der Hälfte des gesamten Flächeninhaltes sein. Löse die erhaltene Gleichung nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} auf.

Wir wissen, dass wir insgesamt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 9m\cdot 12m=108m^2} Fläche zur Verfügung haben, wovon der Weg und das Beet jeweils die Hälfte einnehmen sollen. Seien Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} die Seitenlängen des Beetes und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} die Breite des Weges, dann ergibt sich:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} a &&=&& 12-2\cdot c\\ b &&=&& 9-2\cdot c\\ \Rightarrow A &&=&& a \cdot b &\mid \text{Flächeninhalt vom Beet}\\ &&=&& (12-2\cdot c)\cdot (9-2\cdot c) &\mid \text{a und b eingesetzt}\\ &&=&& 54 &\mid \text{soll die Hälfte von 108m² ergeben} \end{array} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (12-2\cdot c)\cdot (9-2\cdot c)=54} ist somit unsere Gleichung die wir lösen müssen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &&(12-2\cdot c)\cdot (9-2\cdot c) &&=&& 54 &\mid \text{Klammern ausrechnen}\\ &\Leftrightarrow& 108-18\cdot c-24\cdot c+4\cdot c^2 &&=&& 54 &\mid \text{vereinfachen}\\ &\Leftrightarrow& 108-42\cdot c+4\cdot c^2 &&=&& 54 &\mid -54\\ &\Leftrightarrow& 54-42\cdot c+4\cdot c^2 &&=&& 0 &\mid \div 4\\ &\Leftrightarrow& c^2-\frac{21}{2}\cdot c+\frac{27}{2} &&=&& 0 &\mid \text{pq-Formel}, p=-\frac{21}{2}, q=\frac{27}{2}\\ &\Rightarrow& c_{1/2} &&=&& -(-\frac{21}{2\cdot 2})\pm \sqrt{(\frac{21}{2\cdot 2})^2-\frac{27}{2}}\\ && &&=&& \frac{21}{4}\pm \sqrt{\frac{441}{16}-\frac{27}{2}}\\ && &&=&& \frac{21}{4}\pm \sqrt{\frac{225}{16}}\\ && &&=&& \frac{21}{4}\pm \frac{15}{4}\\ &\Rightarrow& c_1 &&=&& \frac{36}{4} &&=&& 9\\ && c_2 &&=&& \frac{6}{4} &&=&& 1.5 \end{array} }

Somit muss Katrin den Weg Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1.5m} breit machen, damit alle Anforderungen erfüllt sind.

Suche

Alles rund um Quadratische Funktionen

Inhaltsverzeichnis

Scheitelpunktform

Umwandlung Scheitelpunktform und Normalform

Die Normalform

Nullstellen

Anwendungsaufgaben

Navigation

Fächer

Hilfen

⧼advertisement⧽

Suche

Alles rund um Quadratische Funktionen

Scheitelpunktform

Umwandlung Scheitelpunktform und Normalform

Die Normalform

Nullstellen

Anwendungsaufgaben

Navigation

⧼advertisement⧽

⧼timis-pagehighlighted⧽

⧼timis-pagenamespaces⧽

⧼timis-pagetranslate⧽

Seitenwerkzeuge

Seitenwerkzeuge