Lernpfad 8a - Volumina und Flächen/Kreisumfang: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 61: | Zeile 61: | ||
Tastenkombination für die Kreiszahl π für Berechnungen mit dem Taschenrechner: | Tastenkombination für die Kreiszahl π für Berechnungen mit dem Taschenrechner: | ||
[[Datei: | [[Datei:Taschenrechnung pi.jpg|alternativtext=|ohne|mini|271x271px]] | ||
==<span class="brainy hdg-ruler-compasses fa-2x"></span> Übungen== | ==<span class="brainy hdg-ruler-compasses fa-2x"></span> Übungen== | ||
Version vom 23. Juni 2022, 08:20 Uhr
Erste Erkundungen
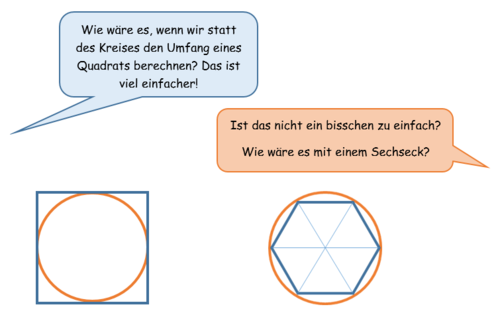
Jannis und Paula überlegen, wie sie den Umfang eines Kreises berechnen können.
Welche erste Abschätzung für den Kreisumfang lässt sich aus den beiden Vorgehensweisen erkennen? Kreuze alle richtigen Antwortmöglichkeiten an.
Der Umfang ist größer als (1x Durchmesser) (2x der Durchmesser) (3x der Durchmesser) (!4x der Durchmesser)
Der Umfang ist kleiner als (!1x der Durchmesser) (!2x der Durchmesser) (!3x der Durchmesser) (4x der Durchmesser)
Forscherauftrag
Kreise begegnen uns vielfach im Alltag. Suche dir mindestens fünf kreisrunde Gegenstände. Bestimme den Durchmesser und den Umfang dieser Gegenstände, indem du geeignete Messinstrumente verwendest (z.B. Lineal, Faden, Maßband).
Halte deine Ergebnisse in einer Tabelle in deinem Heft unter der Überschrift fest.
| Gegenstand | Durchmesser d (in cm) | Umfang U (in cm) |
|---|---|---|
| ... | ... | ... |
Betrachte die Messergebnisse in der Tabelle. Kannst du eine Regelmäßigkeit erkennen?
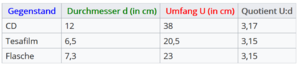
Untersuche, welcher Zusammenhang zwischen dem Durchmesser d und dem Umfang U des Kreises besteht. Notiere deine Vermutungen.Pia hat folgende Messergebnisse. Sie schaut sich das Verhältnis von Umfang und Durchmesser an und ergänzt ihre Tabelle.
Überprüfe deine Vermutung mithilfe des Applets. Du kannst die Genauigkeit deiner Messungen kontrollieren und weitere Daten sammeln. Sollte das Applet nicht richtig laden, klicke [1].

Der Kreisumfang
Der Umfang U eines Kreises ist ungefähr dreimal so groß wie sein Durchmesser d. Genauer beschreibt die Kreiszahl das Verhältnis zwischen dem Umfang und dem Durchmesser: Für einen Kreis mit dem Radius und dem Durchmesser gilt
Ergänze deinen Hefteintrag um eine Skizze und ein Beispiel..
Die Kreiszahl π
Beim Kreis ist das Verhältnis von Umfang U und Durchmesser d ist immer gleich.
Dieses Verhältnis wird Kreiszahl π genannt. = π = 3,141... Dieser Dezimalbruch endet nie. π ist also kein Element der rationalen Zahlen.
Dorfuchs hat die ersten 200 Nachkommastellen von π mit einer Fußballjonglage verbunden, schaus' dir an:
Und nun noch einige kurze Infos zur Kreiszahl π:
- eine der bekanntesten und sagenumwobensten Zahlen der Mathematik
- Ansätze ihrer Berechnung wurden schon im 17 Jahrhundert v. Chr. im Rechenbuch des Ahmes angedeutet
- mathematisch relativ genau als erstes von dem griechischen Mathematiker und Philosoph Archimedes im Jahr 250 v .Chr. bestimmt worden, mit 2 Dezimalstellen (3,14)
- Mittlerweile (2021) von Schweizer Forschern auf ca. 62,8 Billionen Dezimalstellen berechnet
- beschreibt das Verhältnis vom Umfang des Kreise zu seinem Durchmesser, welches bei allen Kreisen gleich ist:
π = = 3,14159...
- Ein Kreis mit dem Durchmesser 1 hat somit einen Umfang von π.
Tastenkombination für die Kreiszahl π für Berechnungen mit dem Taschenrechner:
Übungen
Berechne den Kreisumfang. Runde auf zwei Nachkommastellen.
- Der Radius des Kreises beträgt cm.
- Der Radius des Kreises beträgt mm.
- Der Radius des Kreises beträgt cm.
- Der Radius des Kreises beträgt m.
Lösungen:
Bestimme die Länge der Strecke, die ein Fahrrad mit einem 26-Zoll-Reifen bei einer Radumdrehung zurück legt.
Hinweis: 1 Zoll entspricht 2,54cmDer Raddurchmesser beträgt 26 Zoll und damit 66,04 cm. Es gilt .
Mit einer Umdrehung legt das Fahrrad 207,47 cm zurück.