Zentrische Streckung/Vierstreckensatz/3.Station

1. Station: Erster Vierstreckensatz - Schenkellösung - 2. Station: Erster Vierstreckensatz - Abschnittlösung - 3. Station: Zweiter Vierstreckensatz - 4. Station: Zusammenfassung - 5. Station: Übung

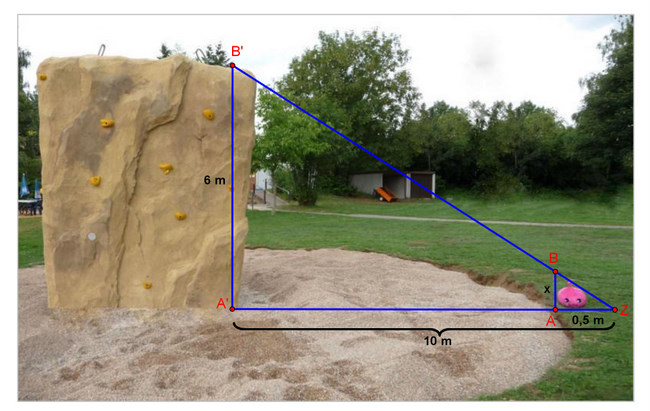
3. Station: Zweiter Vierstreckensatz

Früher wurden die Höhen von Pyramiden, Bäumen, Türmen usw. berechnet, indem man einen Stab lotrecht so aufstellte,

dass das Ende seines Schattens mit dem Ende des Schattens des Objektes zusammenfiel. Dabei wurde die Länge des Schattens

des Objektes und die Länge des Schattens vom Stab gemessen.

Wie du auf dem Bild sehen kannst, hat Panto einen Stab vergessen und sich selbst platziert. Panto weiß, dass die Kletterwand

6 m hoch ist, nur hat er mit zunehmendem Alter vergessen, wie groß er ist.

Hilf ihm, seine Größe herauszufinden:

Zunächst musst du wieder eine passende Formel zur Berechnung der gesuchten Strecke x herleiten! Setze wieder die richtige

Aussage in die passende Lücke ein:

$\overline{ZA'} =$ $\mid k\mid \cdot \overline{ZA}$ $\mathit{und}\$ $\overline{A'B'} =$ $\mid k\mid \cdot \overline{AB}$
Aufgelöst nach |k|:
$\mid k\mid =$ ${\overline{ZA'}\over\overline{ZA}}$ $\mathit{und}\$ $\mid k\mid$ $= {\overline{A'B'}\over\overline{AB}}$
Gleichsetzen:
${\overline{ZA'}\over\overline{ZA}} = {\overline{A'B'}\over\overline{AB}}$

Fantastisch! Du hast hier den zweiten Vierstreckensatz hergeleitet.

Dieser Satz sagt aus, dass sich die Streckenabschnitte auf den Parallelen wie die zugehörigen Streckenlängen (von Z ausgehend)

auf einer Geraden verhalten.

Trage hier deine Lösung mit Angabe der Einheit (m) ein!

${10\ m \over 0,5\ m} = {6\ m \over x}$
Umstellen, damit die gesuchte Länge links oben steht:
${x \over 6\ m} = {0,5\ m \over 10\ m}$
Berechne das Ergebnis mit dem Taschenrechner:
x = 0,3 m (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).