Mathematik-digital/Textaufgaben/Aus der Geometrie
- Wiederholung Gleichungen lösen
- Zahlenrätsel
- Altersrätsel
- Aus der Geometrie
- Verteilungsaufgaben
- Wissenstest
Einführung
Bei geometrischen Aufgaben ist es wichtig, dass du dir die entsprechenden Formeln für Umfang, Flächeninhalt, etc. wieder ins Gedächtnis rufst. Benutze dazu ein Formelheft oder deine Aufzeichnungen aus dem Schulübungs- oder Merkstoffheft.
Schreibe nun den Merktext in dein Übungsheft!
1. Lies den Aufgabentext aufmerksam durch
2. Unterstreiche, wenn nötig, wichtige Informationen
3. Überlege dir welche Formeln du brauchst
4. Führe Bezeichnungen ein und stelle die zur Aufgabe gehörige Gleichung auf
Anfänger

| Verlängert man die Seiten eines Quadrats um 4cm, so ergibt sich ein um 56cm² größerer Flächeninhalt. Berechne die Seitenlänge des Ursprungsquadrats! |
Fortgeschrittene
| In einem rechtwinkeligen Dreieck ist die Summe aus der Hypotenuse und einer Kathete 64cm, die andere Kathete ist 16cm lang. Berechne die Seiten des rechtwinkeligen Dreiecks. |
und und
|
| Ein Brückenpfeiler ist 24m lang und wird in einen Fluss gestellt. Das Stück des Pfeilers, das im Erdboden versenkt wird, ist doppelt so lang, und das Stück, das aus dem Wasser herausragt, ist fünfmal so lang wie das Stück, das sich im Wasser befindet. Wie tief ist der Fluss? | 3 () |
| Ein Wasserbehälter fasst 30 Liter Wasser. Er ist 30cm breit und 50cm lang. Jemand hat eine unbekannte Menge Wasser hinein gegossen. Der Abstand des Wasserspiegels vom Boden ist 10cm größer als von der Oberkante. Wie viel Liter Wasser enthält der Behälter? | 22,5 () |
| In einem Dreieck ist die Seite c=5cm, die Höhe h=8cm lang. Um wie viele cm muss man die Seite c verlängern, wenn man die Höhe um 2cm verkürzt, damit der Flächeninhalt um 4 cm² größer wird? | 3 () |
Experten
| In einem Rechteck ist eine Seite um 5cm kürzer als die andere. Verkürzt man die längere Seite um 2cm und verlängert man die kürzere Seite um 4cm, |
und
|
| Ein Schilfrohr wächst 2m vom Ufer eines Teichs entfernt. Seine Spitze ragt 1m über die Wasseroberfläche. Zieht man es ans Ufer, so berührt die Spitze gerade den Teichrand. Wie tief ist der Teich an der Stelle wo das Schilf wächst? |
Der Teich ist 1,5m tief
|

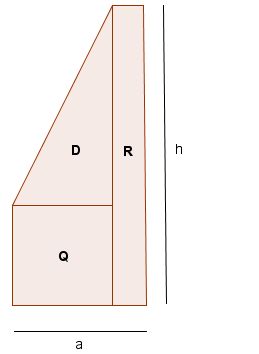
| Die drei Flächen D = Dreieck, Q = Quadrat und R = Rechteck sind gleich groß. Die Grundseite a der Figur misst 30 cm. Berechne die Höhe h. |
Die Höhe beträgt 67,5cm.
|
zurück zur Kapitelübersicht
weiter zu Kapitel 5: Verteilungsaufgaben