Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als lokale Änderungsrate

Info

In diesem Abschnitt werden Sie sich die Ableitung als momentane Änderungsrate selbst erarbeiten. Für die Bearbeitung benötigen Sie mit den Begriffen mittlere Änderungsrate und Differenzenquotient vertraut sein. Falls Ihnen die Hilfestellungen zu den Aufgaben nicht genügen steht Ihnen auf der Seite Vorwissen eine ausführlichere Zusammenfassung der benötigten Begriffe zur Verfügung.

Bild von Tacho einfügen

Der Porsche 918 Spyder

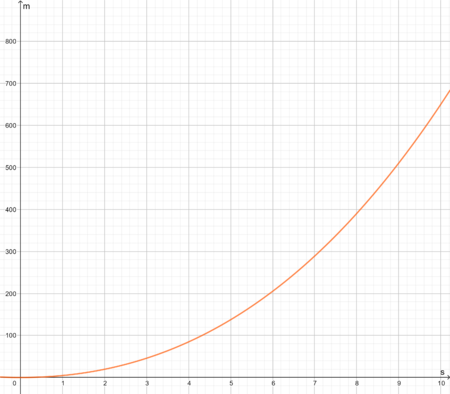
Die folgende Tabelle zeigt den Beschleunigungsvorgang des Rennautos Porsche 918 Spyder. Die Weg - Zeit - Kurve lässt sich in diesem Intervall annähernd durch die Funktion $s(t)=0,2t^2+4,5t^3$ beschreiben.

$s(t)=0,2t^2+4,5t^3$

Zeit (Sekunden)	Strecke (Meter)
0	0
1	4,7
2	19,6
3	45,9
4	84,8
5	137,5
6	205,2
7	289,1
8	390,4
9	510,3

Mittlere Änderungsrate

Aufgabe 1

Überlegen Sie zunächst welcher physikalischen Größe die mittleren Änderungsraten in diesem Zusammenhang zuzuordnen ist und wie man diese berechnet. Notieren Sie Ihre Lösung in ihrem Heft.

Die mittlere Änderungsrate gibt in diesem Zusammenhang die durchschnittliche Änderung des Weges pro Zeiteinheit an.

Die mittlere Änderungsrate gibt in diesem Zusammenhang die Durchschnittsgeschwindigkeit an und kann mit Hilfe des Differenzenquotienten berechnet werden.

Aufgabe 2

Bestimmen Sie mit welcher Durchschnittsgeschwindigkeit der Porsche in den folgenden Zeitintervallen gefahren ist.

a) zwischen Sekunde 1 und 2
b) zwischen Sekunde 2 und 3
c) zwischen Sekunde 3 und 4
Überprüfe deine Ergebnisse in folgendem Applet mit Hilfe des geometrischen Zusammenhangs der mittleren Änderungsrate und der Sekantensteigung.

zum Applet

Momentane Änderungsrate

Aufgabe 3

Bestimmen Sie nun näherungsweise wie schnell der Porsche nach 3 Sekunden gefahren ist. Wählen Sie hierzu ein beliebiges Zeitintervall in dem die dritte Sekunde enthalten ist und verkleinern Sie dieses.
a) Verkleinern Sie das Intervall in folgender Tabelle mindestens 5 mal und halten Sie die Tabelle schriftlich fest.
zur Tabelle

b) Führe die Verkleinerung des Zeitintervalls nun erneut in diesem Applet durch.
Beschreibe die Veränderung der Sekante und des Werts der Sekante bei dieser Verkleinerung und halte dies schriftlich fest.
c) Was sind die Eigenschaften dieser neu entstandenen Geraden?

Durch die beliebig gute Näherung von T1 und T2 zur Sekunde 3, lässt sich die neu entstandene Gerade als Gerade interpretieren, die nur noch den Berührpunkt $P(3|f(3))$ am Graphen von $f$ hat. Diese Gerade nennt man Tangente.

Tangente

Die Gerade, die den Graphen von $f$ am Punkt $P(x_0|f(x_0))$ berührt und die gleiche Steigung wie der Graph von $f$ in diesem Punkt hat, nennt man die Tangente von $f$ am Punkt $P$.

d) Als was lässt sich in diesem Kontext die Steigung dieser Geraden interpretieren?

Die Steigung dieser Geraden lässt sich nun als die momentane Geschwindigkeit (momentane Änderungsrate) interpretieren.

Der Differentialquotient

Aufgabe 4

a) Schauen Sie sich die Aufgaben zur Intervallverkleinerungen aus Aufgabe 2 erneut an. Notieren Sie wie man die Verkleinerung des Intervalls im Differenzenquotienten ausdrücken könnte. Das Ergebnis des neuen Quotienten soll die momentane Änderungsrate und die Steigung der Tangente darstellen.

Differentialquotient

Der Differenzenquotient $\frac{f(x_1)-f(x_0)}{x_1-x_0}$ kommt der Steigung im Punkt $P (x_0,f(x_0))$ beliebig nahe, je näher $h$ der Null kommt.

Dieser Grenzwert des Differenzenquotienten ist der Differentialquotient $f'(x_0) = \lim_{x_1\to x_0} \frac{f(x_1)-f(x_0)}{x_1-x_0}$.
Der Differentialquotient $f'(x_0)$ wird auch als Ableitung der Funktion $f$ an der Stelle $x_0$ bezeichnet.