Zentrische Streckung/Abbildung durch zentrische Streckung/4.Station: Unterschied zwischen den Versionen
K (Kilian Schoeller verschob die Seite Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/4.Station nach Zentrische Streckung/Abbildung durch zentrische Streckung/4.Station) |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken | |||
|{{Abbildungen durch zentrische Streckung}} | |||
|Lernschritte einblenden | |||
|Lernschritte ausblenden | |||
}} | |||
==4. Station: Zusammenfassung== | ==4. Station: Zusammenfassung== | ||
| Zeile 20: | Zeile 22: | ||
</div> | </div> | ||
<br> | <br> | ||
{{Fortsetzung|weiter=Übung|weiterlink=5.Station}} | |||
Version vom 22. Mai 2019, 16:02 Uhr
4. Station: Zusammenfassung
Hier siehst du alles, was du bisher herausgefunden hast zusammengefasst.
Schreibe dir diese Zusammenfassung in dein Heft!
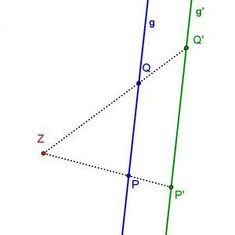
Abbildungsvorschrift der zentrischen Streckung
Wenn eine Vergrößerung von einem Zentrum ausgeht, spricht man von einer zentrischen Streckung.
Sie wird festgelegt durch Angabe eines Streckungszentrums Z und eines Streckungsfaktors k. (Kurz: ![]() )
)
Der Urpunkt P, der Bildpunkt P' und das Streckungszentrum Z liegen auf einer Geraden.
Es gilt: ZP' = |k| ∙ ZP
Bei |k|>1 liegt eine Vergrößerung, bei 0<|k|<1 eine Verkleinerung vor.
Wenn k=1 ist liegt die Identität vor, bei k= -1 eine Spiegelung.
Für k>0 gilt: Urpunkt und Bildpunkt liegen auf der gleichen Seite von Z.
Für k<0 gilt: Urpunkt und Bildpunkt liegen auf verschiedenen Seiten von Z.