Beschreibende Statistik/Qualitative und Quantitative Merkmale, Skalen: Unterschied zwischen den Versionen
main>Karl Kirst Keine Bearbeitungszusammenfassung |
main>Karl Kirst (Navigation/Lernpfad) |
||
| Zeile 1: | Zeile 1: | ||
{{Lernpfad | {{Navigation/Lernpfad| | ||
<u>'''Lernziele:'''</u> | <u>'''Lernziele:'''</u> | ||
* Sie kennen die Definitionen (und mathematischen Bezeichnungen) der Begriffe | * Sie kennen die Definitionen (und mathematischen Bezeichnungen) der Begriffe | ||
Version vom 23. Januar 2018, 18:45 Uhr
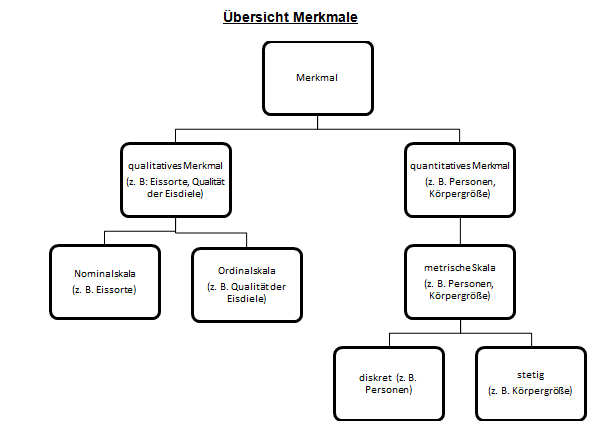
Um die statistische Erhebung auswerten zu können, müssen Merkmale mit ihren Merkmalsausprägungen weiter unterschieden werden.Man unterscheidet zwischen
- qualitativen und
- quantitativen Merkmalen.
- Quantitative Merkmale
Bei quantitativen Merkmalen lassen sich die Merkmalsausprägungen durch
- Zahlen oder
- Größenwerte
ausdrücken und in einer metrischen Skala anordnen. Mit quantitativen Merkmalen sollten einfache Rechenoperationen sinnvoll möglich sein.
Eine metrische Skala wird noch nach Art der vorkommenden Zahlen oder Größenwerte unterscheiden. Man nennt eine metrische Skala metrisch diskret, wenn nur ganze Zahlen (z. B. Personen) als Merkmalsausprägungen zugelassen sind. Können auch Dezimalzahlen als Merkmalsausprägung vorkommen, so nennt man die Skala metrisch stetig (alle Zahlen, z. B. Temperatur, Gewicht).
- Qualitative Merkmale
Qualitative Merkmale sind entweder Texte oder Zahlwerte, mit denen man aber keine sinnvollen Rechnungen ausführen kann.
Sie werden noch einmal unterschieden in solche, bei denen die Merkmalsausprägungen in eine natürliche Reihenfolge (ordinale Skala) gebracht werden können, und in jene, bei denen die Merkmalsausprägungen nicht abgestuft werden können (nominale Skala).
Beispiele:
|
Man unterscheidet in
- quantitative Merkmale, deren Merkmalsausprägungen aus Zahlen oder Größenwerten bestehen
- mit metrisch diskreter Skala (nur ganze Zahlen)
- mit metrisch stetiger Skala (alle Kommazahlen)
- qualitative Merkmale, deren Merkmalausprägungen in Textform oder als Zahlwerte (ohne mögliche sinnvolle Rechenoperationen) gegeben sind
- mit Ordinalskala (die Merkmalsausprägungen lassen sich in eine natürliche Reihenfolge bringen)
- mit Nominalskala (die Merkmalsausprägungen haben keine Wertigkeit)
|
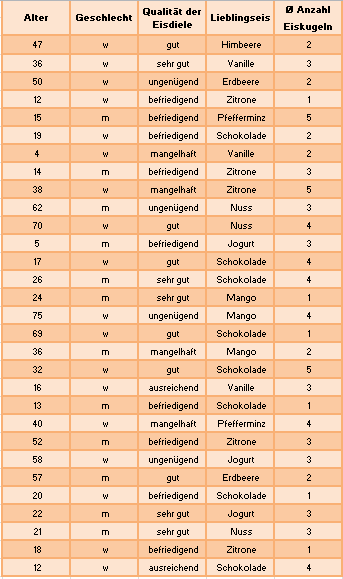
Einführungsbeispiel - Teil 4 Jetzt werden die Merkmale "Alter", "Geschlecht", "Lieblingseissorte" und "Durchschnittliche Anzahl an Eiskugeln" im Hinblick auf ihre Art und die zugehörige Skala untersucht: | |||
| Merkmal | Merkmalsausprägungen | Art des Merkmals | Skala |
|---|---|---|---|
| Alter | 0; 1; 2;...;100 | quantitativ | metrisch diskrete Skala |
| Geschlecht | m, w | qualitativ | Nominalskala |
| Qualität der Eisdiele | sehr gut, gut, befriedigend, ausreichend, mangelhaft, ungenügend | qualitativ | Ordinalskala |
| Lieblingseis | Himbeere, Vanille, Erdbeere, Pfefferminz, Schokolade, Zitrone, Mango, Jogurt, Nuss | qualitativ | Nominalskala |
| Durchschnittliche Anzahl der gegessenen Eiskugeln | 1, 2, 3, 4, 5 | quantitativ | metrisch diskrete Skala |
|
Betrachtet man das Merkmal "Geschlecht" so lauten die ersten Beobachtungswerte
Es gibt Beobachtungswerte , aber nur zwei verschiedene Merkmalsausprägungen . Jetzt legt man (beliebig) fest:
| |||