Potenzfunktionen - Einführung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Hans-Georg Weigand |
Main>Jan Wörler (→Die Graphen und ein Wanderer: - Nachfrage: Bild?) |
||
| Zeile 21: | Zeile 21: | ||
# Ein Wanderer legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W<sub>1</sub>, W<sub>2</sub>, W<sub>3</sub>. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.}} | # Ein Wanderer legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W<sub>1</sub>, W<sub>2</sub>, W<sub>3</sub>. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.}} | ||
<span style="color: RED">XXX Nachfrage: GIBTS HIER NOCH EIN BILD DAZU? (JW) XXX</span> | |||
===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2=== | ===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2=== | ||
Version vom 2. Februar 2009, 10:34 Uhr
Einführung
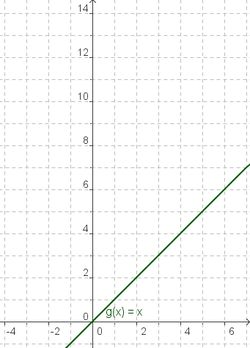
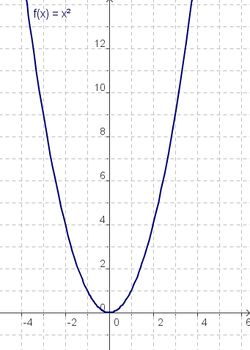
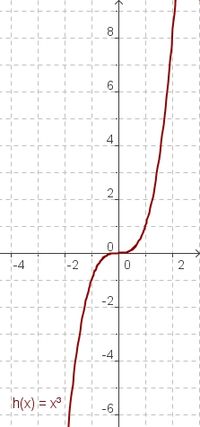
Die Graphen der Funktionen x, x² und x³
 |
 |
|
| g(x) = x | f(x) = x² | h(x) = x³ |
Die Graphen und ein Wanderer
XXX Nachfrage: GIBTS HIER NOCH EIN BILD DAZU? (JW) XXX
Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2
 |
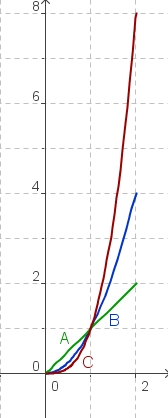g(x) = x (Graph A) f(x) = x2 (Graph B) | |||||||||||||||||||||||||||
| Vorlage:Arbeiten | ||||||||||||||||||||||||||||
|
Verändern von Variablen
Der Graph der Funktion ha(x)
| Die Datei [INVALID] wurde nicht gefunden. | Vorlage:Arbeiten |
Der Graph der Funktion ha,c(x)
| Die Datei [INVALID] wurde nicht gefunden. | Vorlage:Arbeiten |
Teste Dein Wissen
Ordne die Funktionsterme den Funktionsgraphen zu!
Noch mehr Funktionsterme zum Zuordnen!
Wähle den zum Graphen passenden Funktionsterm aus!
