Achsensymmetrische Vierecke und Dreiecke

Lernpfad

Achsensymmetrische Vierecke und Dreiecke

Achsensymmetrische Vierecke und Dreiecke

Zeitbedarf: 45 Min.
Du benötigst: dein Heft, einen Bleistift und ein Lineal!

In diesem Lernpfad sollen achsensymmtrische Vierecke und Dreicke kennengelernt werden. Dazu wollen wir als erstes nochmal wiederholen, was sich hinter dem Begriff der Achsensymmtrie verbirgt. Notiere dir Merksätze und Definitionen in dein Heft!

1.Station: Wiederholung zur Achsensymmetrie

Kannst du dich noch an den Begriff der Achsensymmetrie erinnern? Oder wann eine Figur achsensymmetrisch ist? Nein? Dann wollen wir uns diese Begriffe zusammen erarbeiten. Vielleicht fällt dir ja dann wieder ein, was es damit auf sich hat. Also los geht´s!

1.Aufgabe
In unserem alltäglichen Leben gibt es einige Gegenstände, die besondere Eigenschaften aufweisen.Hier siehst du einige Beispiele dafür. Erkennst du die Besonderheiten?
Datei:Schmetterling.gif
Hier findest du die Lösung! Vorlage:Versteckt
Fallen dir noch mehr Gegenstände aus dem Alltag ein, die symmetrisch sind? Schreibe sie dir in dein Heft auf!

Merke

Was heißt achsensymmtrisch und kongruent?:

• Eine Figur heißt achsensymmetrisch, falls man sie in zwei Teile zerlegen kann und diese sich exakt überdecken.
  
• Die beiden Hälften sind dann kongruent zueinander.
• Die Gerade durch die die Figur geteilt wird, heißt Symmetrieachse.
• Die Symmetrieachse kann dabei waagrecht, senkrecht oder quer durch die Figur verlaufen.
• Es kann auch mehr als eine Symmetriachse geben!

2.Aufgabe

Zuordnung
Ordne die Bilder den richtigen Eigenschaften zu. Dazu musst du die Flaggen mit der linken Maustaste ziehen und fallen lassen, wenn der Hintergrund rot wird.
Übertrage anschließend je zwei Flaggen mit einer und zwei Symmetrieachsen in dein Heft und zeichne die Symmetriachsen ein!

zwei Symmetrieachsen

eine Symmetrieachse

keine Symmetrieachse

mehrere Symmetrieachsen

neu starten

Konntest du alle Flaggen richtig zuordnen? Prima! Dann können wir ja zur nächsten Aufgabe gehen.

3.Aufgabe
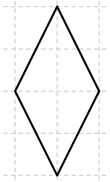
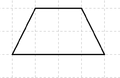
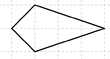
Übertrage die drei Figuren in dein Heft und erweitere sie zu einer achsensymmtrischen Figur!
Datei:Stern.png

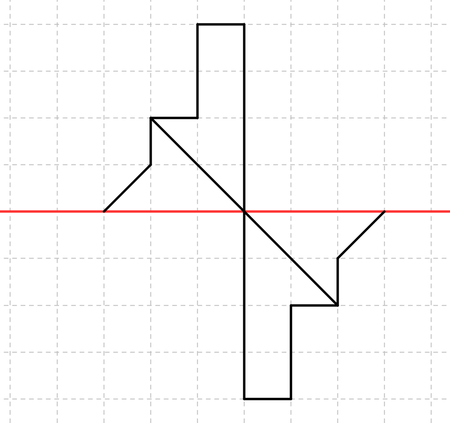
Ich denk du weißt jetzt wieder, was der Begriff der Achsensymmetrie heißt und was achsensymmetrische Figuren sind!

Bevor wir mit einem neuen Thema anfangen, lernen wir noch eine 2.Definition für das Wort achsensymmetrisch kennen. Diese hängt mit der Achsenspiegelung zusammen, die wir in den beiden vorherigen Lernpfaden durchgenommen haben.

Definition
Eine Figur, die man durch eine Achsenspiegelung auf sich selbst abbilden kann, heißt achsensymmetrisch.

2.Station:Achsensymmetrische Vierecke

4.Aufgabe
In dieser Aufgabe musst du herausfinden, welche Vierecke achsensymmetrisch sind. Es befinden sich 5 Vierecke im Such-Rätsel. Wenn du dich an Aufgabe 2 erinnerst, fallen dir vielleicht schon 2 Vierecke ein, die du bereits kennst. Viel Spass beim suchen!

Finde die Wörter! (Waagrecht (von links nach rechts), senkrecht (von oben nach unten) und schräg (von links unten nach rechts oben oder von oben links nach unten rechts), gefundene Wörter werden grün markiert)

H	X	R	P	B	P	P	H	G	M	X
S	C	F	A	Q	E	H	B	L	C	P
M	F	D	U	U	T	L	N	Y	E	Q
Q	V	A	R	N	T	R	A	P	E	Z
C	I	V	I	A	B	E	S	X	Q	W
V	Y	V	N	Q	C	C	C	S	P	E
I	N	A	S	P	I	H	B	W	C	N
Q	U	A	D	R	A	T	E	G	G	N
J	D	H	T	G	N	E	K	N	N	N
F	Q	B	A	Q	N	C	U	U	X	Y
Y	H	S	Z	M	L	K	T	X	Y	E

Erkannte Wörter

neu starten

Hast du alle Vierecke gefunden? Falls du nicht auf alle gekommen bist, findest du hier die Lösung. Vorlage:Versteckt

5.Aufgabe
In dieser Aufgabe wollen wir herausfinden, wieviel Symmetrieachsen jedes der Vierecke hat.
Ordne den Vierecken ihren Namen,ihre Symmetrieachsen und die Anzahl ihrer Symmetrieachsen zu. Dazu musst du die Bilder mit der linken Maustaste ziehen und fallenlassen, wenn der Hintergrund rot wird. Viel Spaß!

Zuordnung

1 SymmetrieachseDrachenTrapezRechteckQuadrat2 Symmetrieachsen1 Symmetrieachse2 Symmetrieachsen4 SymmetrieachsenRaute

neu starten

Überprüfe, ob du alle Symmetrieachsen gefunden hast. Vorlage:Versteckt

Merke

Achsensymmetrische Vierecke:

Man kann die Vierecke durch die Lage ihrer Symmetrieachsen unterscheiden. Dabei gibt es zwei Fälle.

• 1. Fall: Die Symmetrieachse verläuft durch die gegenüberliegenden Eckpunkte des Vierecks (Drachen, Raute).
• 2. Fall: Die Symmetrieachse geht durch die Mittelpunkte gegenüberliegender, paralleler Seiten eines Vierecks (Rechteck, Trapez).
• Beim Quadrat trifft sowohl Fall 1, als auch Fall 2 zu.

6.Aufgabe
Du kennst jetzt alle achsensymmetrsichen Vierecke und weißt, wieviel Symmetrieachsen sie haben. Kannst du auch folgende Fragen dazu richtig beantworten? Dabei können auch mehrere Antwortmöglichkeiten richtig sein.

Bei welchem Viereck verlaufen die Symmetrieachsen durch die Seitenmitten?

1. Rechteck
2. Raute
3. Quadrat
4. Raute

Welches Viereck hat vier gleich lange Seiten?

1. Rechteck
2. Quadrat
3. Drachen
4. Raute

Welche Vierecke haben mehr als eine Symmetrieachse?

1. Quadrat
2. Rechteck
3. Trapez
4. Drachen
5. Raute

Die Raute hat ...?

1. je zwei Paar gleich großer Winkel
2. rechte Winkel
3. ein Paar gleich großer Winkel

Bei welchem Viereck stehen die Symmetrieachsen senkrecht aufeinander?

1. Raute
2. Trapez
3. Rechteck

prüfen!

neu starten

Hat du alle Fragen richtig beantwortet? Dann geht´s jetzt zur nächsten Station.

3.Station:Achsensymmetrische Dreiecke

$\Leftarrow$ Zurück