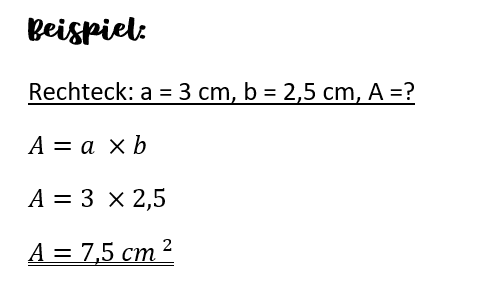Benutzer:Madlen.hochstaffl/Rechteck und Quadrat

In Bearbeitung https://unterrichten.zum.de/wiki/Fl%C3%A4cheninhalt_des_Rechtecks

Lernpfad

Zielsetzung: Schüler*innen lernen Schritt für Schritt die Eigenschaften von Rechteck und Quadrat kennen und setzen sich mit der Flächen- und Umfangberechnung auseinander.

Altersstufe: 5. Klasse MS

Zeitbedarf: ca. 8 Unterrichtsstunden

Materialien: Laptop, Geometrieheft, Schreibzeug, Geodreieck, gespitzter Bleistift, Zirkel

😎🙌👩‍💻👨‍💻✍️

Aktivierung des Vorwissens und Eigenschaften von Rechteck und Quadrat

Aktivierung des Vorwissens

Die folgenden Aufgaben können auch mehrere richtige Antworten enthalten!

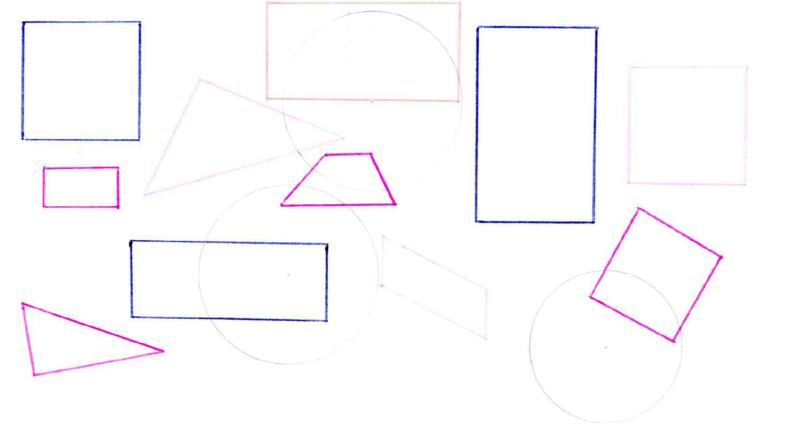
Kreuze an!

Wie viele Rechtecke erkennst du im Bild? (4) (!5) (!3)

Wie viele Quadrate erkennst du im Bild? (!4) (3) (!5)

Welche anderen geometrischen Figuren sind im Bild zu sehen? (Dreieck) (!Würfel) (Parallelogramm) (Trapez) (!Kugel) (Kreis)

Merke

Eigenschaften eines Rechtecks

• 4 rechte Winkel
• Benachbarte Seiten stehen normal aufeinander
• Gegenüberliegende Seiten sind parallel und gleich lang
• Die Diagonalen sind gleich lang und halbieren einander
• Das Rechteck ist ein besonderes Viereck

Schreiben

1. Schreibe die Überschrift RECHTECK UND QUADRAT auf einer neuen Seite in dein Geometrieheft.
2. Hole dir bei der Lehrperson das Bild des Rechtecks.
3. Schreibe als Unterüberschrift Eigenschaften eines Rechtecks, klebe das Bild vom Rechteck ein und schreibe den Merktext ins Heft ab.
4. Zeige deine Heftseite der Lehrperson.

Üben

Kreuze an. Verwende dazu den Merktext und das Bild des Rechtecks.

Die beiden Diagonalen in einem Rechteck schließen immer einen rechten Winkel ein. (!wahr) (falsch)

In einem Rechteck sind jeweils zwei Seiten gleich lang? (wahr) (!falsch)

AB || BD (!wahr) (falsch)

CD || AB (wahr) (!falsch)

AC ⊥ BD (falsch) (!wahr)

AB ⊥ BC (!falsch) (wahr)

Merke

Eigenschaften eines Quadrats

• 4 rechte Winkel
• 4 gleich lange Seiten
• Benachbarte Seiten stehen normal aufeinander
• Gegenüberliegende Seiten sind parallel und gleich lang
• Die Diagonalen sind gleich lang und halbieren einander
• Die Diagonalen stehen normal aufeinander
• Das Quadrat ist ein besonderes Rechteck

Schreiben

1. Hole dir bei der Lehrperson das Bild des Quadrats.
2. Schreibe als Unterüberschrift Eigenschaften eines Quadrats, klebe das Bild vom Quadrat ein und schreibe den Merktext ins Geometrieheft ab.
3. Zeige deine Heftseite der Lehrperson.

Üben

Setze die richten Wörter ein. Verwende dazu den Merktext und das Bild des Quadrats.

Alle vier Seiten() sind bei einem Quadrat gleich lang. Die Diagonalen des Quadrats schließen einen rechten() Winkel ein und halbieren() einander. Die Strecke AB ist parallel() zur CD.

Konstruktionen von Rechteck und Quadrat

Rechteck - Konstruktion

Sieh dir die Schritte an, die du benötigst, um ein Rechteck zu konstruieren:

Rechteck: a = 3 cm, b = 2 cm

• Zeichne die Strecke AB mit der Länge 3 cm.
• Zeichne in den Punkten A und B zwei Normalen ein.
• Schlage auf diesen Normalen mit dem Zirkel die Strecke b mit der Länge 2 cm ab. Du erhälst die Punkte C und D.
• Verbinde die Punkte C und D.
• Beschrifte das Rechteck vollständig.

Jetzt bist du an der Reihe!

Zeichne folgende Rechtecke in dein Geometrieheft:

• a = 4 cm , b = 3 cm
• a = 4 cm 7 mm , b = 5,5 cm

Wenn du fertig bist, zeige deiner Lehrperson die beiden konstruierten Rechtecke!

Quadrat - Konstruktion

Die Konstruktion eines Quadrates funktioniert genau gleich wie die eines Rechtecks. Einziger Unterschied: Alle vier Seiten sind gleich lang.

Jetzt bist du an der Reihe!

Zeichne folgende Quadrate in dein Geometrieheft und gib die Länge der Diagonalen an:

• a = 5 cm ,
  d = 7 () cm

• a = 35 mm ,
  d = 5 () cm

Wenn du fertig bist, zeige deiner Lehrperson die beiden konstruierten Quadrate!

Expertenaufgabe

Konstruiere ein Quadrat mit der Diagonale d = 6 cm. Diskutiere mit einem Mitschüler bzw. einer Mitschülerin, wie man hierbei vorgehen könnte. Wenn du fertig bist, zeige deiner Lehrperson deine Idee!

Umfang von Rechteck und Quadrat

Experimentieren

Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn bzw. deiner Nachbarin, wie du den Umfang eines Rechtecks berechnen kannst. https://www.geogebra.org/m/MhZVUNpe#material/q2fuqXUV

Was ist ein Umfang?

Erkläre danach einem Schulkollegen bzw. einer Schulkollegin, was ein Umfang einer Figur ist. Haltet eure Ergebnisse hier fest: https://www.menti.com/aly62opm9o2c

Merke

Schreibe den folgenden Merksatz ins Geometrieheft (Überschrift: Umfang eines Rechtecks)

Den Umfang eines Rechtecks kannst du mit folgenden Formeln berechnen:

• $u = a + b + a + b$
• $u = 2 \times a + 2 \times b$
• $u = 2 \times (a + b)$

Welche Formel du zur Berechnung verwendet, ist dir selbst überlassen.

Jetzt bist du an der Reihe!

Jetzt bist du an der Reihe

Berechne den Umfang eines Rechtecks mit folgenden Angaben: a = 51 mm, b = 3 cm. Achte auf die Einheiten. Orientiere dich am Beispiel oben.

Experimentieren

Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn, wie du den Umfang eines Quadrats berechnen kannst. https://www.geogebra.org/m/Bh9Xb7KT

Merke

Schreibe den folgenden Merksatz ins Geometrieheft (Überschrift: Umfang eines Quadrats)

Den Umfang eines Quadrats kannst du mit folgenden Formeln berechnen. Welche Formel du zur Berechnung verwendet, ist dir selbst überlassen.

• $u = a + a + a + a$
• $u = 4\times a$

Üben: Kreuzworträtsel

Üben

sechszig	Quadrat: a = 15, u = ?
sechsundzwanzig	Rechteck: a = 6 , b = 7 , u = ?
hundertsechsundneunzig	Quadrat: a = 49 , u = ?
zehntausendeinundsechzig	Rechteck : a = 968 , b = ? , u = 22 058
vier	Quadrat: u = 16 , a = ?
zweihundertsechsundfünzig	Rechteck: a = 70 , b = 58 , u = ??

Flächenberechnung von Rechteck und Quadrat

Flächenmaße

Der Umfang ist eine Länge und wird mit Längenmaßen angegeben z.B. cm, dm, mm, .... Nun aber wird es um den Flächeninhalt gehen. In welcher Einheit eine Fläche angegeben wird, erfährst du beim Bearbeiten der nachfolgenden Aufgaben.

Geogebra Flächeninhalt

Sieh dir die Geogebra Datei an und experimentiere. Besprich mit einem Schulkollegen bzw. einer Schulkollegin, wie man die Fläche eines Rechtecks berechnen kann. https://www.geogebra.org/m/FexywbYW

Video

Sieh dir das Video zur Berechnung des Flächeninhalts eines Rechtecks an:

https://studyflix.de/mathematik/flaecheninhalt-rechteck-2550

Merke

Scheibe den folgenden Merktext ins Geometrieheft. Überschrift: Flächeninhalt Rechteck und Quadrat.

Jede Figur hat einen Flächeninhalt (A). Das ist die Anzahl der Flächeneinheiten, die in der Fläche enthalten sind. Die Fläche eines Rechtecks wird berechnet mit der Formel:

$A = a \times b$

Video

Sieh dir das Video zur Berechnung des Flächeninhalts eines Quadrats an:

Video

Sieh dir das Video zur Berechnung des Flächeninhalts eines Quadrats an: https://studyflix.de/mathematik/flaecheninhalt-quadrat-2552

Merke

Schreibe im bereits angefangenen Merktext weiter:

Die Fläche eines Quadrats wird berechnet mit der Formel:

$A = a \times a$

Üben

Was musst du berechnen? Fläche oder Umfang?

Rechenaufgaben --> Was muss ich berechnen? Umfang oder Flächeninhalt? Ergebnis

Für schnelle Rechenfüchse

Schneide aus einem Blatt Papier 24 Quadrate mit 5 cm Seitenlänge. Lege damit verschiedene Rechtecke, wobei kein Quadratplättchen übrig bleiben darf. Berechne dann jeweils den Umfang und den Flächeninhalt.

Expertenaufgabe: Zusammengesetzte Figuren, Flächengleiche Rechtecke und Quadrate Nr 701 von Genial

Weitere Lernmöglichkeiten: Rechteck - Flächeninhalt und Eigenschaften