Modellieren digital/Schlosspark: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken| | |||
[[Modellieren_digital|Einleitung]] | |||
[[Modellieren_digital/Schlosspark|Aufgabe 1: Schlosspark]] | |||
[[Modellieren_digital/Tower|Aufgabe 2: Kölner Tower]] | |||
[[Modellieren_digital/Spielplatz|Aufgabe 3: Spielplatz]] | |||
[[Modellieren_digital/Torschuss|Aufgabe 4: Torschuss]] | |||
[[Modellieren_digital/Supermarkt|Aufgabe 5: Supermarkt]] | |||
[[Modellieren_digital/Volleyball|Aufgabe 6: Volleyball]] | |||
}} | |||
{{Box|Aufgabe| | {{Box|Aufgabe| | ||
[[Datei:Schloßpark Pillnitz.JPG|links|mini]] In der Abbildung links siehst du ein Foto vom Pillnitzer Schlosspark. Durch die vielen Besucherinnen und Besucher wird der Rasen stark beansprucht. Daher muss dieser regelmäßig erneuert werden. | [[Datei:Schloßpark Pillnitz.JPG|links|mini]] In der Abbildung links siehst du ein Foto vom Pillnitzer Schlosspark. Durch die vielen Besucherinnen und Besucher wird der Rasen stark beansprucht. Daher muss dieser regelmäßig erneuert werden. | ||
Version vom 17. Juli 2022, 10:41 Uhr
Bei der Aufgabe Schlosspark handelt es sich um eine Modellierungsaufgabe. Solche Aufgaben weisen besondere Eigenschaften auf. Zum Beispiel können sie unwichtige Informationen im Aufgabentext enthalten und genauso können wichtige Informationen fehlen. Überlege kurz, wie das bei der Aufgabe Schlosspark ist!
Außerdem können Modellierungsaufgaben auf verschiedene Arten gelöst werden und erfordern mehrere Teilschritte. Wie die Schritte ablaufen können und wie man mit verschiedenen Lösungen zum Ziel kommt, lernst du auf dieser Seite am Beispiel der Aufgabe Schlosspark kennen.Schritt 1: Vereinfachen
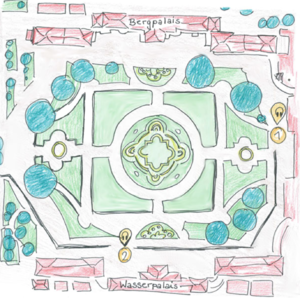
Um die Frage zu beantworten, schauen wir uns einen Ausschnitt des Parkplans an (siehe Abbildung rechts).
Überlege zunächst,
- welche Grünflächen überhaupt zum Schlosspark gehören,
- wie die Stellen aussehen könnten, die von Bäumen verdeckt werden
- und welche Vereinfachungen du noch treffen solltest.
Notiere das Ergebnis, indem du mindestens drei Vereinfachungen in deinem Hefter formulierst.
Schritt 2: Mathematisches Modell suchen
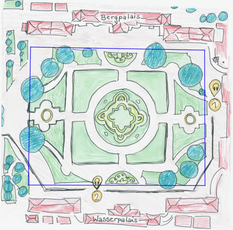
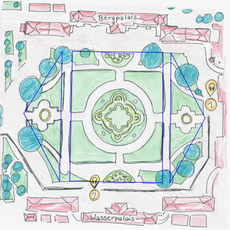
Nachdem Vereinfachungen formuliert wurden, muss man entscheiden, wie man den Flächeninhalt mit Hilfe der Mathematik berechnen kann. Hier ist dargestellt, wie zwei Schüler die Fläche unterschiedlich vereinfacht und verschiedene Formen zur Modellierung der Rasenfläche benutzt haben.
Wähle eins der beiden Modelle aus und notiere dies in deinem Hefter.
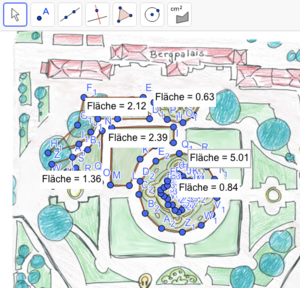
Schritt 3: Mathematisch Arbeiten
Ermittle nun mit Hilfe von GeoGebra den Flächeninhalt der eingezeichneten blauen Figur. Wähle das erste GeoGebra-Applet, wenn du dich vorhin für Modell 1 entschieden hast und das zweite GeoGebra-Applet, wenn du dich vorhin für Modell 2 entschieden hast.
Noch ein Hinweis: Eine Längeneinheit in dem GeoGebra-Applet entspricht 16,8 m in Wirklichkeit.
Modell 1:

Modell 2:

Schritt 4: Interpretieren
Formuliere in deinem Hefter einen Antwortsatz.
Schritt 5: Kontrollieren
Nach der Rechnung sollte man das Ergebnis kontrollieren. Beantworte dazu die Fragen in deinem Hefter.
Neues Modell
Versuche nun, eine bessere Modellierung für den Schlosspark zu finden.
Noch ein Hinweis: Eine Längeneinheit in dem GeoGebra-Applet entspricht 16,8 m in Wirklichkeit.

Ergebnis
Beantworte in deinem Hefter folgende Fragen:
- Wie viele Quadratmeter Rasenfläche hat der Schlosspark?
- Beschreibe dein Vorgehen in GeoGebra!
Es soll die Grünfläche einer Parkanlage berechnet werden. Dies Fläche wird als eben angenommen und der Garten ist symmetrisch. Das Muster beim Brunnen wird nicht gesondert berechnet. Die Grünflächen werden durch Vielecke angenähert, wobei die von den Symbolen verdeckten Stellen ähnlich den gegenüberliegenden Figuren angenähert werden.
Die Grünfläche der Parkanlage ist also etwa 8200 m2 groß.
Wenn der Rasen durch einen Rollrasen erneuert wird, so sind eventuell aber zusätzlich noch Reserven einzuplanen, da mit relativ viel Verschnitt zu rechnen ist. Werden Rasensamen gestreut, sind diese Mengen nicht auf den Quadratmeter genau zu kaufen.
Erstellt von: Lena Frenken (Diskussion)