Signifikanztest für binomialverteilte Zufallsgrößen/Fehlerarten beim Signifikanztest: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(Beispiel hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 8: | Zeile 8: | ||
|3=Merksatz}} | |3=Merksatz}} | ||
<br> | <br> | ||
'''Beispiel:''' | |||
71% der Menschen in Deutschland sehen den Klimawandel als Bedrohung an.<br> | |||
<math>H_0:p\leq0,71</math> und <math>H_1:p>0,71</math><br> | |||
<div class="lueckentext-quiz"> | |||
Ein Zufallsexperiment mit genau zwei Ergebnissen (Treffer und Niete) nennt man ''' Bernoulli-Experiment'''. Wird solch ein Experiment n-mal wiederholt, und sind die Versuche unabhängig voneinander, erhält man eine '''Bernoulli-Kette''' der Länge n. Ist p die Trefferwahrscheinlichkeit und X eine Zufallsvariable, welche die Anzahl k der Treffer angibt, dann kann die Wahrscheinlichkeit für k Treffer durch die '''Formel von Bernoulli''' (<math>P(X=k)=\tbinom{n}{k}\cdot p^k \cdot (1-p)^{n-k}</math>) berechnet werden. Die Wahrscheinlichkeitsverteilung für X heißt '''Binomialverteilung''' mit den Parametern n und p. Neben der Binomialverteilung benötigt man auch häufig die zugehörige '''Verteilungsfunktion''', für deren Wahrscheinlichkeit die Schreibweise <math>P(X\leq k)</math> üblich ist. Die kumulierten Wahrscheinlichkeiten werden wie folgt berechnet: <math>P(X\leq k)=\sum_{i=0}^k B_{n,p}(i)</math> | |||
</div>|3=Arbeitsmethode | |||
[[Datei:Example.png|700px]] | [[Datei:Example.png|700px]] | ||
Version vom 30. November 2019, 10:50 Uhr
Beim Signifikanztest können zwei Fehlentscheidungen auftreten.
Folgende Tabelle stellt beide Fehlerarten dar.
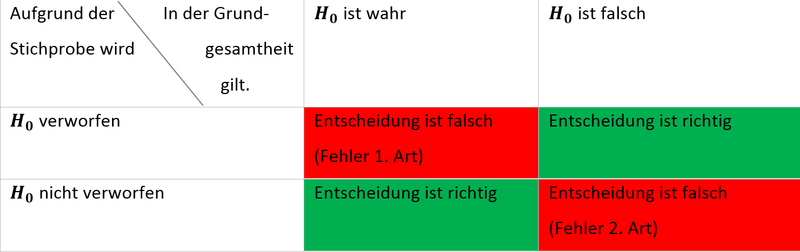
Der Fehler 1. Art wird oft auch als -Fehler bezeichnet. Diesen Fehler habt ihr bereits kennengelernt. Beim Fehler 1. Art wird eine richtige Nullhypothese fälschlicherweise verworfen. Dieser Fehler wird durch das festgelegte Signifikanzniveau kontrolliert. Die Wahrscheinlichkeit für den Fehler 1. Art kann also nie größer, als das festgelegte Signifkanzniveau sein.
Beispiel:
71% der Menschen in Deutschland sehen den Klimawandel als Bedrohung an.
und
Ein Zufallsexperiment mit genau zwei Ergebnissen (Treffer und Niete) nennt man Bernoulli-Experiment. Wird solch ein Experiment n-mal wiederholt, und sind die Versuche unabhängig voneinander, erhält man eine Bernoulli-Kette der Länge n. Ist p die Trefferwahrscheinlichkeit und X eine Zufallsvariable, welche die Anzahl k der Treffer angibt, dann kann die Wahrscheinlichkeit für k Treffer durch die Formel von Bernoulli () berechnet werden. Die Wahrscheinlichkeitsverteilung für X heißt Binomialverteilung mit den Parametern n und p. Neben der Binomialverteilung benötigt man auch häufig die zugehörige Verteilungsfunktion, für deren Wahrscheinlichkeit die Schreibweise üblich ist. Die kumulierten Wahrscheinlichkeiten werden wie folgt berechnet:
|3=Arbeitsmethode
Es gibt ein Malaria- Schnelltest. Die Nullhypothese lautet, die gesteste Person hat kein Malaria (Test ist negativ). Die Gegenhypothese lautet, die Person hat Malaria (Test ist positiv).
Beschreibe in Worten, worin der Fehler 1. Art besteht.
Beschreibe in Worten, worin der Fehler 2. Art besteht.
Im Gericht soll überprüft werden, ob ein Angeklagter schuldig ist. Im freiheitlichen Rechtsstaat gilt die Nullhypothese : Der Angeklagte ist unschudlig. Die Gegenhypothese lautet demnach, der Angeklagte ist schuldig.
Beschreibe in Worten, worin der Fehler 1. Art besteht.
Beschreibe in Worten, worin der Fehler 2. Art besteht.
Nun schauen wir uns an, wie die Fehler berechnet werden.
Für die Berechnung des Fehlers 1. Art und Fehlers 2. Art, muss die tatsächliche geltende Verteilung angegeben sein. Mit dieser Verteilung berechnest du den Fehler 1. und Fehler 2. Art aus.
Beim Fehler 1. Art berechnest du die kumulierte Wahrscheinlichkeit des Verwerfungsbereichs mit der Verteilung, die tatsächlich gilt. HINWEIS: Oft gilt eine andere Verteilung, als mit der du im Signifikanztest den Annahme- und Verwerfungsbereich ermittelt hast. Wenn tatsächlich der Grenzfall der Nullhypothese die tasächliche Verteilung ist, dann ist der Fehler 1. Art gleich dem festgelegten Signifikanzniveau. FORMEL




