Zentrische Streckung/Abbildung durch zentrische Streckung/4.Station: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 7: | Zeile 7: | ||
==4. Station: Zusammenfassung== | ==4. Station: Zusammenfassung== | ||
Hier siehst du alles, was du bisher herausgefunden hast zusammengefasst. | Hier siehst du alles, was du bisher herausgefunden hast, zusammengefasst. | ||
Schreibe dir diese Zusammenfassung in dein Heft! | |||
Schreibe dir diese Zusammenfassung in dein Heft! | |||
{{Box|1=Abbildungsvorschrift der zentrischen Streckung|2= | {{Box|1=Abbildungsvorschrift der zentrischen Streckung|2= | ||
[[Bild:Porzelt_Dia-3.jpg| | [[Bild:Porzelt_Dia-3.jpg|right]] | ||
*Wenn eine Vergrößerung von einem Zentrum ausgeht, spricht man von einer '''zentrischen Streckung'''. | *Wenn eine Vergrößerung von einem Zentrum ausgeht, spricht man von einer '''zentrischen Streckung'''. | ||
*Sie wird festgelegt durch Angabe eines '''Streckungszentrums Z''' und eines '''Streckungsfaktors k'''. (Kurz: [[Bild:Porzelt_Pfeil-1.jpg]] ) | *Sie wird festgelegt durch Angabe eines '''Streckungszentrums Z''' und eines '''Streckungsfaktors k'''. (Kurz: [[Bild:Porzelt_Pfeil-1.jpg]] ) | ||
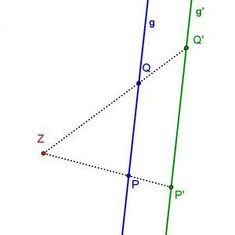
*Der '''Urpunkt P''', der '''Bildpunkt P'''' und das Streckungszentrum Z liegen auf einer Geraden. | *Der '''Urpunkt P''', der '''Bildpunkt P'''' und das Streckungszentrum Z liegen auf einer Geraden. | ||
*Es gilt: <math>\overline{ZP^{'}} = \mid k \mid \cdot \overline{ZP} </math> | *Es gilt: <math>\overline{ZP^{'}} = \mid k \mid \cdot \overline{ZP} </math> | ||
*Bei <math>\mid k \mid > 1</math> liegt eine Vergrößerung, bei <math>0 < \mid k \mid < 1</math> eine Verkleinerung vor. | *Bei <math>\mid k \mid > 1</math> liegt eine Vergrößerung, bei <math>0 < \mid k \mid < 1</math> eine Verkleinerung vor. | ||
*Wenn <math>k = 1</math> ist liegt die Identität vor, bei <math>k = -1</math> eine Spiegelung. | *Wenn <math>k = 1</math> ist liegt die Identität vor, bei <math>k = -1</math> eine Spiegelung. | ||
*Für <math>k > 0</math> gilt: Urpunkt und Bildpunkt liegen auf der gleichen Seite von Z. | *Für <math>k > 0</math> gilt: Urpunkt und Bildpunkt liegen auf der gleichen Seite von Z. | ||
*Für <math>k < 0</math> gilt: Urpunkt und Bildpunkt liegen auf verschiedenen Seiten von Z. | *Für <math>k < 0</math> gilt: Urpunkt und Bildpunkt liegen auf verschiedenen Seiten von Z. | ||
|3=Merksatz}} | |3=Merksatz}} | ||
| Zeile 24: | Zeile 33: | ||
{{Fortsetzung|weiter=Übung|weiterlink=../5.Station}} | {{Fortsetzung|weiter=Übung|weiterlink=../5.Station}} | ||
[[Kategorie:Mathematik]] | |||
[[Kategorie:ZUM2Edutags]] | |||
Version vom 17. August 2019, 07:19 Uhr
4. Station: Zusammenfassung
Hier siehst du alles, was du bisher herausgefunden hast, zusammengefasst.
Schreibe dir diese Zusammenfassung in dein Heft!
Abbildungsvorschrift der zentrischen Streckung
- Wenn eine Vergrößerung von einem Zentrum ausgeht, spricht man von einer zentrischen Streckung.
- Sie wird festgelegt durch Angabe eines Streckungszentrums Z und eines Streckungsfaktors k. (Kurz:
)
- Der Urpunkt P, der Bildpunkt P' und das Streckungszentrum Z liegen auf einer Geraden.
- Es gilt:
- Bei liegt eine Vergrößerung, bei eine Verkleinerung vor.
- Wenn ist liegt die Identität vor, bei eine Spiegelung.
- Für gilt: Urpunkt und Bildpunkt liegen auf der gleichen Seite von Z.
- Für gilt: Urpunkt und Bildpunkt liegen auf verschiedenen Seiten von Z.
