Beschreibende Statistik/Absolute und Relative Häufigkeiten: Unterschied zwischen den Versionen
main>Nina Krämer Keine Bearbeitungszusammenfassung |
main>Nina Krämer Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Lernpfad-M| | |||
<u>'''Lernziele:'''</u> | |||
* Sie kennen die Definitionen (und mathematischen Bezeichnungen) der Begriffe | |||
** arithmetisches Mittel (Mittelwert, Durchschnitt), | |||
** Modus (Modalwert) und | |||
** Median (Zentralwert). | |||
* Sie können | |||
** das arithmetische Mittel, | |||
** den Modus und | |||
** den Median | |||
::: im Sachzusammenhang berechnen, wenn die Daten als | |||
* Urliste mit Beobachtungswerten, | |||
* als absolute Häufigkeitsverteilung oder | |||
* als relative Häufigkeitsverteilung vorliegen. | |||
* Sie können | |||
** das arithmetische Mittel, | |||
** den Modus und | |||
** den Median | |||
::: interpretieren und die Aussagekraft des Lagemaßes beurteilen. | |||
Sie kennen das alles schon? Dann geht es hier direkt zu den Übungen [[Datei:Pfeil 2.gif]] [[../Übungen Absolute und Relative Häufigkeiten|Übungen]] | |||
Ansonsten sind Sie hier richtig. | |||
}} | |||
Gerade bei großem Stichprobenumfang ist die Urliste nicht aussagekräftig. Hat man nicht zu viele verschiedene Merkmalsausprägungen, kann man die Häufigkeit festzustellen, mit der ein Merkmal eine bestimmte Ausprägung annimmt. Die Häufigkeit kann in '''absoluten Zahlen''' angegeben werden oder als '''relativer Anteil''' am Umfang der Stichprobe. Denken Sie immer daran, jede Aufbereitung soll die Daten aussagekräftiger machen. Meistens sollen die Daten eine Aussage unterstützen. | Gerade bei großem Stichprobenumfang ist die Urliste nicht aussagekräftig. Hat man nicht zu viele verschiedene Merkmalsausprägungen, kann man die Häufigkeit festzustellen, mit der ein Merkmal eine bestimmte Ausprägung annimmt. Die Häufigkeit kann in '''absoluten Zahlen''' angegeben werden oder als '''relativer Anteil''' am Umfang der Stichprobe. Denken Sie immer daran, jede Aufbereitung soll die Daten aussagekräftiger machen. Meistens sollen die Daten eine Aussage unterstützen. | ||
| Zeile 126: | Zeile 151: | ||
|} | |} | ||
<!-- Ende Einführungsbeispiel Teil 5 --> | <!-- Ende Einführungsbeispiel Teil 5 --> | ||
{{Lernpfad-M| | |||
Sie haben Ihr Regelheft mit dem ersten Merksatz gefüllt. | |||
Testen Sie Ihr Wissen. [[Datei:Pfeil 2.gif]] [[../Übungen Absolute und Relative Häufigkeiten|Übungen]] | |||
[[../|zurück | [[../../Lernpfad zur Beschreibenden Statistik|zurück zur Startseite des Lernpfad]] | ||
}} | |||
Version vom 10. April 2015, 22:15 Uhr
Gerade bei großem Stichprobenumfang ist die Urliste nicht aussagekräftig. Hat man nicht zu viele verschiedene Merkmalsausprägungen, kann man die Häufigkeit festzustellen, mit der ein Merkmal eine bestimmte Ausprägung annimmt. Die Häufigkeit kann in absoluten Zahlen angegeben werden oder als relativer Anteil am Umfang der Stichprobe. Denken Sie immer daran, jede Aufbereitung soll die Daten aussagekräftiger machen. Meistens sollen die Daten eine Aussage unterstützen.
Gibt es sehr viele verschiedene Merkmalsausprägungen, so müssen die Merkmalsausprägungen zunächst zu Klassen zusammen gefasst werden. Dazu im nächsten Abschnitt mehr.
| Beispiel "Alter der Lerngruppe": | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Die Urliste zum Merkmal "Alter der Lerngruppe" hat einen Stichprobenumfang von und enthält folgende Beobachtungswerte:
Das Merkmal "Alter der Lerngruppe" hat Merkmalsausprägungen, nämlich: Jetzt lassen sich die absoluten Häufigkeiten leicht durch abzählen berechnen (ideal sind hier Strichlisten), man erhält:
| |||||||||||||||||||||
| Diese Art die Beobachtungswerte zu präsentieren nennt man absolute Häufigkeitsverteilung.
Oft interessieren die genauen Zahlen aber gar nicht, sondern es geht nur um Anteile vom Ganzen. Berechnet man aus der absoluten Häufigkeitsverteilung jetzt die relativen Anteile der Merkmalsausprägungen bezogen auf den Stichprobenumfang, so erhält man die folgende Tabelle:
| |||||||||||||||||||||
| Diese Art die Beobachtungswerte zu präsentieren nennt man relative Häufigkeitsverteilung.
Will man nicht mit Brüchen arbeiten, so hat es sich bewährt, Dezimalzahlen mit mindestens 3 Nachkommastellen darzustellen oder alternativ Prozentzahlen mit einer Dezimale. Aber oft sind die Darstellung als Bruch zu bevorzugen, weil es dann keine Rundungsdifferenzen gibt. |
Die absolute Häufigkeit gibt die Anzahl aller Merkmalsträger mit dieser Merkmalsausprägung an.
Statt schreibt man auch kurz .
Die relative Häufigkeit gibt den Anteil aller Merkmalsträger mit dieser Merkmalsausprägung bezogen auf den Stichprobenumfang an.
Statt schreibt man auch kurz .
Die Summe der absoluten Häufigkeiten ist immer gleich der Anzahl aller Merkmalsträger, also gleich dem Stichprobenumfang.
Mathematische Kurzschreibweise:
- oder noch kürzer ,
wobei die Anzahl der Merkmalsausprägungen und den Stichprobenumfang bezeichnen.
Eine Darstellung der Merkmalsausprägungen mit absoluten Häufigkeiten nennt man absolute Häufigkeitsverteilung.
Die Summe der relativen Häufigkeiten ist immer gleich 1, also 100 %.
Mathematische Kurzschreibweise:
- oder noch kürzer ,
wobei die Anzahl der Merkmalsausprägungen und den Stichprobenumfang bezeichnen.
Eine Darstellung der Merkmalsausprägungen mit relativen Häufigkeiten nennt man relative Häufigkeitsverteilung.
|
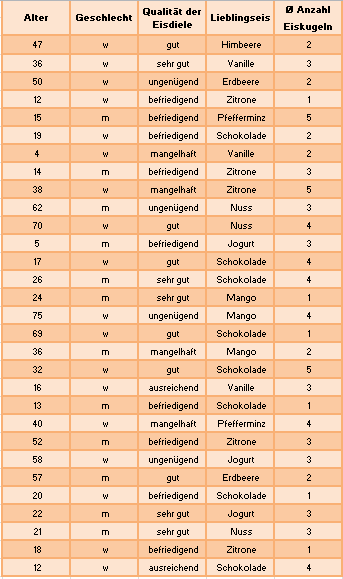
Einführungsbeispiel - Teil 5 Jetzt kann mit dem nächsten Schritt der Aufbereitung der Umfrage der Eisdiele "Rabe" begonnen werden. Hier soll das Merkmal "Geschlecht" mit absoluten und später mit relativen Häufigkeiten dargestellt werden. Festgelegt wurde schon für männlich und für weiblich
| |||||||||||
|
Betrachtet man nun die relative Häufigkeit, so erhält man diese indem jede absolute Häufigkeit durch den Stichprobenumfang dividiert wird:
| |||||||||||