Achsensymmetrische Vierecke und Dreiecke: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
K (Kilian Schoeller verschob die Seite Achsenspiegelung/Achsensymmetrische Vierecke und Dreiecke nach Achsensymmetrische Vierecke und Dreiecke, ohne dabei eine Weiterleitung anzulegen) |
Version vom 12. November 2018, 14:30 Uhr
Notiere alle Merksätze und Definitionen in dein Heft!
- Zeitbedarf
- 45 Min.
- Material
- dein Heft, Stifte und ein Lineal!
1.Station: Wiederholung zur Achsensymmetrie
Kannst du dich noch an den Begriff der Achsensymmetrie erinnern? Oder wann eine Figur achsensymmetrisch ist? Nein? Dann wollen wir uns diese Begriffe zusammen erarbeiten. Vielleicht fällt dir ja dann wieder ein, was es damit auf sich hat. Also los geht´s!
In unserem alltäglichen Leben gibt es einige Gegenstände, die besondere Eigenschaften aufweisen.Hier siehst du einige Beispiele dafür. Erkennst du die Besonderheiten?
Hier findest du die Lösung!
Du siehst, dass alle Figuren in der Mitte geteilt werden können. Beide Teile haben dieselben Merkmale. Sie werden daher symmetrisch genannt. Wenn man die beiden Teile übereinander legt, überdecken sie sich, d.h sie sind dann deckungsgleich oder kongruent. Da diese Gegenstände aus der Natur kommen, sind sie natürlich nicht zu 100% kongruent. Die Gerade in der Mitte nennen wir Symmetrieachse.
- Eine Figur heißt achsensymmetrisch, falls man sie in zwei Teile zerlegen kann und diese sich exakt überdecken.
- Die beiden Hälften sind dann kongruent zueinander.
- Die Gerade durch die die Figur geteilt wird, heißt Symmetrieachse.
- Die Symmetrieachse kann dabei waagrecht, senkrecht oder diagonal durch die Figur verlaufen.
- Es kann auch mehr als eine Symmetriachse geben!
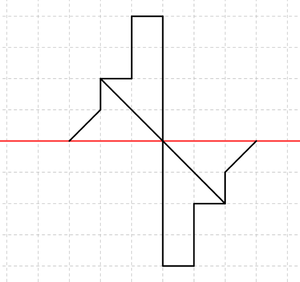
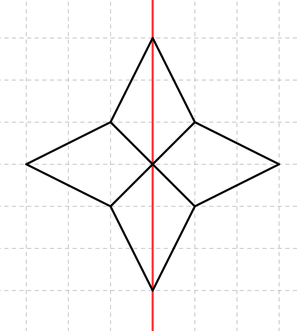
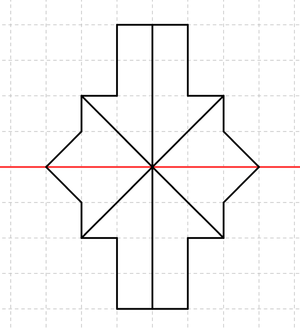
Übertrage die drei Figuren in dein Heft und erweitere sie zu einer achsensymmetrischen Figur!
Hier findest du die Lösung!Ich denke, du weißt jetzt wieder, was der Begriff der Achsensymmetrie heißt und was achsensymmetrische Figuren sind!
Bevor wir mit einem neuen Thema anfangen, lernen wir noch eine 2.Definition für das Wort achsensymmetrisch kennen. Diese hängt mit der Achsenspiegelung zusammen, die wir in den beiden vorherigen Lernpfaden durchgenommen haben.
Eine Figur, die man durch eine Achsenspiegelung auf sich selbst abbilden kann, heißt achsensymmetrisch.
2.Station: Achsensymmetrische Vierecke
5. Aufgabe
In dieser Aufgabe wollen wir herausfinden, wieviel Symmetrieachsen jedes der Vierecke hat.
Ordne den Vierecken ihren Namen und das Bild ihrer Symmetrieachsen zu. Dazu musst du die Bilder mit der linken Maustaste ziehen und fallenlassen, wenn der Hintergrund rot wird. Viel Spaß!
Überprüfe, ob du alle Symmetrieachsen gefunden hast.
Vorlage:Versteckt
Achsensymmetrische Vierecke:
Es gibt fünf achsensymmetrische Vierecke: das Quadrat, das Rechteck, die Raute, den Drachen und das gleichschenklige Trapez.
Dabei besitzen Drachen und Trapez jeweils eine Symmetrieachse, das Rechteck und die Raute zwei und das Quadrat sogar vier.
- 1. Fall: Die Symmetrieachse verläuft durch die gegenüberliegenden Eckpunkte des Vierecks (Drachen, Raute).
- 2. Fall: Die Symmetrieachse geht durch die Mittelpunkte gegenüberliegender, paralleler Seiten eines Vierecks (Rechteck, Trapez).
- Beim Quadrat trifft sowohl Fall 1, als auch Fall 2 zu.
6. Aufgabe
Du kennst jetzt alle achsensymmetrsichen Vierecke und weißt, wieviele Symmetrieachsen sie haben. Kannst du auch folgende Fragen dazu richtig beantworten? Dabei können auch mehrere Antwortmöglichkeiten richtig sein.
Bei welchem Viereck stehen die Symmetrieachsen senkrecht aufeinander? (Raute) (!Trapez) (Rechteck)
Welche Vierecke haben mehr als eine Symmetrieachse?(!Drachen) (Quadrat) (Raute) (!Trapez) (Rechteck)
Die Raute hat ...? (je zwei Paar gleich großer Winkel) (!rechte Winkel) (!ein Paar gleich großer Winkel)
Welches Viereck hat vier gleich lange Seiten?(!Drachen) (Quadrat) (!Rechteck) (Raute)
Bei welchem Viereck verlaufen die Symmetrieachsen durch die Seitenmitten? (Rechteck) (!Raute) (Quadrat) (!Raute)
Hast du alle Fragen richtig beantwortet? Dann geht´s jetzt zur nächsten Station.
3.Station: Achsensymmetrische Dreiecke
Es gibt zwei achsensymmetrische Dreiecke. Mal sehen, ob du herausfindest, wie sie heißen.
7. Aufgabe
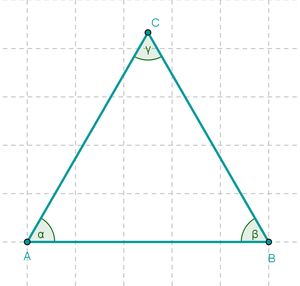
Ziehe am Punkt C. Wann wird das Dreieck achsensymmetrisch? Wieviele Symmetrieachsen hat das Dreieck?
Die Datei [INVALID] wurde nicht gefunden.
Versuche die Fragen richtig zu beantworten! Klicke dabei entweder auf Richtig oder Falsch!
Na kannst du dir denken, wie dieses Dreick heißt?
Hier findest du den Merksatz! Vorlage:Versteckt
8. Aufgabe
Alle achsensymmetrischen Vierecke können durch ihre Diagonalen in gleichschenklige Dreiecke zerlegt werden. Zeichne dir die Vierecke und die Teildreicke in dein Heft. Zähle dann wieviel Dreiecke du in jedem Viereck entdeckst!
Hier findest du die Lösung! Vorlage:Versteckt
9. Aufgabe
Es gibt noch ein achsensymmetrisches Dreieck. Dabei handelt es sich um einen Spezialfall des gleichschenkligen Dreiecks.
Finde die unverdrehte Lösung zu den verdrehten Wörtern! Achte dabei auf Rechtschreibfehler.
Bei diesem Dreieck sind alle drei Seiten gleich lang. Es wird daher gleichseitiges Dreieck genannt.
Dabei können je zwei Seiten des Dreiecks die Schenkel sein. Im gleichseitigen Dreick gibt es daher drei Symmetrieachsen.
Außerdem sind alle drei Winkel gleich groß. Aus der Innenwinkelsumme im Dreieck folgt, dass die Winkel das Maß 60° besitzen.
Konntest du zu allen Wörtern die richtige Lösug finden? Dann weißt du ja jetzt, wie das Dreieck heißt. Super!
Hier findest du den Merksatz! Vorlage:Versteckt
4.Station: Übungen
Übung 1
Hier gibts nochmal ein Memory. Es gehören immer drei Kärtchen zusammen.
Folgende Kategorien sind zu finden:
- achsensymmetrische Verkehrsschilder
- nicht achsensymmetrische Verkehrsschilder
- achsensymmetrische Automarken
- nicht achsensymmetrische Automarken
- achsensymmetrische Gegenstände aus dem Alltag
Drei zusammengehörige Teile zu finden, ist ganz schön schwer, oder?
Übung 2
Zusatzaufgabe
Du kennst bereits achsensymmetrische Dreiecke und Vierecke und deren Symmetrieachsen. Aber wieviel Symmetrieachsen hat eigentlich ein Kreis?
Hier findest du die Lösung! Vorlage:Versteckt