Umfang und Flächeninhalt vom Rechteck: Unterschied zwischen den Versionen
Main>Markus Bergmann Keine Bearbeitungszusammenfassung |
Main>Markus Bergmann Keine Bearbeitungszusammenfassung |
||
| Zeile 22: | Zeile 22: | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
'''Die Fläche A eines Rechtecks mit den Seitenlängen a und b erhält man, wenn man und b multipliziert. | '''Die Fläche A eines Rechtecks mit den Seitenlängen a und b erhält man, wenn man und b multipliziert. | ||
\mathbf {A = a \cdot b} | \mathbf{A = a \cdot b} | ||
<br> | <br> | ||
| | ||
</div> | |||
3. Zeichne vier verschiedene Rechtecke in dein Heft, die alle gleichen Flächeninhalt haben. | 3. Zeichne vier verschiedene Rechtecke in dein Heft, die alle gleichen Flächeninhalt haben. | ||
Version vom 29. Dezember 2008, 22:21 Uhr
Umfang und Flächeninhalt vom Rechteck
==Einführung== Vorlage:Hinweis Zeit
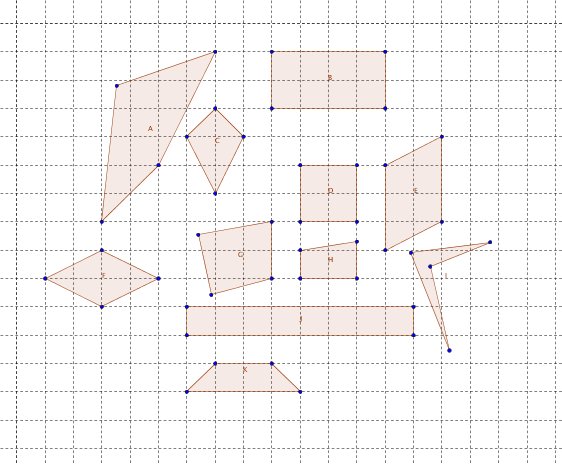
1. Welche Vierecke sind Rechtecke?
2. Schreibe fünf Beispiele von Rechtecken, die man in unserer Umgebung finden kann, in dein Heft.
==Flächeninhalt== Vorlage:Hinweis Zeit
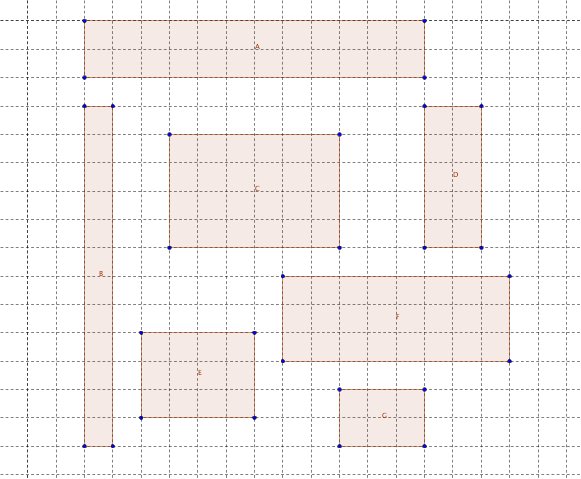
1. Welche der Rechecke haben gleichen Flächeninhalt?
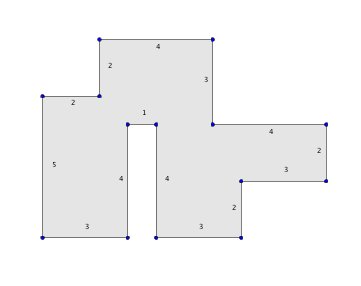
2. Hier handelt es sich zwar nicht um ein Rechteck, kannst du dennoch den Flächeninhalt bestimmen?
Was du dir nun merken kannst.
Die Fläche A eines Rechtecks mit den Seitenlängen a und b erhält man, wenn man und b multipliziert.
\mathbf{A = a \cdot b}
3. Zeichne vier verschiedene Rechtecke in dein Heft, die alle gleichen Flächeninhalt haben.
==Umfang== Vorlage:Hinweis Zeit
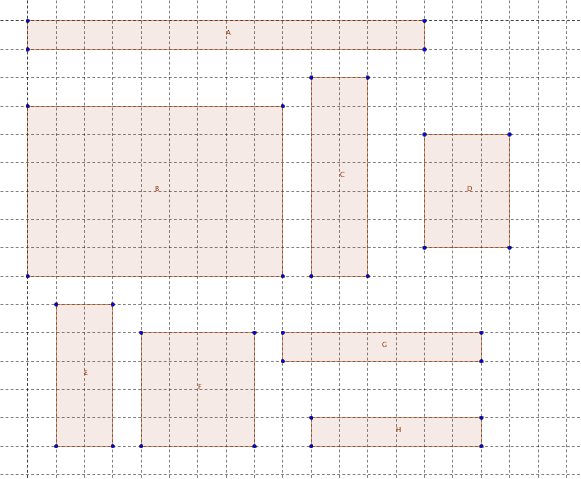
1. Welche der Rechtecke haben gleichen Umfang?
2. Zeichne vier verschiedene Rechtecke in dein Heft, die alle gleichen Umfang haben.
==Gemischte Aufgaben zum Flächeninhalt und Umfang== Vorlage:Hinweis Zeit
1. Wenn du auf diesen Link klickst, kannst du online ein paar Aufgaben zum Flächeninhalt und Umfang bearbeiten.
2. In unteren Bild kannst du die Höhe und Breite des Rechtecks mittels der Schieberegler verändern. Versuche nun das Rechteck so zu verändern, dass der Flächeninhalt und der Umfang des Rechtecks die gleiche Maßzahl haben. Wie viele verschiedene Möglichkeiten findest du?

Schon fertig?
1. Dann versuche die Oberfläche des Würfels zu berechnen (Kantenlänge ist 1 cm).
Weißt du auch, wie lange alle Kanten zusammen sind?
2. Um welchen Faktor ändert sich der Umfang, und um welchen Faktor ändert sich der Flächeninhalt eines Rechtecks, wenn man alle Seitenlängen verdoppelt?
Quiz
Kreuze alle Antwort an, welche deiner Meinung nach richtig sind.