Rechteck - Flächeninhalt und Eigenschaften: Unterschied zwischen den Versionen
Main>Maria Eirich (leerzeilen verändert) |
Main>Maria Eirich Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{| | {| | ||
|{{Lernpfad-M|[[Bild:Rechteck1.jpg|200px|left]]In dieser Unterrichtseinheit finden sich Fragen und Aufgaben rund ums Rechteck | |{{Lernpfad-M|[[Bild:Rechteck1.jpg|200px|left]]In dieser Unterrichtseinheit finden sich Fragen und Aufgaben rund ums Rechteck. Die Formel für den Flächeninhalt wird selbständig erarbeitet und auch eingeübt. Ergebnisse werden im Heft festgehalten. Möglichkeiten zur Differenzierung sind vorgesehen. | ||
<br>'''Voraussetzungen:'''Umfang und die wichtigsten Eigenschaften eines Rechtecks, erste Überlegungen zur Flächenmessung | |||
<br>'''Zeitbedarf:''' etwa 3 Schulstunden | <br>'''Zeitbedarf:''' etwa 3 Schulstunden | ||
<br>'''Material:''' {{pdf|07-03_Test_zum_Lernpfad_Rechteck.pdf|Abschlusstest}} {{pdf|07-03_Test_zum_Lernpfad_RechteckVerb2.pdf|Abschlusstest mit Lösung}} | <br>'''Material:''' {{pdf|07-03_Test_zum_Lernpfad_Rechteck.pdf|Abschlusstest}} {{pdf|07-03_Test_zum_Lernpfad_RechteckVerb2.pdf|Abschlusstest mit Lösung}} | ||
| Zeile 23: | Zeile 24: | ||
:2. Was ist 1 cm² (1 Quadratzentimeter)? | :2. Was ist 1 cm² (1 Quadratzentimeter)? | ||
:3. Veranschauliche deine Überlegungen an Hand einer Zeichnung im Heft. | :3. Veranschauliche deine Überlegungen an Hand einer Zeichnung im Heft. | ||
<br> | |||
<br> | |||
<br> | <br> | ||
==Flächeninhalt eines Rechtecks == | ==Flächeninhalt eines Rechtecks == | ||
| Zeile 54: | Zeile 57: | ||
#Die zwei Diagonalen eines Rechtecks sind ......................................................... | #Die zwei Diagonalen eines Rechtecks sind ......................................................... | ||
</div> | </div> | ||
<br> | |||
<br> | <br> | ||
<br> | <br> | ||
Version vom 14. April 2007, 20:55 Uhr
| Vorlage:Lernpfad-M |
Geometrische Figuren
In der Geometrie gibt es verschiedene Figuren kennen. Welche kennst du bereits?
Klicke auf folgenden Link und versuche, dir die Namen der Figuren zu merken! Eine der Figuren heißt "Deltoid". Dieser Begriff kommt aus Österreich. Welchen Namen kennst du für diese Figur?
Flächenmessung (Wiederholung)
- 1. Informiere dich in folgendem Hefteintrag/Seite 1 wie man Flächen messen kann.
- 2. Was ist 1 cm² (1 Quadratzentimeter)?
- 3. Veranschauliche deine Überlegungen an Hand einer Zeichnung im Heft.
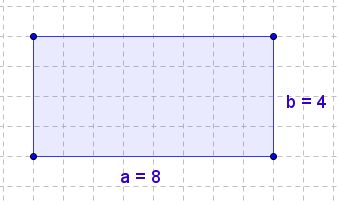
Flächeninhalt eines Rechtecks
|
Weitere Eigenschaften
Welche weiteren Eigenschaften eines Rechtecks kennst du? Mach dir Gedanken zu folgenden Fragen und notiere deine Ergebnisse:
- Wie berechnet man den Umfang eines Rechtecks?
- Wie groß sind die Winkel eines Rechtecks?
- Wie viele Symmetrieachsen hat ein Rechteck?
Übertrage die Sätze in dein Heft und vervollständige sie:
Merke: Eigenschaften des Rechtecks
- Je zwei gegenüberliegende Seiten sind ..............................................................
- Die zwei Diagonalen eines Rechtecks sind .........................................................
Kontrolle der bisherigen Ergebnisse
Vergleiche deine bisherigen Ergebnisse und Vermutungen aus Aufgabe 3 und 4 mit den folgenden Möglichkeiten:
Übungen online!
Hier findest zahlreiche Aufgaben zu Flächeninhalt und Umfang. Gleichzeitig kannst du deine Berechnungen veranschaulichen, indem du mit der Maus den Eckpunkt C verschiebst. Schaffst du es die 195-Punkte-Marke zu überspringen?
Teste dich!
Hausaufgabe
Aufgabe 1:
In einer Streichholzschachtel befinden sich noch 12 Streichhölzer. Jedes einzelne Streichholz ist 5 cm lang.
- Wie viele "Rechtecke" kannst du aus den Streichhölzern legen, wenn du alle verwendest?
- Alle "Rechtecke" haben denselben Umfang. Wie lang ist dieser?
- Bestimme die Flächeninhalte deiner Rechtecke. Welches hat den größten Flächeninhalt?
Quelle: LS5, S.178
Aufgabe 2:
Überlege dir eine interessante Textaufgabe, in dem Flächeninhalt und Umfang vorkommen.
- Notiere die Aufgabenstellung und die Berechnung dazu im Hausheft.
- Wenn du möchtest, kannst du deine Aufgabe auch hier im Wiki veröffentlichen.
Drei Spiele zum Schluss!!
- Es gibt verschiedene Möglichkeiten aus 5 Pentominos ein Quadrat zusammenzusetzen. Finde mindestens eine. Welchen Flächeninhalt hat das "Pentominoquadrat"?
- Mit diesem Memory wiederholst du noch einmal die verschiedenen geometrischen Figuren.
- Hier kannst du Flächen messen und schätzen.