Lineare Funktionen/Station 2/Übung: Unterschied zwischen den Versionen
K (1 Version importiert) |
(Vorlagen angepasst) |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Power-sports-1015688 1920.jpg|right|200px|Bankdrücken]] | |||
'''Übung macht den Meister!''' In dieser Station kannst du dein eben erworbenes oder vertieftes Wissen festigen. Viel Spaß! | |||
{{Aufgabe|'''Übung 5:''' Wie war das jetzt nochmal? | |||
Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen. | |||
}} | |||
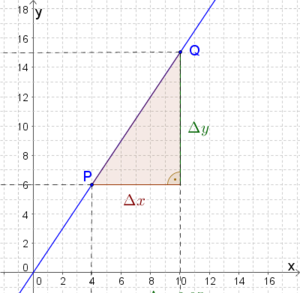
[[Datei:Steigungsdreieck A1.png|300px|Bild zur Aufgabe 1]] | |||
<div class="lueckentext-quiz"> | |||
Die Steigung m berechnet man mithilfe des Steigungsdreiecks. | |||
<math>m=\Delta</math>'''y''' <math>:\Delta </math> '''x''' = ('''y<sub>Q</sub>'''<math>-</math>'''y<sub>P</sub>''')<math>:</math>('''x<sub>Q</sub>'''<math>-</math>'''x<sub>P</sub>''')<math>=</math>('''15'''<math>-</math>'''6''')<math>:</math>('''10'''<math>-</math>'''4''')<math>=</math>'''1,5''' | |||
</ | |||
Die Steigung der dargestellten Geraden ist <math>m=</math>'''1,5''' | Die Steigung der dargestellten Geraden ist <math>m=</math>'''1,5''' | ||
</div> | </div> | ||
{{Aufgabe|'''Übung 6:''' Wie groß ist die Steigung? | |||
[[Datei:Browse-1019848 1920.jpg|right|220px|Buch lesen]] | |||
Schlage bitte dein Mathebuch auf der '''Seite 47''' auf und betrachte in '''Aufgabe 5''' diejenige Gerade, die zu einer proportionalen Funktion passt. Berechne von dieser einen Geraden die Steigung. | |||
* Notiere dein Rechnungen und Überlegung im Übungsheft. | |||
* Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest. | |||
}} | |||
<popup name="Lösung"> | <popup name="Lösung"> | ||
{| | {| | ||
| Zeile 61: | Zeile 41: | ||
<!--> | <!--> | ||
</popup> | </popup> | ||
{{Aufgabe|'''Übung 7:''' Zeichne die Gerade! | |||
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks! | Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks! | ||
a) <math>f(x)=1,5\cdot x</math><br><br>b) <math>g(x)=-\frac{1}{4}\cdot x</math> | |||
}} | |||
<popup name = "Tipp zur a)">Wandle zunächst die Steigung 1,5 in einen Bruch um!</popup> | |||
<popup name="Lösung"> | <popup name="Lösung"> | ||
{| | {| | ||
| Zeile 82: | Zeile 58: | ||
|} | |} | ||
</popup> | </popup> | ||
== Doping für Schnelle == | |||
==Doping für Schnelle== | |||
<span style ="color:blue">Du liegst '''gut in der Zeit?'''</span> [[File:Animated winking Smiley colored.gif|100px|right|Animated winking Smiley colored]] | <span style ="color:blue">Du liegst '''gut in der Zeit?'''</span> [[File:Animated winking Smiley colored.gif|100px|right|Animated winking Smiley colored]] | ||
Dann versuch doch, den armen Radfahrern zu helfen...! | Dann versuch doch, den armen Radfahrern zu helfen...! | ||
{ | {{Aufgabe|'''Für Schnelle - Übung 8: Tour de France!''' | ||
Damit die Radfahrer wissen, wie viel Doping sie zur Tour de France mitnehmen sollen, müssen sie wissen, welche Steigungen im Mittel zu erwarten sind. | |||
Bearbeite dazu die im Übungsheft '''Aufgabe 6 auf Seite 34.''' | |||
}} | |||
Bearbeite dazu die im Übungsheft '''Aufgabe 6 auf Seite 34.''' | Du weißt nicht wie du anfangen sollst? | ||
<popup name="Tipp 1"> | <popup name="Tipp 1"> | ||
"mittlere Steigung" bedeutet dass man annimmt, die Steigung verläuft ''gleichmäßig'' zwischen zwei Punkten. | "mittlere Steigung" bedeutet dass man annimmt, die Steigung verläuft ''gleichmäßig'' zwischen zwei Punkten. | ||
Gleichmäßige Steigung wiederum heißt, du kannst die beiden Punkte mit einer ________ verbinden... | Gleichmäßige Steigung wiederum heißt, du kannst die beiden Punkte mit einer ________ verbinden... | ||
</popup | </popup> | ||
<popup name="Tipp 2"> | <popup name="Tipp 2"> | ||
Wenn du die Punkte mit je einer Geraden verbunden hast, musst du Steigungsdreiecke einzeichnen und damit die Steigung bestimmen. | Wenn du die Punkte mit je einer Geraden verbunden hast, musst du Steigungsdreiecke einzeichnen und damit die Steigung bestimmen. | ||
</popup | </popup> | ||
<popup name="Lösung der Aufgabe"> | |||
Legt man den Koordinatenusrprung in den Punkt A so gilt: | Legt man den Koordinatenusrprung in den Punkt A so gilt: | ||
[[Datei:Bergsteigung Lsg.png|500px|mittlere Steigungen]] | [[Datei:Bergsteigung Lsg.png|500px|mittlere Steigungen]] | ||
</popup | </popup> | ||
{{Frage| | {{Frage| | ||
Musst du alle Längen aus der Zeichnung, die zur Bestimmung der Steigung nötig sind, erst in die realen Längen umrechnen? | Musst du alle Längen aus der Zeichnung, die zur Bestimmung der Steigung nötig sind, erst in die realen Längen umrechnen? | ||
}} | }} | ||
| | [[Datei:Berg Steigung.png|280px|Berg Steigung]] | ||
'''Alles geschafft? Super, dann auf zu Station 3!''' | '''Alles geschafft? Super, dann auf zu Station 3!''' | ||
| | [[Datei:binoculars-1015267_1920.jpg|150px]] | ||
[[../../Station_3|'''...hier geht es weiter''']]'''!''' | |||
{{Lernpfad Lineare Funktionen}} | {{Lernpfad Lineare Funktionen}} | ||
Version vom 8. April 2018, 06:56 Uhr
Übung macht den Meister! In dieser Station kannst du dein eben erworbenes oder vertieftes Wissen festigen. Viel Spaß!
Übung 5: Wie war das jetzt nochmal?
Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.
y x = (yQyP)(xQxP)(156)(104)1,5
Die Steigung der dargestellten Geraden ist 1,5
Übung 6: Wie groß ist die Steigung?
Schlage bitte dein Mathebuch auf der Seite 47 auf und betrachte in Aufgabe 5 diejenige Gerade, die zu einer proportionalen Funktion passt. Berechne von dieser einen Geraden die Steigung.
- Notiere dein Rechnungen und Überlegung im Übungsheft.
- Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.
<popup name="Lösung">
| blaue Gerade: </popup>
Aufgabe Übung 7: Zeichne die Gerade! Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks! a) <popup name = "Tipp zur a)">Wandle zunächst die Steigung 1,5 in einen Bruch um!</popup> <popup name="Lösung">
</popup>
Doping für SchnelleDu liegst gut in der Zeit?Dann versuch doch, den armen Radfahrern zu helfen...! Aufgabe Für Schnelle - Übung 8: Tour de France! Damit die Radfahrer wissen, wie viel Doping sie zur Tour de France mitnehmen sollen, müssen sie wissen, welche Steigungen im Mittel zu erwarten sind. Bearbeite dazu die im Übungsheft Aufgabe 6 auf Seite 34. Du weißt nicht wie du anfangen sollst? <popup name="Tipp 1"> "mittlere Steigung" bedeutet dass man annimmt, die Steigung verläuft gleichmäßig zwischen zwei Punkten. Gleichmäßige Steigung wiederum heißt, du kannst die beiden Punkte mit einer ________ verbinden... </popup> <popup name="Tipp 2"> Wenn du die Punkte mit je einer Geraden verbunden hast, musst du Steigungsdreiecke einzeichnen und damit die Steigung bestimmen. </popup> <popup name="Lösung der Aufgabe"> Legt man den Koordinatenusrprung in den Punkt A so gilt: mittlere Steigungen </popup> Frage Musst du alle Längen aus der Zeichnung, die zur Bestimmung der Steigung nötig sind, erst in die realen Längen umrechnen?
Datei:Binoculars-1015267 1920.jpg
|