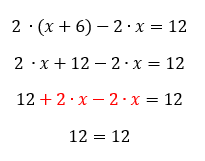Wiederholung: Terme, Termstrukturen und Gleichungen

Zu versteckender Text, ggf. in separatem Template

Das weißt du schon über Terme, Termstrukturen und Gleichungen!

Wir erinnern uns, eine Variable ist eine beliebige Zahl und ein Term ist ein sinnvoller mathematischer Rechenausdruck. Terme können eingliedrig oder mehrgliedrig sein und du kannst sie miteinander addieren, subtrahieren und mulitiplizieren. Bei einer Division spricht man dann von Bruchtermen.

Jeder Term besitzt eine Grob- und eine Feinstruktur. Durch eine genaue Untersuchung des Terms kannst du diese Struktur erkennen.

Eine Gleichung stellt den Zusammenhang von Termen mittels Gleichtheitszeichen "=" dar. Formeln sind allgemein gültige Gleichungen.

Aufgabe 1

Löse folgende Zuordnungsaufgabe. Wenn du die Aufgabe richtig gelöst hast, dann darfst du die Punkte in deine Punktetabelle übertragen. Du bekommst 2 Punkte, wenn du weniger als 3 Versuche benötigst, sonst bekommst du 1 Punkt .

Subtrahiere x vom Dreifachen von y.	3 ⋅ y - x
Multipliziere y mit der Hälfte von x.	y ⋅ (x:2)	(x:2) ⋅ y
Verdopple die Differenz von x und y.	2 ⋅ (x - y)	(x - y) ⋅ 2
Dividiere die Differenz von y und x durch 2.	(y - x):2
Subtrahiere die Hälfte von y von x.	x - y:2
Addiere x zum Doppelten von y.	2 ⋅ y + x	x + 2 ⋅ y

Aufgabe 2: Zaubertrick?

Denke an eine beliebige Zahl. Addiere 6 dazu und verdopple nun deine Zahl. Anschließend subtrahiere das doppelte deiner Zahl. Das Ergebnis ist 12. Wieso klappt das für jede Zahl?
Überlege mit deinem/deiner SitznachbarIn.

Die ausgedachte Zahl kürzt sich raus.

Habt ihr die richtige Lösung gefunden? Das gibt einen Punkt!

Aufgabe 3

In welcher Struktur kann der Term dargestellt werden? Kreuze an! Wenn du die Aufgabe richtig gelöst hast, dann darfst du die Punkte in deine Punktetabelle übertragen. Du bekommst 2 Punkte, wenn du 100 Prozent erreicht hast. Beachte, dass du bei dieser Aufgabe nur einen Versuch hast.

$4a^2 + 8ab$ (A + B) (!A ⋅ B + C) (!A + B ⋅ C) (!A ⋅ [B + C])

$2 \cdot [x^2 - y^2] + [x - y]$ (A + B) (!A + B + C) (A ⋅ B + C) (!A ⋅ [B + C])

$efg + e^2 f + 2$ (A + B + C) (!A ⋅ B + C) (!A ⋅ B ⋅ C) (!A ⋅ [B + C])

$\frac{[a-10] \cdot [a+10]}{10}$ (A ⋅ B) ($\frac{AB}{C}$) () ()