Benutzer:Cloehner/Stochastik Einführungsphase NRW/Baumdiagramme und Pfadregeln: Unterschied zwischen den Versionen
K (F.Bischof verschob die Seite Stochastik Einführungsphase NRW/Baumdiagramme und Pfadregeln nach Benutzer:Cloehner/Stochastik Einführungsphase NRW/Baumdiagramme und Pfadregeln) |
|||
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Glücksspiel= | =Glücksspiel= | ||
| Zeile 17: | Zeile 15: | ||
{{Aufgaben|1|Gib analog zum Beispiel in der Info-Box alle Ergebnisse des zweimaligen Drehens des Glücksrades an. Gib die Ergebnismenge an und bestimme ihre Mächtigkeit. | {{Aufgaben|1.1|Gib analog zum Beispiel in der Info-Box alle Ergebnisse des zweimaligen Drehens des Glücksrades an. Gib die Ergebnismenge an und bestimme ihre Mächtigkeit. | ||
{{Lösung versteckt|Bei <math>(r;b)</math> und <math>(b;r)</math> handelt es sich um unterschiedliche Ergebnisse.|Hinweis anzeigen|Hinweis ausblenden}} | {{Lösung versteckt|Bei <math>(r;b)</math> und <math>(b;r)</math> handelt es sich um unterschiedliche Ergebnisse.|Hinweis anzeigen|Hinweis ausblenden}} | ||
| Zeile 26: | Zeile 24: | ||
{{Aufgaben|2|Formuliere zu den vier möglichen Resultaten passende Ereignisse <math>E_1</math> , <math>E_2</math> , <math>E_3</math> und <math>E_4</math> in Worten und gib die zugehörigen Teilmengen der Ergebnismenge an.}} | {{Aufgaben|1.2|Formuliere zu den vier möglichen Resultaten passende Ereignisse <math>E_1</math> , <math>E_2</math> , <math>E_3</math> und <math>E_4</math> in Worten und gib die zugehörigen Teilmengen der Ergebnismenge an.}} | ||
| Zeile 35: | Zeile 32: | ||
{{Aufgaben|3|Zeichne das Baumdiagramm zum zweimaligen Drehen des Glücksrades. | {{Aufgaben|1.3|Zeichne das Baumdiagramm zum zweimaligen Drehen des Glücksrades. | ||
{{Lösung versteckt|Falls du dich nicht mehr an den genauen Aufbau eines Baumdiagramms erinnerst, recherchiere diesen online oder im Mathematik-Buch.|Tipp 1 anzeigen|Tipp 1 ausblenden}} | {{Lösung versteckt|Falls du dich nicht mehr an den genauen Aufbau eines Baumdiagramms erinnerst, recherchiere diesen online oder im Mathematik-Buch.|Tipp 1 anzeigen|Tipp 1 ausblenden}} | ||
| Zeile 41: | Zeile 38: | ||
{{Lösung versteckt|Gleiche dein Diagramm mit der Lösung ab. Kläre bei eventuellen Abweichungen, ob dein Ergebnis auch eine richtige Lösung darstellt, bzw. wo etwas schiefgelaufen ist. Diskutiere ggf. mit deinem Nachbarn. | {{Lösung versteckt|Gleiche dein Diagramm mit der Lösung ab. Kläre bei eventuellen Abweichungen, ob dein Ergebnis auch eine richtige Lösung darstellt, bzw. wo etwas schiefgelaufen ist. Diskutiere ggf. mit deinem Nachbarn. | ||
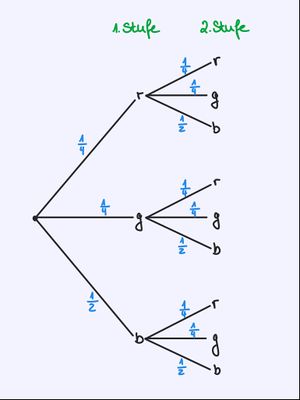
{{Lösung versteckt|[[Datei:Baumdiagramm2.jpg|miniatur]]|Lösung anzeigen|Lösung ausblenden}} | {{Lösung versteckt|[[Datei:Baumdiagramm2.jpg|miniatur|links]]|Lösung anzeigen|Lösung ausblenden}} | ||
|Tipp 2 anzeigen|Tipp 2 ausblenden}} | |Tipp 2 anzeigen|Tipp 2 ausblenden}} | ||
}} | }} | ||
| Zeile 52: | Zeile 48: | ||
{{Aufgaben|4|Berechne die Wahrscheinlichkeiten der vier Ereignisse, die du in Aufgabe 2 formuliert hast. | {{Aufgaben|1.4|Berechne die Wahrscheinlichkeiten der vier Ereignisse, die du in Aufgabe 2 formuliert hast. | ||
{{Lösung versteckt|Die folgende Animation zeigt schrittweise die Vorgehensweise zur Berechnung der Wahrscheinleichkeit des Ereignisses ''<math>E:</math> Der Spieler erhält einen Kino-Gutschein. (Bzw.: Es wird zweimal das rote Feld getroffen.) Übertrage diese Vorgehensweise auf das zweite Ereignis, zu dem ebenfalls nur ein Ergebnis gehört.|Tipp 1 anzeigen|Tipp 1 ausblenden}} | {{Lösung versteckt|Die folgende Animation zeigt schrittweise die Vorgehensweise zur Berechnung der Wahrscheinleichkeit des Ereignisses ''<math>E:</math> Der Spieler erhält einen Kino-Gutschein. (Bzw.: Es wird zweimal das rote Feld getroffen.)'' Übertrage diese Vorgehensweise auf das zweite Ereignis, zu dem ebenfalls nur ein Ergebnis gehört. | ||
[[Datei:Erklärvideo Pfadmultiplikationsregel.mp4|miniatur|links]] | |||
|Tipp 1 anzeigen|Tipp 1 ausblenden}} | |||
{{Lösung versteckt|Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, zu welchem mehrere Ergebnisse gehören, addiert man die Wahrscheinlichkeiten der einzelnen Ergebnisse, die man zuvor wie in Tipp 1 mit der Pfad-Multiplikationsregel berechnen muss.|Tipp 2 anzeigen|Tipp 2 ausblenden}} | |||
{{Lösung versteckt|Mit einer Wahrscheinlichkeit von jeweils <math>\frac{1}{16}</math> erhält man eien Kino-Gutschein oder den Gutschein der Eisdiele. Mit einer Wahrscheinlichkeit von <math>\frac{1}{4}</math> erhält man keinen Preis. Wahrscheinlichkeit für einen Trostpreis: <math>1-\frac{1}{16}-\frac{1}{16}-\frac{1}{4}=\frac{5}{8}</math>|Kontrollösung anzeigen|Kontrollösung ausblenden.}} | |||
}} | }} | ||
{{Aufgaben|1.5|Erkläre unter Verwendung von Fachbegriffen, warum die Wahrscheinlichkeit für einen Trostpreis in Aufgabe 4 mithilfe des Terms aus der Kontrollösung berechnet werden kann.}} | |||
=Baumdiagramme zu verschiedenen Alltagssituationen= | |||
==Bauklötze== | |||
{{Box|Die Sachsituation|Stefans kleiner Bruder spielt mit seinen Bauklötzen. Er hat drei rote, einen grünen und einen blauen Bauklotz. Wie viele verschiedene Türme aus drei Klötzen kann er bauen? Zeichne ein Baumdiagramm. | |||
''Quelle: http://de.serlo.org/29637'' | |||
''Lizenz: https://creativecommons.org/licenses/by-sa/4.0/''|Hervorhebung2}} | |||
{{Aufgaben|2.1|Bearbeite die oben gestellte Aufgabe. Vergleiche dein Ergebnis mit dem eines Mitschülers. Diskutiert eventuelle Unterschiede. | |||
Wenn ihr dem Link zur Quelle der Aufgabe folgt, könnt ihr euch eine Musterlösung ansehen. Vergleicht diese mit euren eigenen Ergebnissen und diskutiert eventuelle Abweichungen.}} | |||
{{Aufgaben|2.2|Berechne die Wahrscheinlichkeit dafür, dass der letzte (obere) Stein des dreistöckigen Turms Blau ist. Gib das zugehörige Ereignis als Menge an. | |||
{{Lösung versteckt|Es handelt sich bei dieser Situation um einen Fall des Ziehens '''ohne Zurücklegen'''. Was bedeutet das für die Wahrscheinlichkeiten der zweiten und dritten Stufe? Recherchiere gegebenenfalls!|Tipp 1 anzeigen|Tipp 1 ausblenden}} | |||
{{Lösung versteckt|Zu Beginn gibt es insgesamt 5 Bauklötze, drei davon sind rot. Was bedeutet das für die Wahrscheinlichkeit dafür, dass Stefans Bruder am Anfang einen roten Bauklotz nimmt? | |||
Überlege für jede Stufe: Wie viele Bauklötze sind insgesamt noch da? Wie viele gibt es noch von den einzelnen Farben? | |||
Wenn zuerst ein roter Klotz verwendet wurde, wirkt sich das auf die Wahrscheinlichkeiten für alle drei Farben auf eine bestimmte Weise aus. Bei einem blauen oder grünen Klotz zu Beginn sieht diese Auswirkung jeweils anders aus.|Tipp 2 anzeigen|Tipp 2 ausblenden}} | |||
}} | |||
==Torwandschießen== | |||
{{Box|Die Sachsituation|Tom, Merle, Theresa und Mark treten beim Torwandschießen gegeneinander an. Tom trifft in 60 % aller Fälle. Bei Merle führt im Durchschnitt jeder zweite Schuss zu einem Treffer. Theresa ist zielsicher und trifft mit einer Wahrscheinlichkeit von 75 %. Jeder dritte von Marks Schüssen führt nicht zu einem Treffer.|Hervorhebung2}} | |||
{{Aufgaben|3.1|Jede der vier Personen gibt einen Schuss auf die Torwand ab. Zeichne zu der Situation ein Baumdiagramm und berechne die Wahrscheinlichkeit für das Ereignis <math>E:</math> ''Mindestens drei der vier Schüsse sind Treffer.'' | |||
{{Lösung versteckt|Das Baumdiagramm sollte aus vier Stufen bestehen, bei denen es jeweils die Ergebnisse „Treffer” und „kein Treffer” gibt.|Tipp 1 anzeigen|Tipp 1 ausblenden}} | |||
{{Lösung versteckt|Die Wahrscheinlichkeiten sind für die einzelnen Stufen unterschiedlich und hängen davon ab, wer gerade auf die Torwand schießt.|Tipp 2 anzeigen|Tipp 2 ausblenden}} | |||
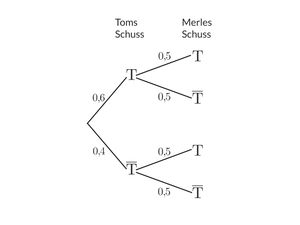
{{Lösung versteckt|Die ersten beiden Stufen des Baumdiagramms könnten wie auf der Abbildung aufgebaut sein: | |||
[[Datei:Baumdiagramm3.jpg|miniatur|links]] | |||
|Tipp 3 anzeigen|Tipp 3 ausblenden}} | |||
}} | |||
{{Aufgaben|3.2|Die vier Personen möchten nun in zwei Teams gegeneinander antreten. Wieder schießt jede Person einmal auf die Torwand. Du kannst also das Baumdiagramm aus Aufgabe 3.1 weiter verwenden. Berechne für die verschiedenen möglichen Konstellationen die Wahrscheinlichkeiten dafür, dass beide Teams gleich viele Treffer erzielen. Bei welcher Team-Zusammensetzung ist der Wettkampf möglichst fair?}} | |||
{{Fortsetzung|weiter=Zufallsgrößen - Wahrscheinlichkeitsverteilungen - Erwartungswerte|weiterlink=Stochastik Einführungsphase NRW/Zufallsgrößen - Wahrscheinlichkeitsverteilungen - Erwartungswerte|vorher=Grundbegriffe der Wahrscheinlichkeitsrechnung|vorherlink=Stochastik Einführungsphase NRW/Grundbegriffe der Wahrscheinlichkeitsrechnung}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie:Sekundarstufe 2]] | |||
[[Kategorie:Wahrscheinlichkeitsrechnung]] | |||
Aktuelle Version vom 23. April 2022, 19:27 Uhr
Glücksspiel
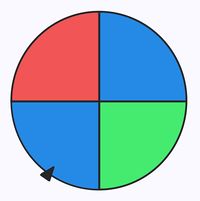
Bei einem Glücksspiel soll das abgebildete Glücksrad zweimal gedreht werden. Wird zweimal das rote Feld gedreht, so erhält der Spieler einen Kino-Gutschein. Falls das Rad zweimal beim grünen Feld stoppt, erhält er einen Gutschein für ein Eiscafé. Einen Trostpreis gibt es, wenn bei den beiden Drehungen unterschiedliche Farben getroffen werden.
Ergebnisse und Ereignisse beim zweimaligen Drehen des Glücksrads
Bei jeder Drehung des Glücksrades kann ein grünes, rotes oder blaues Feld getroffen werden. Die Ergebnismenge des einmaligen Drehens kann also durch beschrieben werden.
Gib analog zum Beispiel in der Info-Box alle Ergebnisse des zweimaligen Drehens des Glücksrades an. Gib die Ergebnismenge an und bestimme ihre Mächtigkeit.
Für den Spieler kann das Glücksspiel vier verschiedene Resultate liefern.
Das Baumdiagramm zum zweimaligen Drehen des Glücksrades
Zum Ermitteln der Wahrscheinlichkeiten zu den Ereignissen, die du in Aufgabe 2 formuliert hast, ist das Erstellen eines Baumdiagramms hilfreich.
Zeichne das Baumdiagramm zum zweimaligen Drehen des Glücksrades.
Die Wahrscheinlichkeiten der verschiedenen Gewinnmöglichkeiten
Mithilfe des Baumdiagramms können die Wahrscheinlichkeiten der verschiedenen Gewinne, die bei dem Glücksspiel eintreten können, nun auf einfachem Wege berechnet werden.
Berechne die Wahrscheinlichkeiten der vier Ereignisse, die du in Aufgabe 2 formuliert hast.
Die folgende Animation zeigt schrittweise die Vorgehensweise zur Berechnung der Wahrscheinleichkeit des Ereignisses Der Spieler erhält einen Kino-Gutschein. (Bzw.: Es wird zweimal das rote Feld getroffen.) Übertrage diese Vorgehensweise auf das zweite Ereignis, zu dem ebenfalls nur ein Ergebnis gehört.
Baumdiagramme zu verschiedenen Alltagssituationen
Bauklötze
Stefans kleiner Bruder spielt mit seinen Bauklötzen. Er hat drei rote, einen grünen und einen blauen Bauklotz. Wie viele verschiedene Türme aus drei Klötzen kann er bauen? Zeichne ein Baumdiagramm.
Quelle: http://de.serlo.org/29637
Bearbeite die oben gestellte Aufgabe. Vergleiche dein Ergebnis mit dem eines Mitschülers. Diskutiert eventuelle Unterschiede.
Wenn ihr dem Link zur Quelle der Aufgabe folgt, könnt ihr euch eine Musterlösung ansehen. Vergleicht diese mit euren eigenen Ergebnissen und diskutiert eventuelle Abweichungen.
Berechne die Wahrscheinlichkeit dafür, dass der letzte (obere) Stein des dreistöckigen Turms Blau ist. Gib das zugehörige Ereignis als Menge an.
Zu Beginn gibt es insgesamt 5 Bauklötze, drei davon sind rot. Was bedeutet das für die Wahrscheinlichkeit dafür, dass Stefans Bruder am Anfang einen roten Bauklotz nimmt?
Überlege für jede Stufe: Wie viele Bauklötze sind insgesamt noch da? Wie viele gibt es noch von den einzelnen Farben?
Wenn zuerst ein roter Klotz verwendet wurde, wirkt sich das auf die Wahrscheinlichkeiten für alle drei Farben auf eine bestimmte Weise aus. Bei einem blauen oder grünen Klotz zu Beginn sieht diese Auswirkung jeweils anders aus.
Torwandschießen
Jede der vier Personen gibt einen Schuss auf die Torwand ab. Zeichne zu der Situation ein Baumdiagramm und berechne die Wahrscheinlichkeit für das Ereignis Mindestens drei der vier Schüsse sind Treffer.