Beschreibende Statistik/Absolute und Relative Häufigkeiten: Unterschied zwischen den Versionen
main>Nina Krämer (Die Seite wurde neu angelegt: „coming soon“) |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (19 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Lernziele:''' | |||
*Sie kennen die Definitionen (und mathematischen Bezeichnungen) der Begriffe | |||
**absolute Häufigkeit und | |||
**relative Häufigkeit einer Merkmalsausprägung. | |||
*Sie können | |||
**die absolute Häufigkeit eines Merkmals und | |||
**die relative Häufigkeit eines Merkmals berechnen. | |||
*Sie können Beobachtungswerte einer Urliste | |||
**als absolute Häufigkeitsverteilung und | |||
**als relative Häufigkeitsverteilung tabellarisch darstellen. | |||
Sie kennen das alles schon? Dann geht es hier direkt zu den Übungen [[Datei:Pfeil 2.gif]] [[#Übungen|Übungen]] | |||
Ansonsten sind Sie hier richtig. | |||
Gerade bei großem Stichprobenumfang ist die Urliste nicht aussagekräftig. Hat man nicht zu viele verschiedene Merkmalsausprägungen, kann man die Häufigkeit festzustellen, mit der ein Merkmal eine bestimmte Ausprägung annimmt. Die Häufigkeit kann in '''absoluten Zahlen''' angegeben werden oder als '''relativer Anteil''' am Umfang der Stichprobe. Denken Sie immer daran, jede Aufbereitung soll die Daten aussagekräftiger machen. Meistens sollen die Daten eine Aussage unterstützen. | |||
Gibt es sehr viele verschiedene Merkmalsausprägungen, so müssen die Merkmalsausprägungen zunächst zu Klassen zusammen gefasst werden. Dazu im nächsten Abschnitt mehr. | |||
<!-- Beispiel absolute und relative Häufigkeiten --> | |||
{| style="color: black; background-color: #FFFFE0;border-left:solid 2px #FFB90F;border-right:solid 2px #FFB90F;border-top:solid 2px #FFB90F;border-bottom:solid 2px #FFB90F;font-size:100%;font-size:100%;" | |||
! align="left" |<u>Beispiel "Alter der Lerngruppe"</u>: | |||
|- | |||
|Die Urliste zum Merkmal "Alter der Lerngruppe" hat einen Stichprobenumfang von <math>n=20</math> und enthält folgende Beobachtungswerte: | |||
::<math>18; 20; 17; 19; 16; 19; 19; 18; 17; 16; 20; 19; 19; 17; 19; 19; 16; 19; 17; 20</math> | |||
Das Merkmal "Alter der Lerngruppe" hat <math>k=5</math> Merkmalsausprägungen, nämlich: | |||
::<math>16; 17; 18; 19; 20</math> | |||
Jetzt lassen sich die absoluten Häufigkeiten leicht durch abzählen berechnen (ideal sind hier Strichlisten), man erhält: | |||
<!-- Tabelle Auswertung Alter der Lerngruppe nach absoluten Häufigkeiten --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
|- | |||
!'''Merkmalsausprägung''' <math>x_i</math>!!<math>16</math>!!<math>17</math>!!<math>18</math>!!<math>19</math>!!<math>20</math>!!Summe | |||
|- | |||
|'''absolute Häufigkeit''' <math>h(x_i)</math>||<math>3</math>||<math>4</math>||<math>2</math>||<math>8</math>||<math>3</math>||<math>20</math> | |||
|} | |||
</div> | |||
<!-- Tabelle Auswertung Alter der Lerngruppe nach absoluten Häufigkeiten --> | |||
|- | |||
|Diese Art die Beobachtungswerte zu präsentieren nennt man '''absolute Häufigkeitsverteilung'''. | |||
Oft interessieren die genauen Zahlen aber gar nicht, sondern es geht nur um Anteile vom Ganzen. Berechnet man aus der absoluten Häufigkeitsverteilung jetzt die relativen Anteile der Merkmalsausprägungen bezogen auf den Stichprobenumfang, so erhält man die folgende Tabelle: | |||
<!-- Tabelle Auswertung Alter der Lerngruppe nach relativen Häufigkeiten --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
|- | |||
!Merkmalsausprägung <math>x_i</math>!!<math>16</math>!!<math>17</math>!!<math>18</math>!!<math>19</math>!!<math>20</math>!!Summe | |||
|- | |||
|absolute Häufigkeit <math>h(x_i)</math>||<math>\frac{3}{20}=</math>||<math>\frac{4}{20}=</math>||<math>\frac{2}{20}=</math>||<math>\frac{8}{20}=</math>||<math>\frac{3}{20}=</math>||<math>1=</math> | |||
|- | |||
|oder als Dezimal- oder Prozentzahl||<math>0,15=15%</math>||<math>0,2=20%</math>||<math>0,1=10%</math>||<math>0,4=40%</math>||<math>0,15=15%</math>||<math>100%</math> | |||
|} | |||
<div> | |||
<!-- Ende Tabelle Auswertung Alter der Lerngruppe nach relativen Häufigkeiten --> | |||
|- | |||
|Diese Art die Beobachtungswerte zu präsentieren nennt man '''relative Häufigkeitsverteilung'''. | |||
Will man nicht mit Brüchen arbeiten, so hat es sich bewährt, Dezimalzahlen mit mindestens 3 Nachkommastellen darzustellen oder alternativ Prozentzahlen mit einer Dezimale. Aber oft sind die Darstellung als Bruch zu bevorzugen, weil es dann keine Rundungsdifferenzen gibt. | |||
|} | |||
<!-- Ende Beispiel absolute und relative Häufigkeiten --> | |||
<!-- Definition absolute und relative Häufigkeiten --> | |||
{{Merke|1=Die <span style="background:yellow">'''absolute Häufigkeit'''</span> <math>H(x_i)</math> gibt die Anzahl aller Merkmalsträger mit dieser Merkmalsausprägung <math>x_i</math> an. | |||
Statt <math>H(x_i)</math> schreibt man auch kurz <math>H_i</math>. | |||
Die <span style="background:yellow">'''relative Häufigkeit'''</span> <math>h(x_i)=\frac{H(x_i)} {n}</math> gibt den Anteil aller Merkmalsträger mit dieser Merkmalsausprägung <math>x_i</math> bezogen auf den Stichprobenumfang <math>n</math> an. | |||
Statt <math>h(x_i)</math> schreibt man auch kurz <math>h_i</math>.}} | |||
<!-- Ende Definition absolute und relative Häufigkeiten --> | |||
<!-- Merksatz absolute und relative Häufigkeiten --> | |||
{{Merke|1=Die Summe der absoluten Häufigkeiten ist immer gleich der Anzahl aller Merkmalsträger, also gleich dem Stichprobenumfang. | |||
Mathematische Kurzschreibweise: | |||
:: <math>\sum_{i=1}^k H(x_i)=n</math> oder noch kürzer <math>\sum_{i=1}^k H_i=n</math>, | |||
wobei <math>k</math> die Anzahl der Merkmalsausprägungen und <math>n</math> den Stichprobenumfang bezeichnen. | |||
Eine Darstellung der Merkmalsausprägungen mit absoluten Häufigkeiten nennt man <span style="background:yellow">'''absolute Häufigkeitsverteilung'''</span>. | |||
Die Summe der relativen Häufigkeiten ist immer gleich 1, also 100 %. | |||
Mathematische Kurzschreibweise: | |||
:: <math>\sum_{i=1}^k h(x_i)=1</math> oder noch kürzer <math>\sum_{i=1}^k h_i=1</math>, | |||
wobei <math>k</math> die Anzahl der Merkmalsausprägungen und <math>n</math> den Stichprobenumfang bezeichnen. | |||
Eine Darstellung der Merkmalsausprägungen mit relativen Häufigkeiten nennt man <span style="background:yellow">'''relative Häufigkeitsverteilung'''</span>.}} | |||
<!-- Ende Merksatz absolute und relative Häufigkeiten --> | |||
[[Datei:Umfrage Eisdiele Urliste.PNG|rechts|Einführung Merkmale und Merkmalsausprägungen]] | |||
<!-- Einführungsbeispiel Teil 5 --> | |||
{| style="color: black; background-color: #FFFAFA;border-left:solid 2px #CD0000;border-right:solid 2px #CD0000;border-top:solid 2px #CD0000;border-bottom:solid 2px #CD0000;font-size:100%;font-size:100%;" | |||
| colspan="4" | | |||
<u>'''Einführungsbeispiel - Teil 5'''<br /></u> | |||
Jetzt kann mit dem nächsten Schritt der Aufbereitung der Umfrage der Eisdiele "Rabe" begonnen werden. Hier soll das Merkmal "Geschlecht" mit absoluten und später mit relativen Häufigkeiten dargestellt werden. | |||
Festgelegt wurde schon <math>x_1=m</math> für männlich und <math>x_2=w</math> für weiblich | |||
<!-- Tabelle Auswertung Geschlecht absolute Häufigkeiten --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
|'''Merkmalsausprägung <math>x_i</math>'''||'''männlich'''||'''weiblich'''||'''Summe''' | |||
|- | |||
|'''absolute Häufigkeit <math>H(x_i)=H_i</math>'''||''' <math>12</math> '''||<math>18</math>||<math>30</math> | |||
|} | |||
<div> | |||
|- | |||
<!-- Ende Auswertung Geschlecht absolute Häufigkeiten --> | |||
| colspan="4" | | |||
Betrachtet man nun die relative Häufigkeit, so erhält man diese, indem jede absolute Häufigkeit durch den Stichprobenumfang dividiert wird: | |||
<!-- Tabelle Auswertung Geschlecht relative Häufigkeiten --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
|'''Merkmalsausprägung <math>x_i</math>'''||'''männlich'''||'''weiblich'''||'''Summe''' | |||
|- | |||
|'''relative Häufigkeit <math>h(x_i)=h_i</math>'''||<math>\frac{12}{30}=0,4=40%</math>||<math>\frac{18}{30}=0,6=60%</math>||<math>1=100%</math> | |||
|} | |||
<div> | |||
<!-- Ende Auswertung Geschlecht relative Häufigkeiten --> | |||
|} | |||
<!-- Ende Einführungsbeispiel Teil 5 --> | |||
{{Aufgabe| | |||
Sie haben Ihr Regelheft mit dem vierten und fünften Merksatz gefüllt. | |||
}} | |||
==Übungen== | |||
<div class="zuordnungs-quiz"> | |||
<big>'''Zuordnung'''</big><br> | |||
Ordnen Sie die mathematischen Bezeichnungen zu. | |||
{| | |||
|Merkmalsausprägungen||<math>x_i</math>||alle verschiedenen Beobachtungswerte eines Merkmals | |||
|- | |||
|Beobachtungswerte||<math>a_i</math>||Einträge zu einem Merkmal in einer Urliste | |||
|- | |||
|absolute Häufigkeit||<math>H_i</math>||<math>H(x_i)</math>||Anzahl mit der eine Merkmalsausprägung vorkommt | |||
|- | |||
|relative Häufigkeit||<math>h_i</math>||<math>h(x_i)</math>||Anteil einer Merkmalsausprägung am Stichprobenumfang | |||
|} | |||
</div> | |||
<!-- Ende Aufgabe 1 --> | |||
<!-- Aufgabe 2 --> | |||
{{Aufgabe|1.4.2 | |||
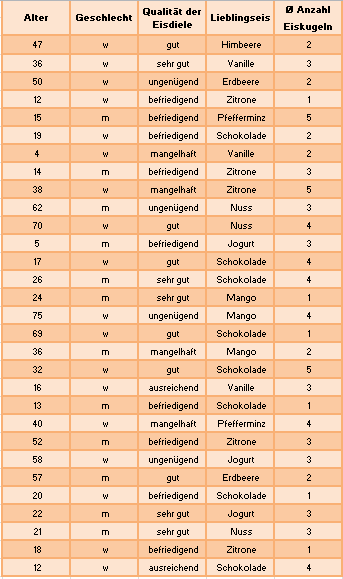
Vervollständigen Sie die Auswertung der Daten, die von der Eisdiele "Rabe" erhoben wurden. Betrachten Sie dazu die Merkmale "Qualität der Eisdiele", "Lieblingseis" und "Durchschnittliche Anzahl Eiskugeln". Bestimmen Sie die zugehörigen absoluten und relativen Häufigkeiten. Ordnen Sie Ihre Ergebnisse übersichtlich in tabellarischer Form für jedes einzelne Merkmal. | |||
Das Merkmal "Alter" zu untersuchen wäre hier nicht zielführend, da es zu viele Merkmalsausprägungen gibt. Dies wird Thema im nächsten Abschnitt. | |||
}} | |||
{{Lösung versteckt| | |||
[[Datei:Loesung Eisdiele.PNG|Beschreibende Statistik - Lösung]] | |||
}} | |||
<!-- Ende Aufgabe 2 --> | |||
<!-- Aufgabe 3 --> | |||
{{Aufgabe|1.4.3 | |||
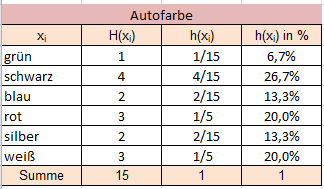
Eine Umfrage zur Lieblingsfarbe des Autos hat folgende Urliste ergeben: blau, grün, schwarz, blau, rot, rot, weiß, silber, silber, weiß, weiß, schwarz, schwarz, schwarz, rot. Legen Sie die Merkmalsausprägungen fest und bestimmen Sie die absolute und relative Häufigkeit der einzelnen Merkmalsausprägungen. | |||
}} | |||
{{Lösung versteckt| | |||
[[Datei:Loesung Autofarbe.PNG|Beschreibende Statistik Lösung Autofarbe]] | |||
}} | |||
<!-- Ende Aufgabe 3 --> | |||
<!-- Aufgabe 4 --> | |||
{{Aufgabe| | |||
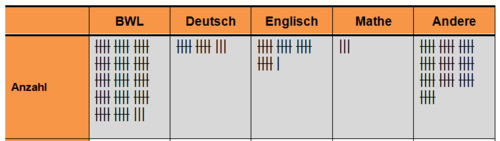
Insgesamt besuchen 135 Schüler und Schülerinnen die Unterstufe der Höheren Handelsschule. Unter ihnen wurde eine Umfrage zur privaten Nutzung des Computers durchgeführt. Es durfte nur der Bereich angekreuzt werden, der am häufigsten genutzt wird. | |||
Bestimmen Sie | |||
* die absolute Häufigkeit und | |||
* die relative Häufigkeit | |||
** als Bruch und | |||
** als Prozentzahl. | |||
[[Datei:1.4 Strichliste.PNG|Strichliste]] | |||
Geben Sie | |||
* die Grundgesamtheit, | |||
* den Stichprobenumfang, | |||
* das Merkmal und | |||
* die Merkmalsausprägungen an. | |||
}} | |||
{{Lösung versteckt|1= | |||
[[Datei:1.4.4 Tabelle L.PNG|Häufigkeiten]] | |||
Die Grundgesamtheit bilden die 135 Schüler und Schülerinnen der Unterstufe der Höheren Handelsschule. | |||
Stichpobenumfang n=105 (die Anzahl aller befragten Schüler und Schülerinnen der Unterstufe der Höheren Handelsschule) | |||
Das untersuchte Merkmal kann kurz so heißen: "Häufigste private Nutzung des Computers" | |||
Die Merkmalsausprägungen lauten: | |||
* Chatten, | |||
* Musikdownload, | |||
* Informationen, | |||
* Games und | |||
* E-Mails.|2=Lösung | |||
}} | |||
<!-- Ende Aufgabe 4 --> | |||
<!-- Aufgabe 5 --> | |||
<div class="lueckentext-quiz"> | |||
Das eigentliche Zählergebnis einer Menge (hier Merkmalsausprägung) nennt man '''absolute Häufigkeit'''. | |||
Den '''Anteil''' von der Gesamtmenge nennt man '''relative Häufigkeit'''. | |||
Die '''Summe''' der relativen Häufigkeiten ergibt, wenn keine Mehrfachnennungen vorliegen, stets '''100 % oder 1''', denn die Summe der '''Anteile''' ergibt ein '''Ganzes'''. | |||
'''Rundungen''' können zu Abweichungen führen. | |||
</div> | |||
<!-- Ende Aufgabe 5 --> | |||
<!-- Aufgabe 6 --> | |||
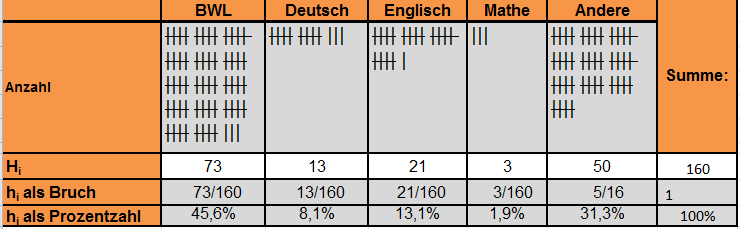
160 Schülerinnen und Schüler der Höheren Handelsschule wurden nach ihrem Lieblingsfach befragt. | |||
Bestimmen Sie | |||
*die absolute Häufigkeit und | |||
*die relative Häufigkeit | |||
**als Bruch und | |||
**als Prozentzahl. | |||
Wie können Sie prüfen, ob Sie richtig gerechnet haben? | |||
[[Datei:1.4.6 Strichliste.PNG|500px|Urliste Beobachtungswerte]] | |||
Geben Sie | |||
*die Grundgesamtheit, | |||
*den Stichprobenumfang, | |||
*das Merkmal und | |||
*die Merkmalsausprägungen an. | |||
{{Lösung versteckt| | |||
[[Datei:1.4.6 Tabelle L.PNG|Lösung]] | |||
Um zu überprüfen, ob man richtig gerechnet hatte, sollte die Tabelle immer eine Summenspalte haben. Die Summe der absoluten Häufigkeiten ist gleich dem Stichprobenumfang. Die Summe der relativen Häufigkeiten ist - bis auf Rundungsdifferenzen - gleich 1. | |||
}} | |||
{{Fortsetzung|weiter=Klassenbildung|weiterlink=Beschreibende Statistik/Klassenbildung}} | |||
{{Beschreibende Statistik}} | |||
Aktuelle Version vom 9. November 2022, 14:32 Uhr
Lernziele:
- Sie kennen die Definitionen (und mathematischen Bezeichnungen) der Begriffe
- absolute Häufigkeit und
- relative Häufigkeit einer Merkmalsausprägung.
- Sie können
- die absolute Häufigkeit eines Merkmals und
- die relative Häufigkeit eines Merkmals berechnen.
- Sie können Beobachtungswerte einer Urliste
- als absolute Häufigkeitsverteilung und
- als relative Häufigkeitsverteilung tabellarisch darstellen.
Sie kennen das alles schon? Dann geht es hier direkt zu den Übungen ![]() Übungen
Übungen
Ansonsten sind Sie hier richtig.
Gerade bei großem Stichprobenumfang ist die Urliste nicht aussagekräftig. Hat man nicht zu viele verschiedene Merkmalsausprägungen, kann man die Häufigkeit festzustellen, mit der ein Merkmal eine bestimmte Ausprägung annimmt. Die Häufigkeit kann in absoluten Zahlen angegeben werden oder als relativer Anteil am Umfang der Stichprobe. Denken Sie immer daran, jede Aufbereitung soll die Daten aussagekräftiger machen. Meistens sollen die Daten eine Aussage unterstützen.
Gibt es sehr viele verschiedene Merkmalsausprägungen, so müssen die Merkmalsausprägungen zunächst zu Klassen zusammen gefasst werden. Dazu im nächsten Abschnitt mehr.
| Beispiel "Alter der Lerngruppe": | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Die Urliste zum Merkmal "Alter der Lerngruppe" hat einen Stichprobenumfang von und enthält folgende Beobachtungswerte:
Das Merkmal "Alter der Lerngruppe" hat Merkmalsausprägungen, nämlich: Jetzt lassen sich die absoluten Häufigkeiten leicht durch abzählen berechnen (ideal sind hier Strichlisten), man erhält:
| |||||||||||||||||||||
| Diese Art die Beobachtungswerte zu präsentieren nennt man absolute Häufigkeitsverteilung.
Oft interessieren die genauen Zahlen aber gar nicht, sondern es geht nur um Anteile vom Ganzen. Berechnet man aus der absoluten Häufigkeitsverteilung jetzt die relativen Anteile der Merkmalsausprägungen bezogen auf den Stichprobenumfang, so erhält man die folgende Tabelle:
| |||||||||||||||||||||
| Diese Art die Beobachtungswerte zu präsentieren nennt man relative Häufigkeitsverteilung.
Will man nicht mit Brüchen arbeiten, so hat es sich bewährt, Dezimalzahlen mit mindestens 3 Nachkommastellen darzustellen oder alternativ Prozentzahlen mit einer Dezimale. Aber oft sind die Darstellung als Bruch zu bevorzugen, weil es dann keine Rundungsdifferenzen gibt. |
Die absolute Häufigkeit gibt die Anzahl aller Merkmalsträger mit dieser Merkmalsausprägung an.
Statt schreibt man auch kurz .
Die relative Häufigkeit gibt den Anteil aller Merkmalsträger mit dieser Merkmalsausprägung bezogen auf den Stichprobenumfang an.
Statt schreibt man auch kurz .
Die Summe der absoluten Häufigkeiten ist immer gleich der Anzahl aller Merkmalsträger, also gleich dem Stichprobenumfang.
Mathematische Kurzschreibweise:
- oder noch kürzer ,
wobei die Anzahl der Merkmalsausprägungen und den Stichprobenumfang bezeichnen.
Eine Darstellung der Merkmalsausprägungen mit absoluten Häufigkeiten nennt man absolute Häufigkeitsverteilung.
Die Summe der relativen Häufigkeiten ist immer gleich 1, also 100 %.
Mathematische Kurzschreibweise:
- oder noch kürzer ,
wobei die Anzahl der Merkmalsausprägungen und den Stichprobenumfang bezeichnen.
Eine Darstellung der Merkmalsausprägungen mit relativen Häufigkeiten nennt man relative Häufigkeitsverteilung.
|
Einführungsbeispiel - Teil 5 Jetzt kann mit dem nächsten Schritt der Aufbereitung der Umfrage der Eisdiele "Rabe" begonnen werden. Hier soll das Merkmal "Geschlecht" mit absoluten und später mit relativen Häufigkeiten dargestellt werden. Festgelegt wurde schon für männlich und für weiblich
| |||||||||||
|
Betrachtet man nun die relative Häufigkeit, so erhält man diese, indem jede absolute Häufigkeit durch den Stichprobenumfang dividiert wird:
| |||||||||||
Sie haben Ihr Regelheft mit dem vierten und fünften Merksatz gefüllt.
Übungen
Zuordnung
Ordnen Sie die mathematischen Bezeichnungen zu.
| Merkmalsausprägungen | alle verschiedenen Beobachtungswerte eines Merkmals | ||
| Beobachtungswerte | Einträge zu einem Merkmal in einer Urliste | ||
| absolute Häufigkeit | Anzahl mit der eine Merkmalsausprägung vorkommt | ||
| relative Häufigkeit | Anteil einer Merkmalsausprägung am Stichprobenumfang |
1.4.2 Vervollständigen Sie die Auswertung der Daten, die von der Eisdiele "Rabe" erhoben wurden. Betrachten Sie dazu die Merkmale "Qualität der Eisdiele", "Lieblingseis" und "Durchschnittliche Anzahl Eiskugeln". Bestimmen Sie die zugehörigen absoluten und relativen Häufigkeiten. Ordnen Sie Ihre Ergebnisse übersichtlich in tabellarischer Form für jedes einzelne Merkmal.
Das Merkmal "Alter" zu untersuchen wäre hier nicht zielführend, da es zu viele Merkmalsausprägungen gibt. Dies wird Thema im nächsten Abschnitt.
1.4.3 Eine Umfrage zur Lieblingsfarbe des Autos hat folgende Urliste ergeben: blau, grün, schwarz, blau, rot, rot, weiß, silber, silber, weiß, weiß, schwarz, schwarz, schwarz, rot. Legen Sie die Merkmalsausprägungen fest und bestimmen Sie die absolute und relative Häufigkeit der einzelnen Merkmalsausprägungen.
Insgesamt besuchen 135 Schüler und Schülerinnen die Unterstufe der Höheren Handelsschule. Unter ihnen wurde eine Umfrage zur privaten Nutzung des Computers durchgeführt. Es durfte nur der Bereich angekreuzt werden, der am häufigsten genutzt wird.
Bestimmen Sie
- die absolute Häufigkeit und
- die relative Häufigkeit
- als Bruch und
- als Prozentzahl.
Geben Sie
- die Grundgesamtheit,
- den Stichprobenumfang,
- das Merkmal und
- die Merkmalsausprägungen an.
Die Grundgesamtheit bilden die 135 Schüler und Schülerinnen der Unterstufe der Höheren Handelsschule.
Stichpobenumfang n=105 (die Anzahl aller befragten Schüler und Schülerinnen der Unterstufe der Höheren Handelsschule)
Das untersuchte Merkmal kann kurz so heißen: "Häufigste private Nutzung des Computers"
Die Merkmalsausprägungen lauten:
- Chatten,
- Musikdownload,
- Informationen,
- Games und
- E-Mails.
Das eigentliche Zählergebnis einer Menge (hier Merkmalsausprägung) nennt man absolute Häufigkeit.
Den Anteil von der Gesamtmenge nennt man relative Häufigkeit.
Die Summe der relativen Häufigkeiten ergibt, wenn keine Mehrfachnennungen vorliegen, stets 100 % oder 1, denn die Summe der Anteile ergibt ein Ganzes.
Rundungen können zu Abweichungen führen.
160 Schülerinnen und Schüler der Höheren Handelsschule wurden nach ihrem Lieblingsfach befragt.
Bestimmen Sie
- die absolute Häufigkeit und
- die relative Häufigkeit
- als Bruch und
- als Prozentzahl.
Wie können Sie prüfen, ob Sie richtig gerechnet haben?
Geben Sie
- die Grundgesamtheit,
- den Stichprobenumfang,
- das Merkmal und
- die Merkmalsausprägungen an.
Um zu überprüfen, ob man richtig gerechnet hatte, sollte die Tabelle immer eine Summenspalte haben. Die Summe der absoluten Häufigkeiten ist gleich dem Stichprobenumfang. Die Summe der relativen Häufigkeiten ist - bis auf Rundungsdifferenzen - gleich 1.
Lernpfad Beschreibende Statistik
- Grundbegriffe
- Graphische Darstellungen von Häufigkeitsverteilungen
- Lagemaße
(arithmetisches Mittel, Modus, Median) - Streuungsmaße
(mittlere absolute Abweichung, mittlere quadratische Abweichung, Standardabweichung) - Einsatz des Taschenrechners
(Bedienung Casio fx-991DE PLUS)