Zentrische Streckung/Abbildung durch zentrische Streckung/3.Station: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Michael Schuster K (hat „Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/3.Station“ nach „Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/3.Station“ verschoben: Lernpfad fertig) |
Keine Bearbeitungszusammenfassung |
||
| (15 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken | |||
|{{Abbildungen durch zentrische Streckung}} | |||
|Lernschritte einblenden | |||
|Lernschritte ausblenden | |||
}} | |||
==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors== | ==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors== | ||
Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke | |||
Geometrisch bedeutet dies für einen beliebigen Punkt P: <math> \overline{ZP'} = \ | {{Box|1= Wie lang ist die Strecke <math> \overline{P'Q'} </math> im Verhältnis zur Strecke <math> \overline{PQ} </math>|2= | ||
Daraus folgt: <math>\ | Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke <math>\vert k \vert </math>-mal so lang wie die Urbildstrecke.<br> | ||
Geometrisch bedeutet dies für einen beliebigen Punkt P: <math> \overline{ZP'} = \vert k \vert \cdot \overline{ZP}</math><br> | |||
Daraus folgt: <math>\vert k \vert = {\overline{ZP'}\over\overline{ZP}}</math><br> | |||
<br> | <br> | ||
Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden. <br> | Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden. <br> | ||
Ziehe dafür den richtigen Ausdruck in die passende Lücke:<br> | Ziehe dafür den richtigen Ausdruck in die passende Lücke:<br> | ||
<div | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
[[Bild:Porzelt_Streckenlänge.jpg]] | |||
</div> | |||
<div class="width-1-2"> | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
< | <math> \overline{ZP'} = \vert k \vert \cdot \overline{ZP} </math> und <math> \overline{ZQ'} = \vert k \vert \cdot \overline{ZQ} </math> | ||
<math>\Rightarrow | <math> \overline{PQ} = \overline{ZQ} - \overline{ZP} </math> und <math> \overline{P'Q'} = \overline{ZQ'} - \overline{ZP'} </math> | ||
<math>\Rightarrow | |||
<math>\Rightarrow | <math>\Rightarrow \overline{P'Q'} = </math> '''<math> \vert k \vert </math>''' <math> \cdot \overline{ZQ} - \vert k \vert \cdot </math> '''<math> \overline{ZP}</math>''' | ||
<math>\Rightarrow \overline{P'Q'} = \vert k \vert \cdot (</math>'''<math> \overline{ZQ} </math>''' - '''<math> \overline{ZP}</math>''') | |||
<math>\Rightarrow \overline{P'Q'} = \vert k \vert \cdot </math> '''<math> \overline{PQ}</math>''' | |||
</div> | </div> | ||
</div> | </div> | ||
</div> | |||
|3=Arbeitsmethode}} | |||
<br> | <br> | ||
[[Bild:Porzelt_lobenderPanto3.jpg]] | [[Bild:Porzelt_lobenderPanto3.jpg]] | ||
<br> | <br> | ||
{{Fortsetzung|weiter=Zusammenfassung|weiterlink=../4.Station}} | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 15:52 Uhr
3. Station: Berechnung der Streckenlängen und des Streckungsfaktors
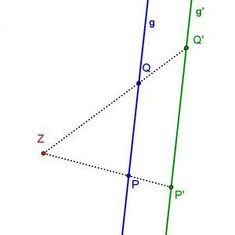
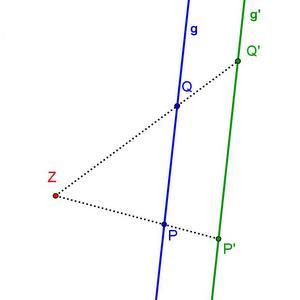
Wie lang ist die Strecke im Verhältnis zur Strecke
Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke -mal so lang wie die Urbildstrecke.
Geometrisch bedeutet dies für einen beliebigen Punkt P:
Daraus folgt:
Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden.
Ziehe dafür den richtigen Ausdruck in die passende Lücke: