Benutzer:Cloehner/Differentialrechnung/Extrempunkte berechnen

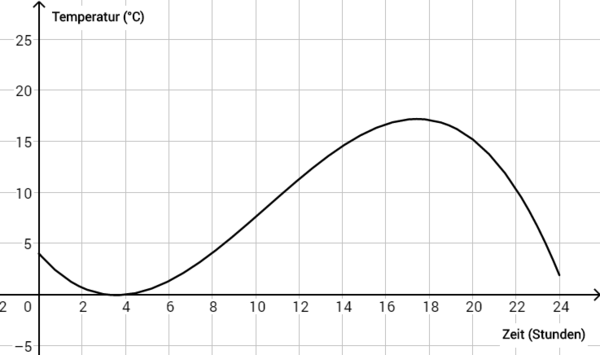
Betrachte die Abbildung zum Temperaturverlauf an einem Herbsttag. Wann ist die Temperatur am niedrigsten? Wann ist sie am höchsten?

Temperaturverlauf an einem Herbsttag

In diesem Abschnitt sollst du herausfinden, wie Hoch- und Tiefpunkte einer ganzrationalen Funktion berechnet werden können. Du wirst zunächst dein Wissen über die Zusammenhänge zwischen dem Graphen einer Funktion und dem ihrer Ableitung vertiefen und daraus Kriterien für Extremstellen entwickeln. Anschließend sollst du diese Kriterien auf konkrete Funktionen anwenden.

Kriterien für Extremstellen

Aufgabe 1

Finde mit einem der folgenden Applets heraus, wie mithilfe der ersten Ableitung einer Funktion herausgefunden werden kann, an welchen Stellen Extrempunkte vorliegen. Das erste Applet lässt dir mehr Raum für eigene Überlegungen, das zweite bietet mehr Hilfe. Entscheide selbst, welches du verwenden möchtest.

Leitfragen für die Erkundung: Wie verläuft die erste Ableitung in der Umgebung einer Maximalstelle, einer Minimalstelle oder allgemeiner einer Extremstelle? Wie sieht es in der Umgebung des x-Wertes eines Sattelpunktes aus?

Variante 1: Viel Raum für eigene Überlegungen

Variante 2: Mit Unterstützung

Hier kannst du dir für das lokale Maximum eine Schritt-für-Schritt-Anleitung anzeigen lassen. Übertrage diese Schritte auf das lokale Minimum und den Sattelpunkt.

Aufgabe 2

Überprüfe mit dem folgenden Lückentext, ob du die wesentlichen Zusammenhänge herausgefunden hast.

Rechnerisches Bestimmen von Extrempunkten

Aufgabe 3

Erläutere den Zusammenhang zwischen den Kriterien, die du soeben erarbeitet hast, und der Vorgehensweise in Beispiel 1 auf Seite 92 (Lambacher Schweizer, Einführungsphase (2014))

Aufgabe 4

Bearbeite Aufgabe 2 a, d und g auf Seite 93. Überprüfe deine Ergebnisse mit GeoGebra oder dem GTR.

Aufgabe 5

Bearbeite Aufgabe 4 aus Seite 93.