Benutzer:Maria Eirich/Box mit Tabelle: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 188: | Zeile 188: | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"> <pre><div class="mw-collapsible mw-collapsed" data-expandtext="Lösung" data-collapsetext="verbergen"> S(1|1)</div></pre> </div> | <div class="width-1-2"> <pre><div class="mw-collapsible mw-collapsed" data-expandtext="Lösung" data-collapsetext="verbergen"> S(1|1)</div></pre> </div> | ||
<div class="width-1-2"><div class="mw-collapsible mw-collapsed" data-expandtext=" | <div class="width-1-2"><div class="mw-collapsible mw-collapsed" data-expandtext="Lösung" data-collapsetext="verbergen"> | ||
S(1|1)</div></div> | S(1|1)</div></div> | ||
</div> | </div> | ||
| Zeile 198: | Zeile 198: | ||
<div class="width-1-2"><pre>{{Lösung versteckt|1=<math>y=(x-1)^2+1</math>}}</pre> </div> | <div class="width-1-2"><pre>{{Lösung versteckt|1=<math>y=(x-1)^2+1</math>}}</pre> </div> | ||
<div class="width-1-2">{{Lösung versteckt|1=<math>y=(x-1)^2+1</math>}}</div> | <div class="width-1-2">{{Lösung versteckt|1=<math>y=(x-1)^2+1</math>}}</div> | ||
</div> | </div> | ||
==Boxen und Lösungen verstecken mit '''|1=... |2=... |3=...'''== | |||
==Boxen und Lösungen verstecken mit ''' | |||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"><pre>{{Lösung versteckt|1= | <div class="width-1-2"><pre>{{Lösung versteckt|1= | ||
| Zeile 235: | Zeile 230: | ||
|3=Arbeitsmethode}}</div> | |3=Arbeitsmethode}}</div> | ||
</div> | </div> | ||
Aktuelle Version vom 25. Januar 2020, 21:33 Uhr
Box mit Tabelle
Finde Werte für a, d und e, so dass die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.
Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben.
| Hintergrundbild | Lösungsvorschlag | Parameter a | Parameter d | Parameter e |
|---|---|---|---|---|
| Angry Birds | -0.15 ≤ a ≤ -0.13 | 6.80 ≤ d ≤ 7.20 | 4.70 ≤ e ≤ 5.00 | |
| Golden Gate Bridge | 0.03 ≤ a ≤ 0.05 | 5.00 ≤ d ≤ 6.40 | 0.80 ≤ e ≤ 1.10 | |
| Springbrunnen | -0.40 ≤ a ≤ -0.30 | 4.70 ≤ d ≤ 5.00 | 5.10 ≤ e ≤ 5.50 | |
| Elbphilharmonie (Bogen links) | 0.33 ≤ a ≤ 0.47 | 2.40 ≤ d ≤ 2.60 | 4.25 ≤ e ≤ 4.40 | |
| Elbphilharmonie (Bogen mitte) | 0.30 ≤ a ≤ 0.36 | 5.70 ≤ d ≤ 6.00 | 3.20 ≤ e ≤ 3.60 | |
| Elbphilharmonie (Bogen rechts) | 0.18 ≤ a ≤ 0.27 | 9.30 ≤ d ≤ 9.50 | 3.55 ≤ e ≤ 3.65 | |
| Gebirgsformation | -0.30 ≤ a ≤ -0.10 | 5.10 ≤ d ≤ 5.70 | 2.10 ≤ e ≤ 2.50 | |
| Motorrad-Stunt | -0.10 ≤ a ≤ -0.04 | 7.30 ≤ d ≤ 8.10 | 5.70 ≤ e ≤ 6.20 | |
| Basketball | -0.35 ≤ a ≤ -0.29 | 6.20 ≤ d ≤ 6.80 | 6.20 ≤ e ≤ 6.70 |
{{Box
|Aufgabe 1
|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 9)''' [[Datei:Notepad-117597.svg|right|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].
Finde Werte für a, d und e, so dass <math>f(x)</math> die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.
{{Lösung versteckt|1=Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben.
{{{!}} class="wikitable"
{{!}}-
! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter d !! Parameter e
{{!}}-
{{!}} Angry Birds {{!}}{{!}} <math>f(x)=-0.13(x-7)^2+4.85</math> {{!}}{{!}} -0.15 ≤ a ≤ -0.13 {{!}}{{!}} 6.80 ≤ d ≤ 7.20 {{!}}{{!}} 4.70 ≤ e ≤ 5.00
{{!}}-
{{!}} Golden Gate Bridge {{!}}{{!}} <math>f(x)=0.04(x-5.7)^2+1</math> {{!}}{{!}} 0.03 ≤ a ≤ 0.05 {{!}}{{!}} 5.00 ≤ d ≤ 6.40 {{!}}{{!}} 0.80 ≤ e ≤ 1.10
{{!}}-
{{!}} Springbrunnen {{!}}{{!}} <math>f(x)=-0.33(x-4,85)^2+5.3</math> {{!}}{{!}} -0.40 ≤ a ≤ -0.30 {{!}}{{!}} 4.70 ≤ d ≤ 5.00 {{!}}{{!}} 5.10 ≤ e ≤ 5.50
{{!}}-
{{!}} Elbphilharmonie (Bogen links) {{!}}{{!}} <math>f(x)=0.40(x-2,50)^2+4.35</math> {{!}}{{!}} 0.33 ≤ a ≤ 0.47 {{!}}{{!}} 2.40 ≤ d ≤ 2.60 {{!}}{{!}} 4.25 ≤ e ≤ 4.40
{{!}}-
{{!}} Elbphilharmonie (Bogen mitte) {{!}}{{!}} <math>f(x)=0.33(x-5.85)^2+3.4</math> {{!}}{{!}} 0.30 ≤ a ≤ 0.36 {{!}}{{!}} 5.70 ≤ d ≤ 6.00 {{!}}{{!}} 3.20 ≤ e ≤ 3.60
{{!}}-
{{!}} Elbphilharmonie (Bogen rechts) {{!}}{{!}} <math>f(x)=0.22(x-9,40)^2+3.60</math> {{!}}{{!}} 0.18 ≤ a ≤ 0.27 {{!}}{{!}} 9.30 ≤ d ≤ 9.50 {{!}}{{!}} 3.55 ≤ e ≤ 3.65
{{!}}-
{{!}} Gebirgsformation {{!}}{{!}} <math>f(x)=-0.2(x-5.4)^2+2.3</math> {{!}}{{!}} -0.30 ≤ a ≤ -0.10 {{!}}{{!}} 5.10 ≤ d ≤ 5.70 {{!}}{{!}} 2.10 ≤ e ≤ 2.50
{{!}}-
{{!}} Motorrad-Stunt {{!}}{{!}} <math>f(x)=-0.07(x-7.7)^2+5.95</math> {{!}}{{!}} -0.10 ≤ a ≤ -0.04 {{!}}{{!}} 7.30 ≤ d ≤ 8.10 {{!}}{{!}} 5.70 ≤ e ≤ 6.20
{{!}}-
{{!}} Basketball {{!}}{{!}} <math>f(x)=-0.32(x-6.5)^2+6.45</math> {{!}}{{!}} -0.35 ≤ a ≤ -0.29 {{!}}{{!}} 6.20 ≤ d ≤ 6.80 {{!}}{{!}} 6.20 ≤ e ≤ 6.70
{{!}}}
|2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}}
|Arbeitsmethode
}}
Tabelle mit div-Container
Aufgabe 1
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 9) .Finde Werte für a, d und e, so dass die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.
Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben.
| Hintergrundbild | Lösungsvorschlag | Parameter a | Parameter d | Parameter e |
|---|---|---|---|---|
| Angry Birds | -0.15 ≤ a ≤ -0.13 | 6.80 ≤ d ≤ 7.20 | 4.70 ≤ e ≤ 5.00 | |
| Golden Gate Bridge | 0.03 ≤ a ≤ 0.05 | 5.00 ≤ d ≤ 6.40 | 0.80 ≤ e ≤ 1.10 | |
| Springbrunnen | -0.40 ≤ a ≤ -0.30 | 4.70 ≤ d ≤ 5.00 | 5.10 ≤ e ≤ 5.50 | |
| Elbphilharmonie (Bogen links) | 0.33 ≤ a ≤ 0.47 | 2.40 ≤ d ≤ 2.60 | 4.25 ≤ e ≤ 4.40 | |
| Elbphilharmonie (Bogen mitte) | 0.30 ≤ a ≤ 0.36 | 5.70 ≤ d ≤ 6.00 | 3.20 ≤ e ≤ 3.60 | |
| Elbphilharmonie (Bogen rechts) | 0.18 ≤ a ≤ 0.27 | 9.30 ≤ d ≤ 9.50 | 3.55 ≤ e ≤ 3.65 | |
| Gebirgsformation | -0.30 ≤ a ≤ -0.10 | 5.10 ≤ d ≤ 5.70 | 2.10 ≤ e ≤ 2.50 | |
| Motorrad-Stunt | -0.10 ≤ a ≤ -0.04 | 7.30 ≤ d ≤ 8.10 | 5.70 ≤ e ≤ 6.20 | |
| Basketball | -0.35 ≤ a ≤ -0.29 | 6.20 ≤ d ≤ 6.80 | 6.20 ≤ e ≤ 6.70 |
<div class="box arbeitsmethode">
== Aufgabe 1 ==
'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 9)''' [[Datei:Notepad-117597.svg|right|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].
Finde Werte für a, d und e, so dass <math>f(x)</math> die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.
<div class="mw-collapsible mw-collapsed" data-expandtext="Lösungsvorschläge anzeigen" data-collapsetext="Lösungsvorschläge verbergen">
Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben.
{| class="wikitable"
|-
! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter d !! Parameter e
|-
| Angry Birds || <math>f(x)=-0.13(x-7)^2+4.85</math> || -0.15 ≤ a ≤ -0.13 || 6.80 ≤ d ≤ 7.20 || 4.70 ≤ e ≤ 5.00
|-
| Golden Gate Bridge || <math>f(x)=0.04(x-5.7)^2+1</math> || 0.03 ≤ a ≤ 0.05 || 5.00 ≤ d ≤ 6.40 || 0.80 ≤ e ≤ 1.10
|-
| Springbrunnen || <math>f(x)=-0.33(x-4,85)^2+5.3</math> || -0.40 ≤ a ≤ -0.30 || 4.70 ≤ d ≤ 5.00 || 5.10 ≤ e ≤ 5.50
|-
| Elbphilharmonie (Bogen links) || <math>f(x)=0.40(x-2,50)^2+4.35</math> || 0.33 ≤ a ≤ 0.47 || 2.40 ≤ d ≤ 2.60 || 4.25 ≤ e ≤ 4.40
|-
| Elbphilharmonie (Bogen mitte) || <math>f(x)=0.33(x-5.85)^2+3.4</math> || 0.30 ≤ a ≤ 0.36 || 5.70 ≤ d ≤ 6.00 || 3.20 ≤ e ≤ 3.60
|-
| Elbphilharmonie (Bogen rechts) || <math>f(x)=0.22(x-9,40)^2+3.60</math> || 0.18 ≤ a ≤ 0.27 || 9.30 ≤ d ≤ 9.50 || 3.55 ≤ e ≤ 3.65
|-
| Gebirgsformation || <math>f(x)=-0.2(x-5.4)^2+2.3</math> || -0.30 ≤ a ≤ -0.10 || 5.10 ≤ d ≤ 5.70 || 2.10 ≤ e ≤ 2.50
|-
| Motorrad-Stunt || <math>f(x)=-0.07(x-7.7)^2+5.95</math> || -0.10 ≤ a ≤ -0.04 || 7.30 ≤ d ≤ 8.10 || 5.70 ≤ e ≤ 6.20
|-
| Basketball || <math>f(x)=-0.32(x-6.5)^2+6.45</math> || -0.35 ≤ a ≤ -0.29 || 6.20 ≤ d ≤ 6.80 || 6.20 ≤ e ≤ 6.70
|}
</div></div>
Warum hier kein Fehler trotz Box
Die Steigung einer Geraden bestimmt man mithilfe eines Steigungsdreiecks.
- Wähle zwei beliebige Punkte P und Q auf der Geraden aus, am besten so, dass man die Koordinaten gut ablesen kann.
- Lege das Steigungsdreieck in diesen Punkten an die Gerade an.
- Berechne die Steigung m:
Unterscheide drei Fälle:
{{Box|1=Merke|2=
Die Steigung einer Geraden bestimmt man mithilfe eines '''Steigungsdreiecks'''.
*Wähle zwei ''beliebige'' Punkte P und Q auf der Geraden aus, am besten so, dass man die Koordinaten gut ablesen kann.
*Lege das Steigungsdreieck in diesen Punkten an die Gerade an.
*Berechne die Steigung m:
<math>m=\frac{\Delta y}{\Delta x}=\frac{y_Q - y_P}{x_Q - x_P}</math>
'''Unterscheide drei Fälle''':
{{3Spalten|
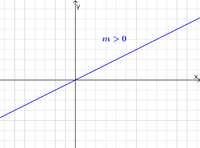
<math>m>0 </math> Gerade steigt nach rechts an
[[Datei:Steigung positiv.png|200px|Steigung positiv]]
|
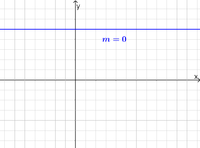
<math>m=0 </math> Gerade parallel zur x-Achse
[[Datei:Steigung Null.png|200px|Steigung Null]]
|
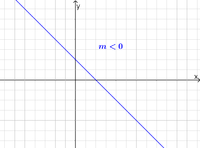
<math>m<0</math> Gerade fällt nach rechts ab
[[Datei:Steigung negativ.png|200px|Steigung negativ]]
}}
|3=Merksatz}}
Beispiele zu Lösung verstecken
<div class="mw-collapsible mw-collapsed" data-expandtext="Lösung" data-collapsetext="verbergen"> S(1|1)</div>
{{Lösung versteckt|1=S(1{{!}}1)}} {{Lösung versteckt|1=<math>y=(x-1)^2+1</math>}} Boxen und Lösungen verstecken mit |1=... |2=... |3=...
{{Lösung versteckt|1=
#<span style="color: red">'''a = - 1; b = -3; c = 2'''</span>
#<span style="color: blue">Scheitel von f: '''S(-3/-2)'''</span>
#<span style="color: green">c verschiebt den Scheitel für '''c > 0 nach oben''' und für '''c < 0 nach unten'''</span>
}}- a = - 1; b = -3; c = 2
- Scheitel von f: S(-3/-2)
- c verschiebt den Scheitel für c > 0 nach oben und für c < 0 nach unten
{{Box|1=Aufgabe 3|2=
Untersuche nun die Funktionen f mit '''f(x) = 1,5x<sup>2</sup> + 9x + 11,5''' und g mit '''g(x) = - 0,5x<sup>2</sup> + x + 2,5'''
#Zeichne mit Hilfe einer Wertetabelle die Graphen G<sub>f</sub> und G<sub>g</sub> in ein gemeinsames Koordinatensystem.
#Gib die Koordinaten der beiden Scheitel S<sub>f</sub> und S<sub>g</sub> an.
#Vergleiche die beiden Parabeln mit der Normalparabel.
|3=Arbeitsmethode}} Untersuche nun die Funktionen f mit f(x) = 1,5x2 + 9x + 11,5 und g mit g(x) = - 0,5x2 + x + 2,5
- Zeichne mit Hilfe einer Wertetabelle die Graphen Gf und Gg in ein gemeinsames Koordinatensystem.
- Gib die Koordinaten der beiden Scheitel Sf und Sg an.
- Vergleiche die beiden Parabeln mit der Normalparabel.