Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Nullstellen bestimmen/Ausklammern: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
__NOTOC__ | __NOTOC__ | ||
==Station | ==Station 1: Nullstellen bestimmen durch Ausklammern (Faktorisieren)== | ||
<br> | <br> | ||
| Zeile 28: | Zeile 28: | ||
<br><br> | <br><br> | ||
== | ==Arbeitsblatt studieren== | ||
{{Box|1=Aufgabe|2= | {{Box|1=Aufgabe|2= | ||
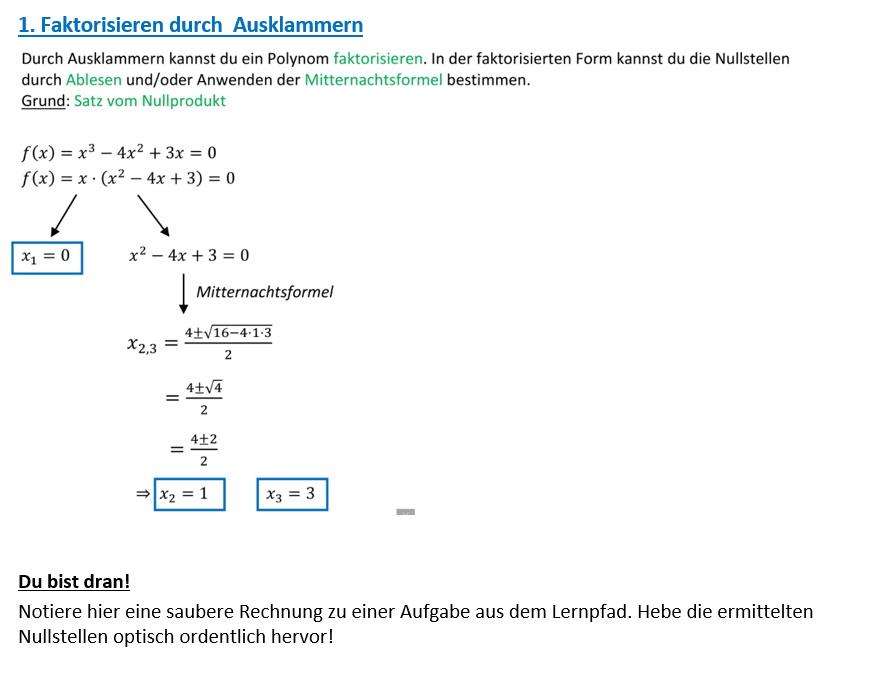
Lies dir im Skript den Abschnitt "1. Faktorisieren durch Ausklammern aufmerksam durch! Bearbeite den gestellten Arbeitsauftrag sauber und ordentlich!'''<br><br> | |||
[[Datei: | [[Datei:Ausklammern.png|300px|center|Hefteintrag Ausklammern|gerahmt]]|3=Arbeitsmethode}} | ||
<br><br> | <br><br> | ||
| Zeile 37: | Zeile 37: | ||
==Teste dich!== | ==Teste dich!== | ||
{{Box|Übung|Übernimm folgende Terme in dein '''Heft''', klammere aus und bestimme die Nullstellen!<br> Arbeite '''absolut übersichtlich und ordentlich'''. Hebe die '''Nullstellen mit Farbe''' hervor!|Üben}} | {{Box|Übung|Übernimm folgende Terme in dein '''Heft''', klammere aus und bestimme die Nullstellen!<br> Arbeite '''absolut übersichtlich und ordentlich'''. Hebe die '''Nullstellen mit Farbe''' hervor!|Üben}} | ||
| Zeile 43: | Zeile 42: | ||
{{Lösung versteckt|1= <math> f(x)=x^3-4x^2 = x^2 (x-4) \text{ mit den Nullstellen }x_1=0 \text{ und } x_2=4</math>|2= Lösung anzeigen|3= Lösung verbergen}} | {{Lösung versteckt|1= <math> f(x)=x^3-4x^2 = x^2 (x-4) \text{ mit den Nullstellen }x_1=0 \text{ und } x_2=4</math>|2= Lösung anzeigen|3= Lösung verbergen}} | ||
| Zeile 68: | Zeile 66: | ||
{{Fortsetzung|weiter=Weiter|weiterlink=../3. Faktorisieren von Polynomen}} | {{Fortsetzung|weiter=Weiter|weiterlink=../3. Faktorisieren von Polynomen}} | ||
[[Kategorie:Keine Kategorie]] | |||
[[Kategorie: | |||
Aktuelle Version vom 23. April 2022, 17:59 Uhr
Station 1: Nullstellen bestimmen durch Ausklammern (Faktorisieren)
Wiederholung - nur falls nötig...
Du solltest mit dem Prinzip des Ausklammerns gut vertraut sein. Falls nicht, schaue dir vorsichtshalber folgendes Video an.
Informiere dich!
In diesem Video wird dir gezeigt, in welchen Fällen das Prinzip des Ausklammern möglich ist, und wie du damit im Anschluss die Nullstellen berechnen kannst.
Arbeitsblatt studieren
Aufgabe
Teste dich!
Übung
Übernimm folgende Terme in dein Heft, klammere aus und bestimme die Nullstellen!
Arbeite absolut übersichtlich und ordentlich. Hebe die Nullstellen mit Farbe hervor!
Arbeite absolut übersichtlich und ordentlich. Hebe die Nullstellen mit Farbe hervor!
Ausklammern ist geschafft! Weiter geht's mit dem Faktorisieren von Polynomen :)