Textaufgaben/Zahlenrätsel

Textaufgaben

• Wiederholung Gleichungen lösen
• Zahlenrätsel
• Altersrätsel
• Aus der Geometrie
• Verteilungsaufgaben
• Wissenstest

Mathematik-digital.de

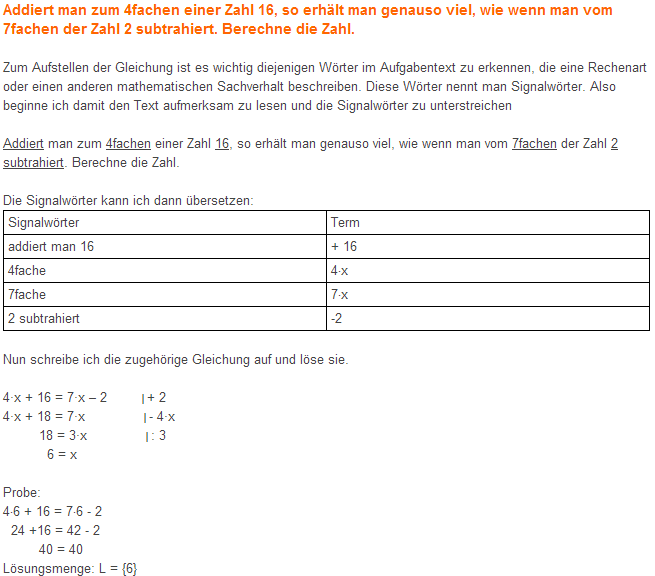
Zahlenrätsel gehören zu den leichtesten Textaufgaben, dass sagen zumindest die Mathematiker. Siehst du das genauso?

Sieh dir mal das folgende Beispiel an und entscheide dann selbst ...

Einführung

In diesem Kapitel kannst du lernen, wie man den Text einer Aufgabe in die Sprache der Mathematik, also in eine Gleichung, übersetzt und dadurch das Rätsel lösen kann.

Schreibe nun den Merktext in dein Übungsheft!

Merke

1. Lies den Aufgabentext aufmerksam durch.
2. Unterstreiche die Signalwörter.
3. Schreib die Signalwörter heraus und übersetze sie.
4. Stelle die zur Aufgabe gehörige Gleichung auf.
5. Löse die Gleichung, mache die Probe und schreibe eine Antwort.

Anfänger

Übung

Übersetze in die Sprache der Mathematik, indem du die Aussagen und passenden Terme einander zuordnest. Wenn du alle Terme zugeordnet hast, kannst du deine Lösung überprüfen lassen.

Multipliziere 12 mit der Summe von a und 6.	12*(a+6)	12a+72
Die Differenz von a und 8 wird durch 7 dividiert.	(a-8)/7	a/7-8/7
Die Summe von a und b ist zu verdoppeln.	(a+b)*2	2a+2b
Vermindere das Produkt von a und b um die Summe von x und y.	ab-(x+y)	ab-x-y

Aufgabe

Löse die folgenden Zahlenrätsel in deinem Heft und füge die Lösungszahl in das Kästchen.

Das Doppelte einer natürlichen Zahl vermindert um 3 ergibt 11. Wie heißt die Zahl? 7 ()

Addiert man zum Fünffachen einer Zahl die Hälfte dieser Zahl, so erhält man dasselbe, wie wenn man 5 zu dieser Zahl zählt und das Ergebnis verdreifacht. 6 ()

Durch welche Zahl muss man 80,08 dividieren, um 8,8 zu erhalten? 9,1 ()

Die Summe zweier Zahlen ist 37. Die erste Zahl ist um 9 größer als die zweite Zahl. 14 ()

Fortgeschrittene

Übung

Löse die Textaufgaben in deinem Heft und fülle die Lücken richtig aus!

• Die Wohnung A hat um zwei Zimmer mehr als die Wohnung B. Die passende Gleichung lautet A-2=B.

Die Wohnung B hat doppelt so viele Zimmer wie die Wohnung A.
Dieser Zusammenhang in Form einer Gleichung lautet 2A=B.

• Das Dreifache einer Zahl ist um 2 kleiner als die Differenz aus dem Fünffachen der Zahl und 8.
  Die Zahl lautet x=5.

• Welche Zahl ergibt mit 2/3 multipliziert ebenso viel wie wenn man sie um 2/3 vermindert? Die Lösung lautet x=2.

• Von drei Zahlen ist die Erste dreimal so groß wie die Zweite, die Dritte ist um 4 größer als die Erste. Wenn ihre Summe 480 ist,lauten die Zahlen x=68, y=204 und z=208. (kleinste Lösung zuerst!)

• Die Falschen Antworten sind: A+2=B, A=2B, x=2,5 und x=198

Aufgabe

Christiano R. möchte für seinen Klub ebenso viele Tore schießen wie im letzten Jahr. Er erzielte im letzten Jahr um 2 Tore mehr als im vorletzten Jahr und sogar um 5 Tore mehr als vor drei Jahren. Insgesamt brachte er es in den drei Saisonen auf 41 Tore.

Wie viel Tore hat Christiano im letzten Jahr geschossen? (16 Tore) (!11 Tore) (!14 Tore) (!12 Tore)

Experten

Aufgabe

Löse die folgenden Textaufgaben in deinem Übungsheft.

Multipliziert man eine Zahl mit ihrem Nachfolger, so erhält man das gleiche,
wie wenn man die um 6 kleiner Zahl mit der um 6 größeren Zahl multipliziert.
Wie heißt die Zahl?

Die Zahl lautet: -36

Die Zahl 88 soll so in zwei Teile geteilt werden,
dass der Unterschied ihrer Quadrate 880 ergibt.

Die Zahl 88 muss in 39 und 49 geteilt werden.

Übung

Löse die Textaufgaben unter Berücksichtigung des Stellenwertes. Arbeite in deinem Heft.

In einer dreiziffrigen Zahl ist die Hunderterziffer um 1 größer als die Zehnerziffer, die Einerziffer um 3 kleiner als die Zehnerziffer. Vertauscht man die Hunderterziffer mit der Einerziffer, dann ist die neue Zahl um 70 kleiner als die Hälfte der Ausgangszahl. Wie lautet die Ausgangszahl?652()

Eine zweiziffrige Zahl hat die Ziffernsumme 6. Vertauscht man die Ziffern, so ist die neu entstandene Zahl um 6 größer als das Dreifache der ersten Zahl. Wie heißt die Zahl? 15 ()

Weiter