Terme/Umformen von Termen: Unterschied zwischen den Versionen
Main>Walla Marina K (→Übungsaufgaben) |
Keine Bearbeitungszusammenfassung |
||
| (21 dazwischenliegende Versionen von 9 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Lernpfad Terme}}|Lernschritte einblenden|Lernschritte ausblenden}} | |||
__NOTOC__ | |||
==Äquivalente Terme== | |||
{{Box|1=Aufgabe|2=Übertrage die Zeichnung in dein Heft und überlege dir zwei verschiedene Terme, mit denen du den Flächeninhalt der <span style="color: green">grün</span> markierten Fläche ausrechnen kannst. (Hinweis: <math>b_1 = b_2 = b </math>) | |||
Tipp: In der vorherigen Aufgabe gab es auch 2 Möglichkeiten den Flächeninhalt zu errechnen. | Tipp: In der vorherigen Aufgabe gab es auch 2 Möglichkeiten den Flächeninhalt zu errechnen. | ||
[[Bild:einstieg_addierensubtrahieren_neu.jpg]] | |||
{{Lösung versteckt|1= | |||
1. Möglichkeit: Man rechnet den Flächeninhalt des gesamten Rechtecks aus 2b•4 und zieht den Flächeninhalt des kleinen Rechtecks 2b ab. Also: | 1. Möglichkeit: Man rechnet den Flächeninhalt des gesamten Rechtecks aus 2b•4 und zieht den Flächeninhalt des kleinen Rechtecks 2b ab. Also: <math> A_1(b)= 2b \cdot 4-2b </math> | ||
2. Möglichkeit: Man rechnet den Flächeninhalt eines kleinen Rechtecks aus 2b und nimmt ihn mal drei. Also | 2. Möglichkeit: Man rechnet den Flächeninhalt eines kleinen Rechtecks aus 2b und nimmt ihn mal drei. Also <math> A_2(b)= 3 \cdot 2b </math> | ||
Bei jeder Einsetzung für b müssen die beiden unterschiedlich aussehenden Terme dasselbe Ergebnis ergeben, weil es lediglich verschiedene Rechenwege zur Berechnung des gleichen Flächeninhalts sind. Diese Terme sind <u>'''gleichwertig'''</u>. | Bei jeder Einsetzung für b müssen die beiden unterschiedlich aussehenden Terme dasselbe Ergebnis ergeben, weil es lediglich verschiedene Rechenwege zur Berechnung des gleichen Flächeninhalts sind. Diese Terme sind <u>'''gleichwertig'''</u>. | ||
}} | |||
|3=Arbeitsmethode}} | |||
===Erklärung=== | |||
Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen, heißen <u>'''gleichwertig'''</u> oder <u>'''äquivalent'''</u>. | Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen, heißen <u>'''gleichwertig'''</u> oder <u>'''äquivalent'''</u>. | ||
Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen. | Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen. | ||
<u>Rechengesetze:</u> | |||
{|width="99%" | {| width="99%" | ||
|width="40%" style="vertical-align:top"| | | width="40%" style="vertical-align:top" | | ||
* '''Kommutativgesetz (KG)''': für alle rationalen Zahlen a, b gilt: | *'''Kommutativgesetz (KG)''': für alle rationalen Zahlen a, b gilt: | ||
::a+b = b+a | |||
:: | ::<math>a+b = b+a</math> | ||
* '''Assoziativgesetz (AG)''': für alle rationalen Zahlen a, b, c gilt: | ::<math>a \cdot b = b \cdot a</math> | ||
::a+(b+c) = (a+b)+c = a+b+c | |||
:: | *'''Assoziativgesetz (AG)''': für alle rationalen Zahlen a, b, c gilt: | ||
* '''Distributivgesetz (DG)''': für alle rationalen Zahlen a, b, c gilt: | |||
:: | ::<math>a+(b+c) = (a+b)+c = a+b+c</math> | ||
::<math>a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c</math> | |||
*'''Distributivgesetz (DG)''': für alle rationalen Zahlen a, b, c gilt: | |||
::<math>a \cdot (b+c) = a \cdot b+a \cdot c</math> | |||
:für alle rationalen Zahlen a, b, c (a<math>\neq</math> 0) gilt: | :für alle rationalen Zahlen a, b, c (a<math>\neq</math> 0) gilt: | ||
::(b+c):a = b:a+c:a | ::<math>(b+c):a = b:a+c:a</math> | ||
|width="50%" style="vertical-align:top"| | | width="50%" style="vertical-align:top" | | ||
|width="70%" style="vertical-align:center"| | | width="70%" style="vertical-align:center" | | ||
[[Bild:erklärwurm.gif]] | [[Bild:erklärwurm.gif]] | ||
|} | |} | ||
===Beispiel=== | |||
< | |||
T(a;b)= 3a+(7b+2a) | |||
{{Box|1=Übung|2= | |||
<math>T(a;b)= 3a+(7b+2a) </math> | |||
<math>\overset{(KG)}{= } 3a+(2a+7b) </math> | |||
<math>\overset{(AG)}{= } (3a+2a)+7b </math> | |||
<math>= 5a+7b </math> | |||
Durch geschicktes Anwenden der Rechengesetze kannst du einen Term zu einem äquivalenten Term vereinfachen. | Durch geschicktes Anwenden der Rechengesetze kannst du einen Term zu einem äquivalenten Term vereinfachen. | ||
Vereinfache nun selbst folgende Terme: | Vereinfache nun selbst folgende Terme: | ||
a)T(a;b)= 7a+(9b+6a) | a) <math> T(a;b)= 7a+(9b+6a) </math> | ||
{{Lösung versteckt|1= | |||
a) <math> T(a;b)= 7a+(9b+6a) </math> | |||
<math>\overset{(KG)}{= } 7a+(6a+9b) </math> | |||
<math>\overset{(AG)}{= } (7a+6a)+9b </math> | |||
<math>= 13a+9b </math> | |||
<br> | |||
}} | |||
b) <math> T(a;b)= 2 \cdot (a \cdot 3) \cdot b+4 \cdot (a \cdot 5) \cdot b </math> | |||
{{Lösung versteckt|1= | |||
b) <math> T(a;b)= 2 \cdot (a \cdot 3) \cdot b+4 \cdot (a \cdot 5) \cdot b </math> | |||
<math> \overset{(KG)}{= } 2 \cdot (3 \cdot a) \cdot b+4 \cdot (5 \cdot a) \cdot b </math> | |||
<math> \overset{(AG)}{= } (2 \cdot 3) \cdot a \cdot b+(4 \cdot 5) \cdot a \cdot b </math> | |||
<math> = 6ab+20ab </math> | |||
< | <math> = 26ab </math> | ||
<br | <br> | ||
}} | |||
c) <math> T(x)= (3+5 \cdot x) \cdot x </math> | |||
< | |||
{{Lösung versteckt|1= | |||
</ | c) <math> T(a;b)= (3+5 \cdot x) \cdot x </math> | ||
< | |||
< | <math> \overset{(DG)}{= } 3 \cdot x+5 \cdot x \cdot x </math> | ||
{| | |||
| | <math> = 3x+5x^2</math> | ||
Gleichartige Glieder werden addiert, indem man die | <br> | ||
::< | }} | ||
|3=Üben}} | |||
==Addieren und Subtrahieren äquivalenter Termglieder== | |||
{{Box|1=Augaben|2=Überlege, ob du folgende Terme vereinfachen kannst: | |||
*<math> 5 \cdot x+3 \cdot x= </math> | |||
{{Lösung versteckt|1= | |||
<math>5 \cdot x+3 \cdot x= 8 \cdot x=8x </math> | |||
<br> | |||
}} | |||
*<math>5 \cdot x-3 \cdot x= </math> | |||
{{Lösung versteckt|1= | |||
<math>5 \cdot x-3 \cdot x= 2 \cdot x= 2x </math> | |||
<br> | |||
}} | |||
|3=Arbeitsmethode}} | |||
===Erklärung:=== | |||
{{Box|1=Zusammenfassen mit Hilfe des Distributivgesetzes|2= | |||
Gleichartige Glieder werden addiert, indem man die Koeffizienten addiert und die gemeinsame Variable beibehält: | |||
::<math>m \cdot x + n \cdot x = ( m+n ) \cdot x </math> | |||
Gleichartige Glieder werden subtrahiert, indem man vom Koeffizienten des Minuenden den Koeffizienten des Subtrahenden subtrahiert und die gemeinsame Variable beibehält: | Gleichartige Glieder werden subtrahiert, indem man vom Koeffizienten des Minuenden den Koeffizienten des Subtrahenden subtrahiert und die gemeinsame Variable beibehält: | ||
::< | ::<math> m \cdot x - n \cdot x = ( m-n ) \cdot x </math> | ||
| | |||
| | {{Lösung versteckt|1='''Koeffizient''' | ||
|} | Ein Koeffizient ist eine reelle Zahl, die mit einer Variable multipliziert wird. | ||
zum Beispiel: | |||
3x+4y | |||
hier sind 3 und 4 Koeffizienten|2=Definition Koeffizienten|3=Definition ausblenden}} | |||
|3=Merksatz}} | |||
{{Box|1=Übung|2= | |||
<math> T(x)= 9 \cdot x-6+7 \cdot x+8 = 9x+7x-6+8 = 16x+2 </math> | |||
< | |||
<br />Um einen Term übersichtlicher zu machen, solltest du die Teilterme nach dem Alphabet ordnen und dann die Teilterme mit gleicher Variable zusammenfassen.<br /> | <br />Um einen Term übersichtlicher zu machen, solltest du die Teilterme nach dem Alphabet ordnen und dann die Teilterme mit gleicher Variable zusammenfassen.<br /> | ||
Fasse nun selbst folgende Terme so weit wie möglich zusammen: | Fasse nun selbst folgende Terme so weit wie möglich zusammen: | ||
* T(z)= | * <math> T(z)= 8 \cdot z^2-7+3 \cdot z+(4 \cdot z^2+2 \cdot z^2)-2z </math> | ||
{{Lösung versteckt|1= | |||
<math> T(z)= 8 \cdot z^2-7+3 \cdot z+(4 \cdot z^2+2 \cdot z^2)-2z = </math> | |||
< | |||
<math>= 8z^2-7+3z+6z^2-2z = </math> | |||
<math>= 8z^2+6z^2+3z-2z-7 = </math> | |||
<math>= 14z^2+z-7 </math> | |||
<br> | |||
}} | |||
* <math> T(n)= 2,2 \cdot n+2,8 \cdot n^2-0,25+ \left[ n(2,7+0,3n)\right]</math> | |||
{{Lösung versteckt|1= | |||
< | <math> T(n)= 2,2 \cdot n+2,8 \cdot n^2-0,25+ \left[ n(2,7+0,3n)\right] = </math> | ||
T( | <math> = 2,2n+2,8n^2-0,25+ \left[ 2,7n+0,3n^2)\right] = </math> | ||
< | |||
T( | <math> = 2,2n+2,8n^2-0,25+2,7n+0,3n^2 = </math> | ||
<math> = 2,8n^2+0,3n^2+2,2n+2,7n-0,25 = </math> | |||
<math> = 3,1n^2+4,9n-0,25 </math> | |||
<br> | |||
</ | }} | ||
< | |||
< | * <math> T(a;b)= 4a^2-2a+3b+2-8b^2+a(2b+9) </math> | ||
| | {{Lösung versteckt|1= | ||
<math> T(a;b)= 4a^2-2a+3b+2-8b^2+a(2b+9) = </math> | |||
<math>= 4a^2-2a+3b+2-8b^2+2ab+9a = </math> | |||
<math>= 4a^2-2a+9a+2ab-8b^2+3b+2 = </math> | |||
<math>= 4a^2+7a+2ab-8b^2+3b+2 </math> | |||
<br> | |||
}} | |||
|3=Üben}} | |||
==Multiplizieren eines Produkts mit einer Zahl und Dividieren eines Produkts durch eine Zahl== | |||
{{Box|1=Aufgabe|2=Überlege, wie du mit Hilfe der Rechengesetze den folgenden Term vereinfachen kannst. | |||
<math> T(x)= (3 \cdot a) \cdot 2 </math> | |||
{{Lösung versteckt|1= | |||
<math>T(x)= (3 \cdot a) \cdot 2= </math> | |||
<math> \overset{(AG)}{= } 3 \cdot (a \cdot 2) = </math> | |||
<math> \overset{(KG)}{= } 3 \cdot (2 \cdot a) = </math> | |||
<math> \overset{(AG)}{= } (3 \cdot 2) \cdot a = </math> | |||
<math> = 6 \cdot a </math> | |||
<math> = 6a</math> | |||
<br> | |||
}} | |||
|3=Arbeitsmethode}} | |||
===Erklärung=== | |||
{{Box|1=Kommutativ- und Assoziativgesetz kombiniert|2= | |||
Man multipliziert ein Produkt mit einer Zahl, indem man '''einen''' der Faktoren mit dieser Zahl multipliziert. | Man multipliziert ein Produkt mit einer Zahl, indem man '''einen''' der Faktoren mit dieser Zahl multipliziert. | ||
: | :<math> ( 4 \cdot a ) \cdot 3 = 4 \cdot (a \cdot 3) = 4 \cdot ( 3 \cdot a) = ( 4 \cdot 3 ) \cdot a = 12 \cdot a = 12a </math>|3=Merksatz}} | ||
| | |||
{{Box|1=Übung|2= | |||
Überlege nun, wie du folgenden Term vereinfachen kannst. | Überlege nun, wie du folgenden Term vereinfachen kannst. | ||
T(a)= ( | <math> T(a)= (14 \cdot a):2 </math> | ||
< | {{Lösung versteckt|1= | ||
T(a)= ( | <math> T(a)= (14 \cdot a)/2 = </math> | ||
<math> = \frac{14 \cdot a}{2} </math> | |||
<math> = \frac{7 \cdot a}{1} </math> | |||
<math> = 7 \cdot a </math> | |||
<math> = 7a </math> | |||
<br> | |||
}} | |||
|3=Üben}} | |||
===Erklärung=== | |||
{{Box|1=Kommutativ- und Assoziativgesetz kombiniert|2= | |||
{| | |||
| | |||
Man dividiert ein Produkt durch eine Zahl, indem man '''einen''' der Faktoren durch diese Zahl dividiert. | Man dividiert ein Produkt durch eine Zahl, indem man '''einen''' der Faktoren durch diese Zahl dividiert. | ||
</ | : <math> ( 9*a ) : 3 = \frac{9*a}{3} = \frac{3*a}{1} = 3 \cdot a = 3a </math>|3=Merksatz}} | ||
{{Box|1=Übung|2=Forme möglichst einfache Terme: | |||
* <math> (-6n):2 </math> | |||
* <math> 24 \cdot 0,5b </math> | |||
* <math> 2m \cdot 6 </math> | |||
* <math> 25y:(-0,1) </math> | |||
* <math> \left( \frac{x}{4} +\frac{x}{12} \right) :3 </math> | |||
* <math> (2y+5y-6y) \cdot 2 </math> | |||
{{Lösung versteckt|1= | |||
* <math> (-6n):2= \frac{-6n}{2} = \frac{-3n}{1} = -3n </math> | |||
* <math> 24 \cdot 0,5b= (24 \cdot 0,5) \cdot b= 12 \cdot b= 12b </math> | |||
* <math> 2m \cdot 6= (2 \cdot 6) \cdot m= 12 \cdot m= 12m </math> | |||
* <math> 25y:(-0,1)= \frac{25y}{-0,1} = \frac{-250y}{1} = -250y </math> | |||
* <math>\left( \frac{x}{4} +\frac{x}{12} \right) :3 = \left( \frac{3x}{12} +\frac{x}{12}\right) :3 = \left( \frac{4x}{12}\right) :3 = \left( \frac{x}{3}\right) :3 = \frac{x}{3} *\frac{1}{3} = \frac{x}{9} </math> | |||
* <math> (2y+5y-6y) \cdot 2= y \cdot 2= 2y </math> | |||
}} | |||
|3=Üben}} | |||
==Übungsaufgaben== | |||
{{Box|1=Aufgabe 1|2= | |||
Prüfe, ob die Terme äquivalent sind | Prüfe, ob die Terme äquivalent sind | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
<big>''' 1: '''</big> | <big>''' 1: '''</big> | ||
<math> T_1(x)= 5x-2x+6x </math> | |||
<math> T_2(x)= 2 \cdot x \cdot 2+5x</math> | |||
(äquivalent) (!nicht äquivalent) | (äquivalent) (!nicht äquivalent) | ||
<big>''' 2 : '''</big> | <big>''' 2 : '''</big> | ||
<math> T_1(y)= 4y-3 \cdot 4y+15</math> | |||
<math> T_2(y)= 3 \cdot 5+2y-4y-6y</math> | |||
( | (äquivalent) (!nicht äquivalent) | ||
<big>''' 3: '''</big> | <big>''' 3: '''</big> | ||
<math> T_1(y;z)= 2y-3+z</math> | |||
<math> T_2(y;z)= 5y \cdot 2+z+5-8y-8</math> | |||
(äquivalent) (!nicht äquivalent) | (äquivalent) (!nicht äquivalent) | ||
| Zeile 252: | Zeile 300: | ||
<big>''' 4: '''</big> | <big>''' 4: '''</big> | ||
<math> T_1(z)= 4 \cdot\frac{3}{2} -2z </math> | |||
<math> T_2(z)= 6+8z-5 \cdot 20%-z \cdot 9</math> | |||
(!äquivalent) (nicht äquivalent) | (!äquivalent) (nicht äquivalent) | ||
| Zeile 260: | Zeile 308: | ||
<big>''' 5: '''</big> | <big>''' 5: '''</big> | ||
<math> T_1(r)= 3r-2^3 r+5-r </math> | |||
<math> T_2(r)= 3 \cdot r \cdot 2 </math> | |||
(!äquivalent) (nicht äquivalent) | (!äquivalent) (nicht äquivalent) | ||
</div> | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Aufgabe 2|2= | |||
Wie ändert sich der Flächeninhalt eines Dreiecks, wenn man seine Grundseite c verdoppelt und die dazugehörige Höhe h<sub>c</sub> verdreifacht? | Wie ändert sich der Flächeninhalt eines Dreiecks, wenn man seine Grundseite c verdoppelt und die dazugehörige Höhe h<sub>c</sub> verdreifacht? | ||
{{Lösung versteckt|1= | |||
<math> A = \frac{1}{2} \cdot c \cdot h_c </math><br /> | |||
<math> A _{neu} = \frac{1}{2} \cdot 2 \cdot c \cdot 3 \cdot h_c = \frac{1}{2} \cdot c \cdot h_c \cdot 2 \cdot 3 = \frac{1}{2} \cdot c \cdot h_c \cdot 6 = A \cdot 6 = 6A </math> | |||
Der Flächeinhalt des Dreiecks versechsfacht sich. | Der Flächeinhalt des Dreiecks versechsfacht sich. | ||
}} | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Aufgabe 3|2= | |||
Finde heraus, welcher der beiden unteren Terme jeweils der äquivalente zum oberen, ursprünglichen Term ist. Notiere die Buchstaben hinter der richtigen Lösung und überprüfe dein Lösungswort. | Finde heraus, welcher der beiden unteren Terme jeweils der äquivalente zum oberen, ursprünglichen Term ist. Notiere die Buchstaben hinter der richtigen Lösung und überprüfe dein Lösungswort. | ||
{{{!}} class="wikitable center" | |||
{{!}}- | |||
! ursprünglicher Term !! <math> 3x+2x^2-x+3x^2 </math> !! <math> 7x+x </math> !! <math> x^3-x^2+2x^3 </math> !! <math> x \cdot x \cdot x </math> !! <math> x+x-2x </math> !! <math>x-2x </math> !! <math> x+x+3x^2 </math> | |||
{{!}}- | |||
{{!}} 1.Vorschlag {{!}}{{!}} <math> 5x^2+2x [S] </math> {{!}}{{!}} <math> 7x^2 [E] </math> {{!}}{{!}}<math> x+2x^3 [H] </math> {{!}}{{!}} <math> x^3 [T] </math> {{!}}{{!}} <math> 0 [Z] </math> {{!}}{{!}} <math> -x [E] </math> {{!}}{{!}} <math> 3x^4 [?] </math> | |||
{{!}}- | |||
{{!}} 2.Vorschlag {{!}}{{!}} <math> 6x^4-3x^2 [F] </math> {{!}}{{!}} <math> 8x [P] </math> {{!}}{{!}} <math> 3x^3-x^2 [I] </math> {{!}}{{!}} <math> 3x [L] </math> {{!}}{{!}} <math> x^2-2x [E] </math> {{!}}{{!}} <math> -2x^2 [R] </math> {{!}}{{!}} <math> 2x+3x^2 [!] </math> | |||
{{!}}- | |||
{{!}}} | |||
{| | {{Lösung versteckt|SPITZE!|Lösungswort|Lösungswort verbergen}} | ||
! | |3=Arbeitsmethode}} | ||
| | |||
| | |||
| | |||
[[ | {{Fortsetzung|weiter=Auflösen von Klammern|weiterlink=../Auflösen von Klammern}} | ||
[[Kategorie:Variable]] | |||
[[Kategorie:Terme]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 16:02 Uhr
Äquivalente Terme
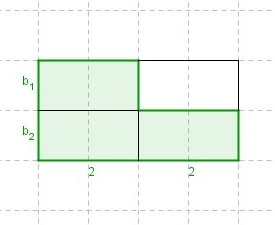
Übertrage die Zeichnung in dein Heft und überlege dir zwei verschiedene Terme, mit denen du den Flächeninhalt der grün markierten Fläche ausrechnen kannst. (Hinweis: )
Tipp: In der vorherigen Aufgabe gab es auch 2 Möglichkeiten den Flächeninhalt zu errechnen.
1. Möglichkeit: Man rechnet den Flächeninhalt des gesamten Rechtecks aus 2b•4 und zieht den Flächeninhalt des kleinen Rechtecks 2b ab. Also:
2. Möglichkeit: Man rechnet den Flächeninhalt eines kleinen Rechtecks aus 2b und nimmt ihn mal drei. Also
Bei jeder Einsetzung für b müssen die beiden unterschiedlich aussehenden Terme dasselbe Ergebnis ergeben, weil es lediglich verschiedene Rechenwege zur Berechnung des gleichen Flächeninhalts sind. Diese Terme sind gleichwertig.Erklärung
Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen, heißen gleichwertig oder äquivalent. Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen.
Rechengesetze:
|
Beispiel
Durch geschicktes Anwenden der Rechengesetze kannst du einen Term zu einem äquivalenten Term vereinfachen. Vereinfache nun selbst folgende Terme:
a)
a)
b)
b)
c)
c)
Addieren und Subtrahieren äquivalenter Termglieder
Überlege, ob du folgende Terme vereinfachen kannst:
Erklärung:
Gleichartige Glieder werden addiert, indem man die Koeffizienten addiert und die gemeinsame Variable beibehält:
Gleichartige Glieder werden subtrahiert, indem man vom Koeffizienten des Minuenden den Koeffizienten des Subtrahenden subtrahiert und die gemeinsame Variable beibehält:
Koeffizient
Ein Koeffizient ist eine reelle Zahl, die mit einer Variable multipliziert wird.
zum Beispiel: 3x+4y
hier sind 3 und 4 Koeffizienten
Um einen Term übersichtlicher zu machen, solltest du die Teilterme nach dem Alphabet ordnen und dann die Teilterme mit gleicher Variable zusammenfassen.
Fasse nun selbst folgende Terme so weit wie möglich zusammen:
Multiplizieren eines Produkts mit einer Zahl und Dividieren eines Produkts durch eine Zahl
Überlege, wie du mit Hilfe der Rechengesetze den folgenden Term vereinfachen kannst.
Erklärung
Man multipliziert ein Produkt mit einer Zahl, indem man einen der Faktoren mit dieser Zahl multipliziert.
Überlege nun, wie du folgenden Term vereinfachen kannst.
Erklärung
Man dividiert ein Produkt durch eine Zahl, indem man einen der Faktoren durch diese Zahl dividiert.
Forme möglichst einfache Terme:
Übungsaufgaben
Prüfe, ob die Terme äquivalent sind
1:
(äquivalent) (!nicht äquivalent)
2 :
(äquivalent) (!nicht äquivalent)
3:
(äquivalent) (!nicht äquivalent)
4:
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle T_2(z)= 6+8z-5 \cdot 20%-z \cdot 9}
(!äquivalent) (nicht äquivalent)
5:
(!äquivalent) (nicht äquivalent)
Wie ändert sich der Flächeninhalt eines Dreiecks, wenn man seine Grundseite c verdoppelt und die dazugehörige Höhe hc verdreifacht?
Finde heraus, welcher der beiden unteren Terme jeweils der äquivalente zum oberen, ursprünglichen Term ist. Notiere die Buchstaben hinter der richtigen Lösung und überprüfe dein Lösungswort.
| ursprünglicher Term | |||||||
|---|---|---|---|---|---|---|---|
| 1.Vorschlag | |||||||
| 2.Vorschlag |